关于数列最值问题的解法探究与建议
2020-09-26谢福慧
谢福慧
[摘 要] 数列最值问题是高考的常见问题类型之一,考虑到数列的函数本质,可以参考函数问题的解法来求解. 文章将对数列最值问题的背景加以剖析,结合实例探究单调性法、数形结合法、不等式法和导数法的解题技巧,并提出相应的教学建议.
[关键词] 数列;最值;单调性;数形结合;导数;不等式
问题背景
数列是一种定义在正整数集上的特殊函数,以数列为基础的最值问题是高中数学常见的问题类型,该类问题考点涉及数列性质、前n项和求法、最值内容、不等式、函数等. 从数列的函数属性来看,求解函数最值的方法同样适用于数列最值问题,故可利用单调性分析、数形结合、基本不等式、导数法等方法来加以求解. 对于数列最值问题的求解,可以归纳为“读题、建模、选法、求解、还原”十字,即第一步是理解问题中的条件和结论;第二步是用数学符号表述问题;建立相应的模型;第三步则是基于问题模型选定合适的解法;第四步对问题进行简化破解;第五步则是基于问题解来还原问题答案.
方法探究
求解数列最值的方法有很多,针对问题的特点需要选用合适的方法,下面结合实例探索不同方法的使用策略.
1. 单调性法
单调性法是数列问题的常用方法,包括数列的单调性和函数的单调性,基于内容性质求解时需要从不同的方向分析思考,尤其是利用函数单调性分析时需要结合数列结构来构建函数,然后进行性质分析,确定其最值.
例1:已知数列{an}的通项公式an=■(n∈N+),試求数列中最大的项.
分析:题干给出了数列的通项公式,求最大的项可从数列的通项公式入手,分析其形式构建相应的函数. 通项公式的分子和分母中均含有变量n,可以对其适度变形,可得an=■,显然当分母n+■取得最小值时,an可取得最大值.由分母形式可构建函数y=x+■(x>0),后续利用函数的性质求最值即可.
解:变形可得a■=■,联想函数y=x+■(x>0),可知函数在(0,■)上单调递减,在(■,+∞)上单调递增,显然当且仅当x=■时函数可取得最小值,结合n∈N+可知要确保n+■取得最小值,需使得n=[■],计算可知当n=12或13时,an最大,因此数列中最大的项为a12和a13.
评析:上述求解数列中最大的项时采用了函数单调性法,但在求解时有两点需要注意:一是构造函数时需要紧密结合通项公式的结构;二是充分考虑数列正整数集合的特性,利用函数单调性只可以确定最值数列项的贴近情形,还需进一步比对分析.
2. 数形结合法
数列是一种特殊的函数,函数具有“数”与“形”的双重特性,因此部分数列具有一定的几何意义,可以采用数形结合的方法来分析突破.求解时需要分两步进行:第一步推导数列的通项公式;第二步根据数列的通项对其图像进行研究.
例2:在正项等比数列{an}中,已知公比q∈(0,1),且a1a5+2a3a5+a2a8=25,a3与a5的等比中项为2.
(1)试求数列{an}的通项公式;
(2)设bn=log2an,Sn为数列{bn}的前n项之和,试求当■+■+…+■取得最大值时n的值.
分析:(1)根据题干的等量关系,以及公比的取值范围可以确定首项和公比的值;(2)数式中涉及数列的前n项之和,具有无穷性,需借助数列通项公式来分析数式的通性,需要关注数列中的“零”项,利用图像特性来分析最值情形.
解:(1)分析可知a1=16,q=■,则{an}的通项公式为an=25-n.
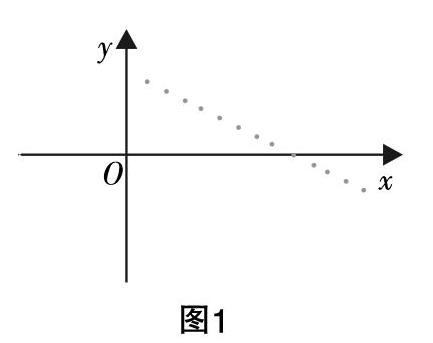
(2)bn=log2an=5-n,b1=bn+1-bn=-1,即{bn}是以b1=4为首项、以-1为公差的等差数列,则其前n项之和Sn=■,则■=■,可将其视为关于正整数n的函数,散点图如图1所示. 由图像可知当n≤8时,■>0;当n=9时,■=0,;当n>9时,■<0,所以当n=8或9时,■+■+…+■取得最大值.
评析:等差数列可以视为关于n的一次函数,因此根据通项公式绘制相应的函数图像,直观呈现数列项的数值变化,从而分类提取其中的正数和负数,确定与数列项相关的数式最值. 另外需要关注数列中的“零”项,该特殊项是问题多解的因素之一.
3. 不等式法
求解数列最值问题同样可以采用不等式法,利用不等式的性质分析,也可以利用不等式的放缩技巧. 不等式的性质较为众多,包括对称性、传递性和运算规律等,需灵活运用.
例3:已知函数f(x)的解析式为f(x)=x2+(a+8)x+a2+a-12,且有f(a2-4)=f(2a-8),设等差数列{an}的前n项之和为Sn(n∈N+),如果Sn=f(n),试求■的最小值.
分析:■中的参数涉及等差数列{an}的要素,因此需要结合数列来对其加以分析,从而构建关于n的数式,最值分析可以直接借助基本不等式的性质.
解:函数f(x)=x2+(a+8)x+a2+a-12的对称轴为x=-■,由f(a2-4)=f(2a-8)可得a2-4=2a-8,或a2-4+2a-8=2·-■,则a=1或者a=-4,需要对其分类讨论:
当a=1时,f(x)=x2+9x-10,Sn=f(n)=n2+9n-10,a1=S1=0,a2=S2-S1=12,a3=S3-S2=14,a2-a1≠a3-a2,所以数列{an}不是等差数列,与题意不符,a=1舍去.
当a=-4时,f(x)=x2+4x,Sn= f(n)=n2+4n. 当n=1时,a1=S1=5;当n≥2时,an=Sn-Sn-1=2n+3,a1=5也满足,所以an=2n+3.
■=■=■×(n+1)+■+2≥■×2■+2=■+1,当且仅当n+1=■,即n=■-1时等号成立. 由于n始终为正整数,因此当n=3时原式可以取得最小值,且最小值为■.
评析:上述在求解数列前n项之和的最值时合理使用了均值不等式,均值不等式在代数类相关问题中有着广泛的应用,实际应用时可以灵活使用其简单结论:■≤■≤■≤■ (a,b∈R+).
4. 导数法
考虑到数列的函数特性,因此也可以采用导数法来求解数列最值问题. 求解时需要采用类比、联想构建的方式来建立中间函数,利用导函数的性质分析数列,从而求得最值.
例4:已知{an}为等差数列,Sn表示数列的前n项之和,若S10=0,S15=25,试求nSn的最小值.
分析:根据已知条件可以求得等差数列前n项之和为Sn=■n2-■n,所以nSn=■(n3-10n2),可据此构造函数f(x),利用导数法来分析f(n)的性质,从而确定其最小值.
解:根据题意易得Sn=■n2-■n,则nSn=■(n3-10n2)= f(n). 设f(x)=■(x3-10x2),x≥1. 其导函数f ′(x)=■(3x2-20x)=■x(3x-20). 令f ′(x)=0,則x=■. 分析可知当1
评析:上述在求解数列最值问题时采用了导数法,分两步进行:第一步基于数列通式构建与其相关的函数;第二步利用导函数的性质来把握数列的变化趋势,确定最值情形. 函数构造的方法有很多,数列问题中主要采用特征法,即根据数列的特征结构来联想构造函数.
教学思考
上述基于数列的本质属性呈现了最值问题的四种常用解法,并结合实例探究了问题的突破思路,下面结合教学实践提出几点建议.
1. 强化基础知识,注重知识关联
数列是高中数学的重点内容,需要总结常见数列的定义、性质以及前n项和的常用方法等,这些知识是求解数列最值问题的基础. 教学中需要引导学生对知识点进行整合,采用对比归纳的方式来构建数列内容的知识网络. 同时数列与函数、不等式等内容联系紧密,因此教学中还应注重数列的知识关联,帮助学生理清知识脉络,构建完整的知识体系.知识关联的方式有很多,可以结合综合性较强的问题,以一题为引入,引导学生提取题干信息的知识考点;也可以直接联系数列章节的前后知识,整合知识框图.
2. 关注问题属性,总结解题方法
数列是一种特殊的函数,因此具有函数的性质,同时也可以利用函数的研究方法和解题技巧来突破考题,因此在实际学习时需要从数列的本质属性出发,理解数列的相关定义,联系函数内容来总结解题方法. 本文所呈现的是数列最值问题的常用四种方法,其中单调性可用于研究数列的整体变化趋势,数形结合是建立在数列的几何意义之上的,不等式是从“数”的角度进行探究,导数法则是基于数列与函数的关联特性. 教学中需要教师从数列内容的本质属性入手,开展数列最值问题的解法归纳,总结特征问题的对应解法,形成系统的解题思路.
3. 重视思想方法,提升解题思维
开展解题方法教学是提升学生能力的重要方式,教学中不仅需要重视解题方法的讲解,还需要挖掘解法背后的思想. 例如上述问题的突破中涉及了数形结合思想、化归转化思想、方程思想、构造思想等,正是基于核心思想才完成了解法思路的构建. 因此开展数列最值问题的解法探究,需要融合数学思想,引导学生理解数学思想的内涵. 由于数学思想理解起来存在一定的困难,故可以结合教材内容、例题讲解,使学生初步掌握利用数学思想分析问题的步骤,在此基础上进行考题拓展,逐步提升学生思维的灵活性.
