量不在多，典型就行；题不在难，有变则灵

陈浩文 莫弘

[摘  要] “一题多解”正是帮助学生体会“通性通法”、学会总结提升的重要手段之一. 文章选择有多种解法并且解法具有代表性的习题进行探讨.

[关键词] 高中数学;解题教学;一题多解

新课程的理念要求“突出学生的主体地位”，具体体现在：教学是否有利于激发学生的学习兴趣，是否有利于学生积极主动地参与教学，是否有利于学生学习后能灵活地运用知识. 高中数学课程标准要求加强动手实践、自主探索、合作交流等学习方式，是一场学习上的改革. 数学教学是教师与学生之间相互交流、共同发展的过程，数学教学应该从学生的实际出发，通过创设有利于学生自主学习的问题情境，引导学生通过思考、探索、交流、实践来获得知识.

习题教学，对知识的复习、方法的提炼、数学思想的形成等方面的效果有着重要影响，如何选择问题及讲授问题就显得尤为重要，选择有多种解法并且解法具有代表性的习题进行教学，可以达到事半功倍的效果. 下面，以两个案例为例进行说明.

案例（一）：一道关于圆的问题

1. 例题展示

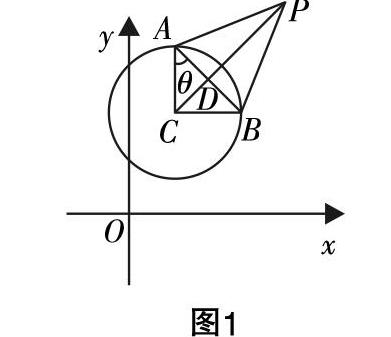
已知圆C：（x-1）2+（y-2）2=2，若等边三角形PAB的一边AB为圆C的一条弦，则PC的最大值为________.

【解法1】

如图1：连接AC，BC，设∠CAB=θ，连接PC，与AB交于点D，因为AC=BC，△PAB是等边三角形，所以D是AB的中点，所以PC⊥AB，所以圆C：（x-1）2+（y-2）2=2中，半径为■，AD=■cosθ，CD=■sinθ.

所以在等边三角形PAB中，PD=■AB=■cosθ，所以PC=CD+PD=■sinθ+■cosθ=2■·sinθ+■≤2■.

分析：考虑到问题是求最值，从角度的方面进行考虑，利用一个角将问题中涉及的线段表示出来，最后利用三角函数的有界性解决问题.这是对解三角形问题的复习和提升.

【解法2】

设AD=x，x∈（0，■]，则PC=■x+■，记f（x）=■x+■，则f′（x）=■-■.

令f′（x）=0，得x=■∈（0，■].当x∈0，■时，f′（x）≥0;当x∈■，■时，f′（x）<0，所以f（x）max=f■=2■.

分析：解法二是利用函数的单调性来解决问题，用一条边作为未知数将所求边表示出来，最后通过导数确定函数的单调性求出最值，这是解决最值问题的一般思想，也是函数思想在解决数学问题中的应用，具有一般性思维.

【解法3】

设AD=x，x∈（0，■]，则PC=■x+■，记y=■x+■.

设x=■sinθ，θ∈0，■，则y=■sinθ+■cosθ=2■sinθ+■≤2■.

分析：解法三与解法二类似，都是利用函数思想将所求边表示出来，在最后求最值时，根据函数解析式特点，利用三角代换的方法求函数的最值，体现了三角函数有界性的应用.

【解法4】

设AD=x，x∈（0，■]，则PC=■x+■，

则PC2=（■x+1×■）2≤[（■）2+12]·[x2+（■）2]=4×2=8.当且仅当■=■时取等号，PC≤2■，此时x=■.

分析：解法四同样利用了函数思想，求最值时使用了柯西不等式，体现了不等式在最值问题中的应用.

【解法5】

设AD=x，x∈（0，■]，则PC=■x+■，记f（x）=■x+■，x∈（0，■].

令u=■x，v=■得：u2=3x2，v2=2-x2，u2+3v2=6，即■+■=1.

令z=u+v，v=-u+z，问题转化为在条件■+■=1约束下，v=-u+z纵截距何时取最大值的问题.

当直线v=-u+z与椭圆■+■=1相切时，z最大，此时z=2■.

分析：函数思想再一次被使用，区别就是用换元法将问题转换为线性规划问题，求出最值. 这种方法难度较大，但是体现了线性规划是求最值问题的一种重要途径，对形成解题通法有一定的启发作用.

【解法6】

连接PC交AB于D，因为AB为圆的弦，△PAB为等边三角形，所以PC平分∠APB，∠APC=■，在△APC中，由正弦定理得：■=■，PC=■=■=2■sin∠PAC≤2■.

分析：解法六和解法一类似，直接利用解三角形的思想，将边化为角的形式，利用三角函数有界性求出最值.

2. 总结提升

这是一道中等难度的解三角形问题，一般来说，学生容易想到解法1和解法6，但是如果我们只满足解决问题，那么就会失去建立解题通法、提升数学思想的机会，所以教学时有必要挖掘解题方法，展示一题多解.

从这个问题的解决过程中，可以看到，求最值问题的核心思想在于函数思想，将所求量用其他变量表示出来，利用函数的性质求解.通过一题多解的教学，学生可以更充分地了解数学思想方法，也可以对求最值问题的具体知识和手段进行较为全面的复习，对各种知識方法进行比较，体会各种知识方法的异同，这对数学知识体系的构建有很大的推动作用.

案例（二）：一道关于双曲线离心率的问题

1. 例题展示

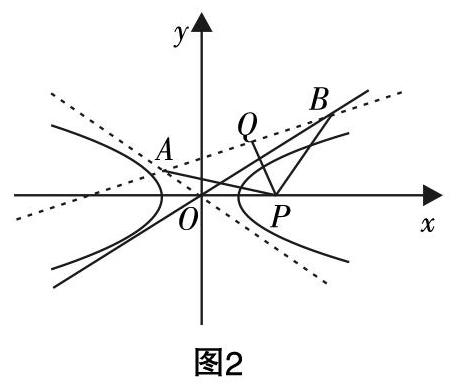
设直线x-3y+m=0（m≠0）与双曲线■-■=1？摇（a>0？摇，？摇b>0）的两条渐近线交于点A，B，若点P（m，0）满足PA=PB，则该双曲线的离心率是________.

【解法1】

渐近线方程为y=±■x，分别与x-3y+m=0联立，解得A■，■，B■，■，则AB的中点Q■，■. 如图2，因PA=PB，所以PQ⊥AB，kAB=■，所以kPQ=-3=■=■，解得2a2=8b2，所以e=■=■.

分析：解法1属于直接法，利用等腰三角形“三线合一”的性质，可知AB⊥PQ，由斜率关系求出a，b的关系.

【解法2】

双曲线的渐近线方程为y=±■x，渐近线与直线x-3y+m=0的交点的横坐标分别为■和■. 设AB的中点为Q，则点Q的横坐标为■. 又PQ的方程为3x+y-3m=0.

由方程组x-3y+m=0，3x+y-3m=0，可得点Q的横坐标为■m，则■=■m，解得a2=4b2，所以e=■.

【解法3】

设A（x1，y1），B（x2，y2），AB的中点Q（x0，y0），渐近线方程为■-■=0，即b2x2-a2y2=0，联立x-3y+m=0，b2x2-a2y2=0，得（9b2-a2）y2-6b2my+b2m2=0，则y0=■=■，x0=3y0-m=■，

则AB的中点Q■，■，同解法1.

分析：解法3整体代换，将两条渐近线看成二次曲线，并利用韦达定理直接求出点Q坐标.

【解法4】

设A（x1，y1）？摇，B（x2，y2），AB的中点Q（x0，y0），渐近线方程为■-■=0，即b2x2-a2y2=0，则b2x■-a2y■=0，b2x■-a2y■=0，两式相减得kAB·kOQ=■. 又kAB=■，所以■=■. 又PQ的方程为3x+y-3m=0，联立x-3y+m=0，3x+y-3m=0，得Q■，■，所以■=■=■=■，所以a2=4b2，所以e=■.

分析：解法4利用点差法，求出a，b的齐次关系式，再转化为所求的离心率.

【解法5】

令a=1，则渐近线方程为y=±bx，分别与x-3y+m=0联立，解得A■，■，B■，■，则AB的中点Q■，■. 因为kAB=■，所以kPQ=-3=■=■，解得2=8b2，所以c=■，所以e=■.

分析：解法5用特殊值法，令a=1，问题的本质并没有变化，运算会简单得多.

【解法6】

设A（x1，y1）？摇，？摇B（x2，y2），AB的中点Q（x0，y0），联立x-3y+m=0，3x+y-3m=0，得Q■，■，所以■=■=■.

因为渐近线方程为y=±■x，则y1=-■x1，y2=■x2，两式相减得y1-y2=-■（x1+x2），

两式相加得x1-x2=-■（y1+y2），所以有kAB=■=■=■. 又■=■=■，即■=■，所以a2=4b2，所以e=■.

分析：解法6设而不求，求出a，b的关系，再转化为所求的离心率.

2. 总结提升

这是一道典型的求圆锥曲线离心率的问题，主线思想在于“求离心率”就是要“找到a，b，c的等量关系”，而寻求等量关系的具体手段多种多样，习题教学就是应该突出主線，体现不同手段的差异性，帮助学生提炼数学思想方法，避免“见子打子”的教学和练习，真正达到提高效率的目的.

章建跃老师在《注重通性通法才是好数学教学》一文中提到：在“通性通法”中，“通性”就是概念所反映的数学基本性质;“通法”就是概念所蕴含的思想方法. 解题教学中，只有注重基础知识及其蕴含的数学思想方法，才是追求数学教学的“长期利益”. 这就要求我们努力提高对所教内容的理解水平，增强辨别和判断能力，对哪些重要哪些次要，哪些是根本哪些是细枝末节要心中有数，并在教学中培养学生联系基础、洞察本质的火眼金睛，这样才能落实数学课程的育人功能，使学生真正从“长期利益”中得到好处.

“一题多解”正是帮助学生体会“通性通法”、学会总结提升的重要手段之一. 关于解题，有一句话是这样说的：量不在多，典型就行，题不在难，有变则灵.让学生明确不能只寻求其解，还须以解题作为手段，去掌握知识和学会运用知识. 一题多解也是高考数学解答题的突出特征. 我们在平时的教学中，可以抓住问题中每一个可以作为“最近发展区”的点，引导学生从多方面考虑已知条件的不同数学表达，开拓思想，提高核心素养.