妙用托勒密定理,巧破截长补短法

文/深圳市龙岗区平湖实验学校 易泽健

在近几年的中考几何计算或证明中经常遇到线段间的数量关系问题：①a±b=c；②a+b=kc；③a+b=c+d(a,b,c表示线段，k表示常数)，一般的解题思路是截长补短法，本质是利用运用全等实现线段之间的等量代换，进而解决和差问题。无论是截长法还是补短法，都至少需要增加一条辅助线。辅助线的添加本身就是初中阶段图形证明题的一个难点，当学生多次尝试作辅助线都无法把思路打开时，可以尝试启用托勒密定理，化解“截长补短法”的思维障碍，体会数学学习带来的成就感。

1.托勒密定理

托勒密定理指出，圆内接凸四边形的两对相对边的乘积之和等于两条对角线的乘积.也就是说，如果圆是四边形ABCD的外接圆，则AC·BD=AB·CD+AD·BC。托勒密定理本质上是利用圆的性质，得出其中六条线段之间的数量关系。

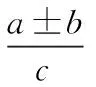
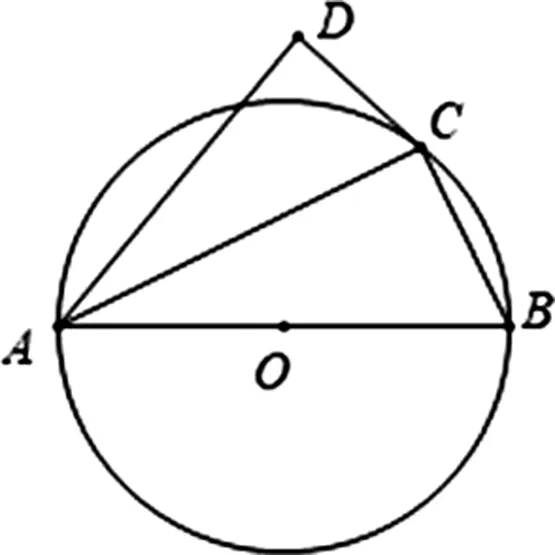
图1

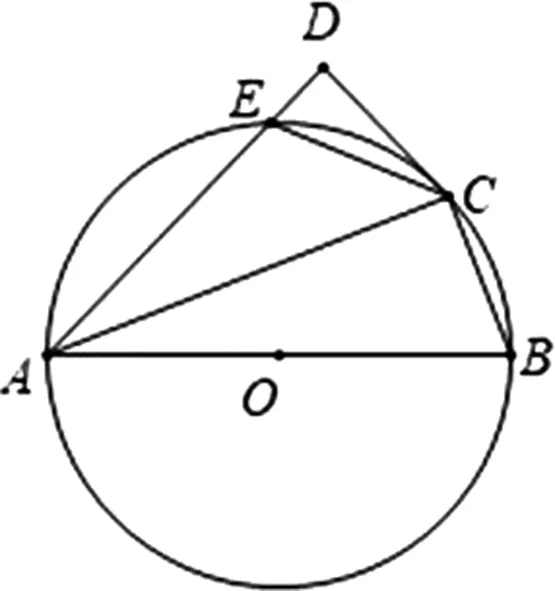
图2

例题.(2019深圳龙岗区二模)如图1，⊙O是△ABC的外接圆，AB是直径，D是⊙O外一点且满足∠DCA=∠B，连接AD.(1)求证：CD是⊙O的切线；(2)若AD⊥CD，CD=2，AD=4，求直径AB的长；(3)如图2，如果∠DAB=45°，且线段AD与⊙O交于E点，问：线段AC、EC、BC之间存在什么数量关系？并说明理由.

解：(1)(2)略

1.截长补短法分析与解题

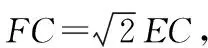
∵AB是直径，∠DAB=45°，∴∠AEB=90°，∴△AEB是等腰直角三角形，∴AE=BE。

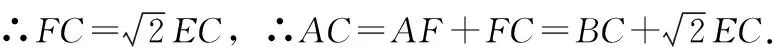
2.托勒密定理巧破截长补短法

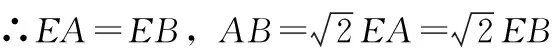
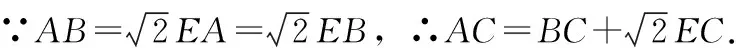
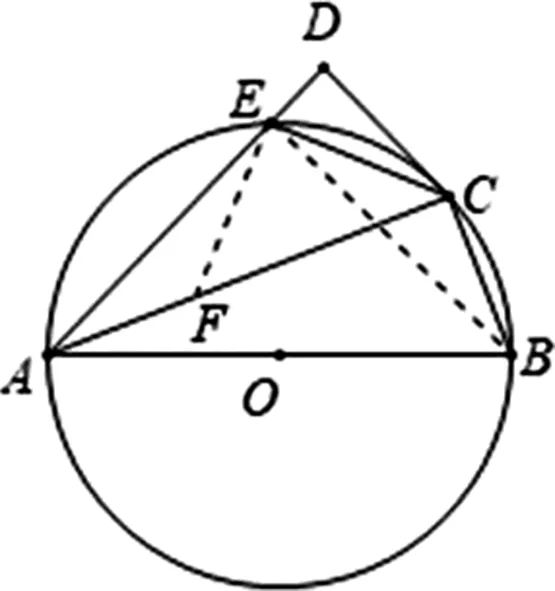
图3

通过以上示例，与传统的截长补短法相比，您可以发现使用托勒密定理处理圆内接四边形的线段之间的数量关系时，托勒密定理更胜一筹.因为无论是截长还是补短，都需要添加至少一条辅助线；而辅助线的问题本身就是初中阶段几何学习的一个难点，成为学生解决此类问题的拦路虎.当几次尝试作辅助线都不能把思路打开时，可以使用托勒密定理，化解“截长补短”的辅助线障碍，带领我们越过“山重水复”而跨入“柳暗花明”的境地，到达事半功倍的效果.