一类定点问题的递进式探究

文/中山市实验中学 王美华

中山市2020学年第一学期期末考试中，高二数学的最后一题在解答时引起笔者很多的思考。监考结束后，笔者借助网络画板的轨迹跟踪功能，就原题结论进行变形，大胆猜想，小心求证，得到一系列结论。下面论述探究和证明的过程。

原题：已知圆O的方程为x2+y2=4，若抛物线C过点A(-1,0),B(1,0)，且以圆O的切线为准线，F为抛物线的焦点，点F的轨迹为曲线R.

(1)求曲线R的方程；

(2)过点B作直线L交曲线R于P、Q两点，P、T关于x轴对称，请问：直线TQ是否过x轴上的定点？如果是，请求出定点的坐标；如果不是，请说明理由.

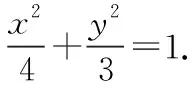
探究1.直线TQ是否过x轴上的定点

发现过定点，下面作理论详细求证，并求出定点坐标.

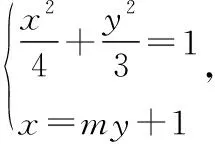
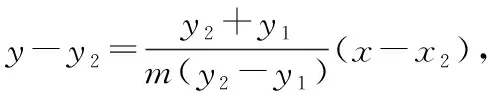
故直线TQ过x轴上的定点(4,0).

探究2.将B换作x轴上任意一点，直线TQ是否依然过x轴上的定点

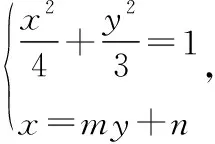
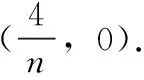
探究3.将B换作x轴上任意一点，将定椭圆方程换成焦点在x轴上任意椭圆，直线TQ是否依然过x轴上的定点

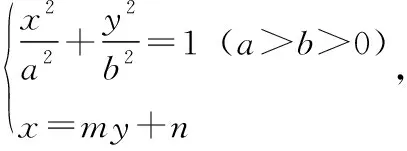
至此，我们可以得到一般性的结论：

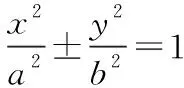
2.直线x=my+n与抛物线y2=2px交于P,Q两点，点P关于x轴的对称点为T，则直线TQ过定点(-n,0)。

圆锥曲线中的定值定点问题很多时候都是通过由特殊到一般的推理过程推得，由椭圆具有的性质推及双曲线和抛物线是否也存在同样的性质。这种归纳推理和类比推理的思维在学习数学中至关重要。