基于极限轨迹的挖掘机工作装置动力学分析*

2020-09-22孙浩然任志贵王军利魏万行

机电工程 2020年9期

孙浩然，任志贵，2，王军利，2，梁杨，魏万行

(1.陕西理工大学机械工程学院，陕西汉中 723000；2.陕西省工业自动化重点实验室，陕西汉中 723000)

0 引言

液压挖掘机作为常用的工程机械，其结构性能受到了国内外众多学者的广泛关注。

在以往的研究中，基于虚拟样机的动力学仿真是众多学者分析挖掘机工作装置的常用方法[1-3]。曹永利[4]基于RecurDyn对工作装置铰点的受力情况进行了理论分析和仿真验证。冯豪[5]基于整体动态模型与局部子模型相结合的方法对工作装置的局部焊缝进行了应力计算。靳龙[6]将柔性联接方式代替了行走架联接螺栓组，得到了几种典型工况下受载最大的螺栓位置及受力曲线。黄鸣辉[7]对工作装置刚柔耦合产生的非线性动力学效应、转动角速度变化产生的惯性以及复合挖掘载荷的不确定性等动态特性进行了仿真分析及实测验证。

综上所述，学者们在考虑挖掘机的载荷时，只考虑了将某一工况下恒定数值的挖掘阻力作为工作装置的静载荷，而未考虑某条挖掘轨迹中随时间改变的动载荷，也未考虑动载荷所对应的工作装置的动态特性。

因此，本文将不同极限挖掘轨迹中液压缸的理论挖掘力作为动载荷，对工作装置铰点力进行动力学仿真分析。

1 极限轨迹选择

液压挖掘机作业范围是由各液压缸行程决定的，液压缸的规律性伸缩使挖掘机完成各个复杂的挖掘动作，使用工作装置的结构参数计算可得挖掘机的包络图[8]。挖掘机包络图是挖掘机性能参数的几何表示，也可看作是挖掘机极限挖掘轨迹的集合。

极限挖掘轨迹中涉及到众多典型的极限工况，如最大挖掘深度工况，并且挖掘机在极限工况下进行挖掘工作对挖掘机工作装置的性能要求较高，挖掘过程中关键铰点的受力比较复杂，所以极限挖掘轨迹是挖掘机工作装置动态特性的研究中极其重要的一环。

挖掘机工作装置各构件之间存在夹角，不同的夹角可使挖掘机工作装置处于不同的工作位置，改变夹角可得到不同的挖掘轨迹。

工作装置夹角范围如表1所示(其中最大角度和最小角度即为挖掘机工作装置的极限夹角)。

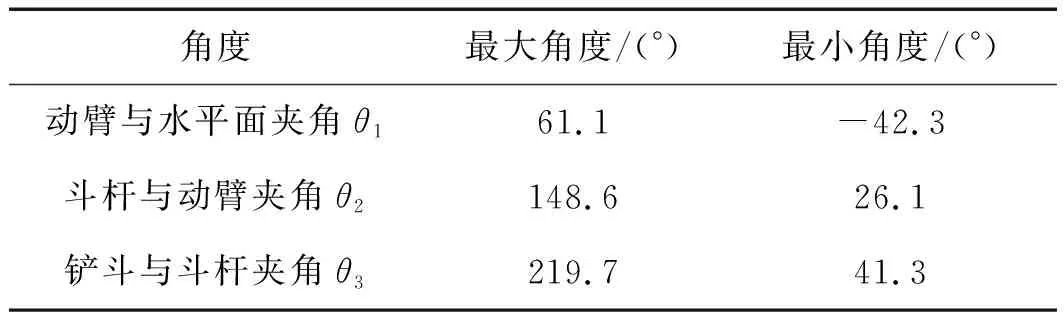
表1 工作装置极限角度

在选择挖掘轨迹过程中，动臂与车身、动臂与斗杆、斗杆与铲斗夹角的初始角与终止角可根据实际需要取值。在此，笔者选择了两条通过最大挖深点D2的极限挖掘轨迹作为研究前提。通过改变斗杆与动臂的夹角θ2，其余夹角保持不变，则可以生成斗杆液压缸极限挖掘轨迹；改变铲斗与斗杆的夹角θ3，其余夹角保持不变，则可以生成铲斗液压缸极限挖掘轨迹。

本研究选择的两条极限挖掘轨迹如图1所示。

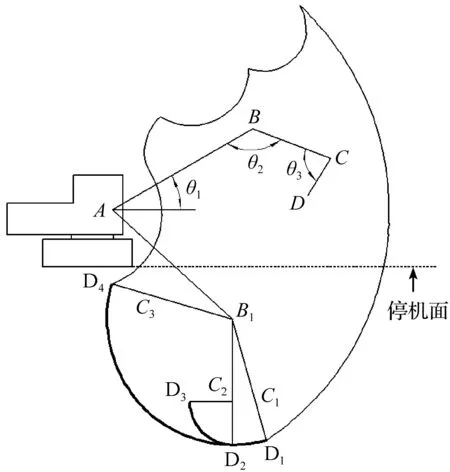
图1 选择的挖掘轨迹

图1中，选择的斗杆液压缸挖掘轨迹为D1至D4，该挖掘轨迹经过挖掘机的最大挖深点D2。此时，动臂与水平面的夹角保持-42.3°，铲斗与斗杆的夹角为180°保持不变，斗杆液压缸伸出，使斗杆与动臂的夹角从148.6°变为26.1°，即完成了极限工作点D1至极限工作点D4运动过程；

选择的铲斗液压缸挖掘轨迹为D2至D3，D2为挖掘机的最大挖深点，此时，动臂与水平面的夹角保持-42.3°，斗杆与动臂的夹角为137.7°保持不变，铲斗液压缸伸出，改变铲斗与斗杆的夹角，使其从180°变为90°，即完成了挖掘机从最大挖深点D2至工作点D3的运动过程。

2 动载荷计算

挖掘力和挖掘阻力是一对相互作用力，液压挖掘机在实际挖掘过程中铲斗所受最大挖掘阻力，即挖掘机在实际工作过程中能发挥出的最大挖掘力。计算出了挖掘机能发挥出的最大挖掘力，也就求出了最大挖掘阻力，即挖掘机的动载荷。

当选定斗杆、铲斗液压缸挖掘轨迹以后[9]，笔者分别在斗杆、铲斗转动角度区间内取等距步长角，即将连续的挖掘轨迹分为等距的挖掘点。

笔者通过理论挖掘力模型，计算出不同夹角对应的挖掘力[10]，最后分别统计出斗杆液压缸挖掘轨迹和铲斗液压缸挖掘轨迹上的理论挖掘力，即铲斗齿尖所受的动载荷，并绘出选定的挖掘轨迹的理论挖掘力图。

液压缸理论挖掘力如图2所示。

斗杆、铲斗液压缸的理论挖掘力随夹角的变化情况分别如图2(a,b)所示。

由图2中可以得到，在挖掘过程中，斗杆、铲斗液压缸的挖掘力随角度的减小呈现先缓慢增大后急剧减小的情况；其中，斗杆液压缸在夹角θ2为86°时最大，最大挖掘力为88.391 kN；铲斗液压缸在夹角θ3为131°时最大，最大挖掘力为104.289 kN。

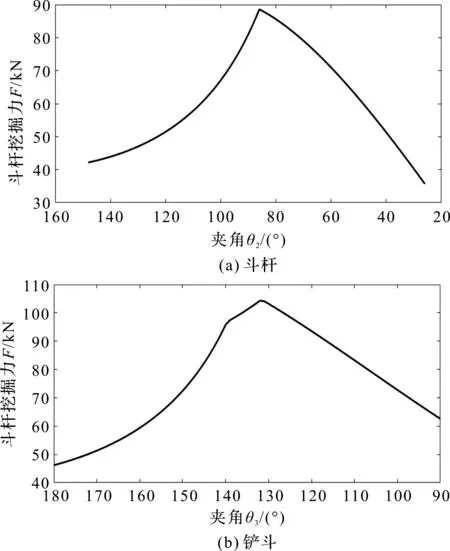
图2 液压缸理论挖掘力

3 动态特性仿真分析

3.1 动力学模型

为了减少动力学仿真时间且不影响仿真结果，在建模过程中，笔者对工作装置进行简化处理。

工作装置实体模型如图3所示。

图3 工作装置实体模型

导入后的模型需要在marker点上对各构件建立相应约束，工作装置约束副如表2所示。

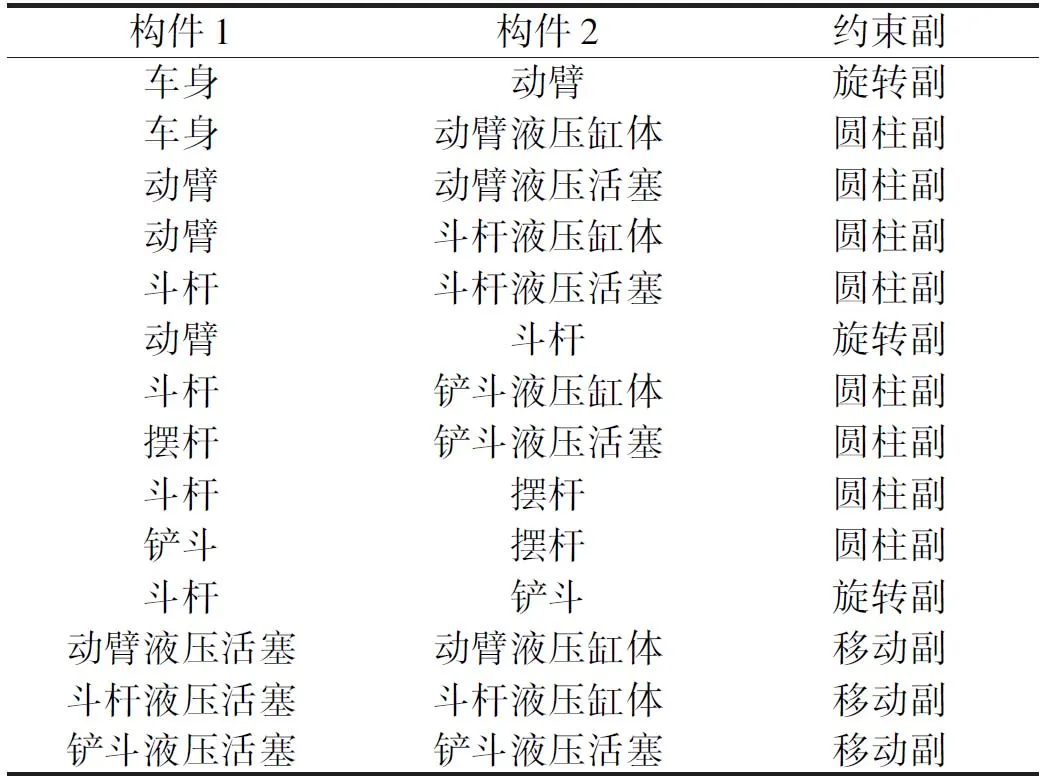
表2 工作装置约束

实际工作过程中，在忽略土壤摩擦力对工作装置运动影响的情况下，液压挖掘机工作装置所承受的外来负载主要包括挖掘阻力和斗中物料重力。笔者将第2节中计算得到的理论挖掘力看作铲斗所受的动载荷，其由切向力和法向力两部分组成，分别用Ft和Fn表示，并且根据经验定义法向挖掘力是切向挖掘力的0.2倍，即Fn=0.2Ft，方向分别为沿挖掘轨迹的切线和法线方向。

物料重力计算公式为：

G=ρ·v·g

(1)

笔者取挖掘土壤的疏松程度为Ⅲ级，挖掘的土方量为标准斗容v=0.9 m3，Ⅲ级土壤的密度为ρ=1.8×103kg/m3，则铲斗装满物料时重力G=15 876 N。

进行仿真时，笔者通过STEP函数来控制液压油缸的伸缩行程与动载荷的加载，在铲斗齿尖建立作为测量的maker点。

工作装置STEP函数如表3所示。

表3 工作装置驱动函数表

3.2 模型验证

本研究使用Matlab软件，结合工作装置结构参数对最大挖深点进行理论计算。挖掘机工作装置包络图如图4所示。

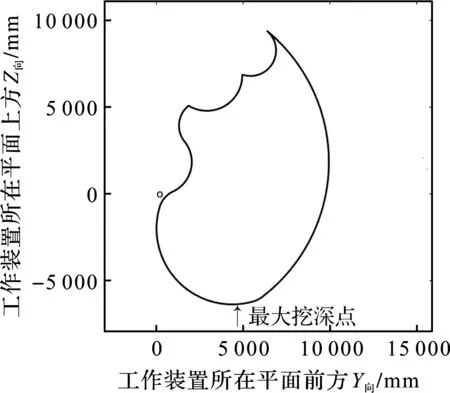
图4 挖掘机工作装置包络图

由图4可知，挖掘机工作装置最大挖深点在YZ平面内的坐标为(4 500，-6 300)，单位为毫米。在仿真软件中对液压挖掘机模型进行运动学仿真。

仿真时间设置为50 s，仿真步长为200，可得到各关键零件和铰点的位移和受力变化情况。

铲斗斗齿齿尖的位移曲线如图5所示。

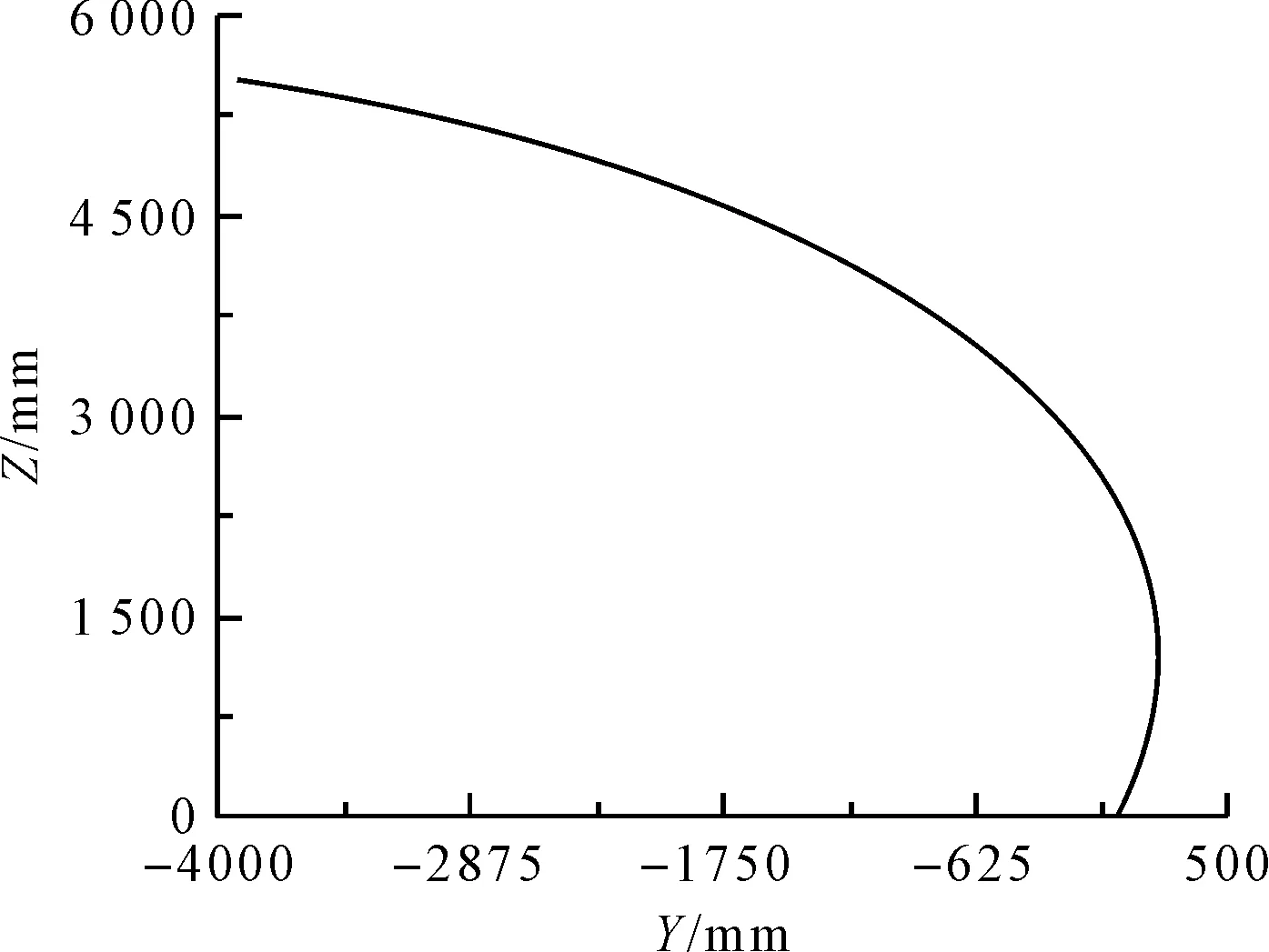
图5 斗杆挖掘齿尖位移

由图5可以看出:在斗杆液压缸挖掘过程中，工作装置在YZ平面内的最大挖深点坐标为(4 200，-5 700)，通过与理论计算得到的斗齿尖位移进行对比，Y、Z方向上误差分别为6.67%、9.52%。

虽然位移存在一定误差，但仍旧在允许的范围内，因此，仍可认为所建立的动力学模型是合理且有效的。

3.3 仿真结果分析

工作装置铰点受力情况如图6所示。

图6 铰点受力JOINT2—动臂与车身铰接点；JOINT5—斗杆与动臂铰接点；JOINT12—铲斗与斗杆铰接点

图6(a)中，在使用斗杆液压缸进行挖掘过程中，即斗杆液压缸挖掘轨迹为D1至D4，动臂与车身铰点JOINT2的受力在t=0～12 s内由62.5 kN急剧减小至0 kN；铰点力由Y轴负方向变为正方向，在t=12 s～33 s内急剧增长达到最大峰值，峰值铰点力为100 kN，在t=33 s～50 s内缓慢减小至56.25 kN；

斗杆与动臂铰点JOINT5的受力在t=0～35 s内缓慢增长，并在35 s时达到最大峰值，峰值铰点力为140 kN；在t=35 s～47 s内急剧减小，47 s时减小至0 kN，同时铰点力由Y轴正方向变为负方向；

仿真过程中，铲斗与斗杆铰点JOINT12的受力方向一直为Y轴负方向，在t=0～39 s内先增后减直至变为0 kN，t=22 s时达到最大峰值，峰值铰点力为53.125 kN，在t=39 s～50 s内缓慢增长。在挖掘过程中，斗杆与动臂铰点JOINT5的受力最大，最大铰点力约为140 kN。

图6(b)中，在使用铲斗液压缸进行挖掘过程中，即铲斗液压缸挖掘轨迹为D2至D3，动臂与车身铰点JOINT2的力在t=0～13 s内由62.5 kN缓慢减小至0 kN，在t=13 s时急剧增长，同时，铰点力由Y轴负方向变为正方向，40 s～50 s时铰点力趋于稳定，并在45 s时达到最大峰值，峰值铰点力为162.5 kN。

斗杆与动臂铰点JOINT5的受力由t=0 s开始缓慢增加，t=40 s趋于稳定，并在45 s时达到最大峰值，峰值铰点力为170 kN。铲斗与斗杆铰点JOINT12的受力在0～35 s内先增后减，t=35 s时开始急剧增长；同时，铰点力由Y轴负方向变为正方向，并在50 s时达到最大峰值，峰值铰点力为102.5 kN。在挖掘过程中，斗杆与动臂铰点JOINT5的受力最大，最大约束力约为170 kN。

从图6可见：

(1)在斗杆、铲斗两种挖掘轨迹仿真过程中，动臂与车身铰接点JOINT2、斗杆与动臂铰接点JOINT5的受力变化趋势基本一致，而铲斗与斗杆铰接点JOINT12受力变化比较明显。并且，斗杆与动臂铰接点JOINT5受力变化最平稳，且峰值最大；铲斗与斗杆铰接点JOINT12受力变化最剧烈，且峰值最小；

(2)液压挖掘机动臂、斗杆上的各铰点的受力情况随动载荷的变化而变化，最大值与理论挖掘力的峰值出现时间基本一致。