变载荷铣削力影响下的加工中心床身结构优化设计*
2020-09-22梁丽强萨日娜
梁丽强,萨日娜,2,3*,高 峰
(1.内蒙古工业大学 机械工程学院,内蒙古 呼和浩特 010051;2.浙江大学 机械工程学院,浙江 杭州 310027;3.康力电梯股份有限公司,江苏 苏州 215213)
0 引 言
加工中心在现代化工业中有着广泛的应用,床身结构作为机床重要的基础支撑件对机床的布局有很大的影响。床身的结构尺寸和布局形式,直接影响机床的加工精度、精度稳定性和生产效率。床身设计不合理,刚度不足,会引起床身的各种变形和振动[1]。
目前,提高机床加工性能的常用方法有优化机床的结构和应用新型材料制造机床两种[2-3]。MA Y L[4]在加工中心床身的结构优化中使用了拓扑优化的方案,完成了床身结构优化,使得床身刚度和动态性能都得到相应提高;SIGMUND O[5]针对宏观结构、微观结构的制造,提出了一种基于拓扑优化的延伸方法;赵二新等[6]在车削中心床鞍轻量化设计中使用了拓扑优化,实现了结构轻量化设计;崔争争[7]提出了针对多个目标采用加权平均的方法,把多目标优化问题转化为单目标优化问题;张昆鹏[8]针对拓扑优化模型求解过程中,需要多次迭代才能得到满足一定精度要求的收敛结果的问题,提出了一种基于向量Epsilon算法加速迭代序列收敛的方法;陈垂福[9]基于固体各向同性材料理论,对悬臂梁进行了拓扑优化设计,建立了悬臂梁拓扑优化数学模型,求解了位移约束下悬臂梁体积最小的拓扑结构;TENERELLI P等[10]提出了一种基于GIS的多标准、多目标和不确定性分析的方法,来评估能源作物转换的一系列可能性;饶柳生等[11]把柔度最小和1阶固有频率最大作为目标进行了多目标优化,结合拓扑优化方法对立柱的筋板结构进行了改进;姜衡[12]在加工中心多目标优化中采用响应面法,实现了加工中心的结构优化,使其静动态特性均得到了较好的提升;马雅丽[13]在不确定因素影响下的机床支撑件多目标稳健性设计中,通过灵敏度法和支持向量机方法,实现了机床支撑件的结构优化设计。
对于铣削加工时,考虑铣削加工过程中铣削力随时间变化的变载荷对床身结构优化的影响;同时当模型外形较复杂结构尺寸较大时,都对有限元优化求解的效率产生了不利的影响。所以本文针对加工中心床身的结构优化过程合理地定义了拓扑优化的变载荷施加;在多目标尺寸优化过程中将床身拆解成小的单元结构来完成床身的尺寸优化,既可以减少计算的求解时间,又能有效地完成模型的优化设计。
针对以上问题,本文对床身进行多目标优化,使床身结构更加合理有效。
1 加工中心床身结构拓扑优化
1.1 加工过程中变载荷切削力及工况分析
笔者主要对加工中心铣削加工时动态铣削力对床身结构优化的影响加以研究。
以加工中心进行铣削加工为例,铣刀为圆柱形铣刀,根据铣削公式[14],有:
(1)
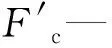
(2)
式中:Ff—纵向进给力;Fe—横向进给力;Ffn—垂直进给力。
计算得到Ff=1 000 N,Ffn=1 100 N,Fe=1 400 N。切削是一种周期性切削过程,其周期为刀具旋转一周的耗时[16]。
以周期为0.15 s,铣削力随时间周期变化的规律及铣削力的传递路径,如图1所示。

图1 变载荷铣削力分力及其传递路径
加工中心铣削加工时,按照工作台的不同位置来划分加工中心的不同工况,如图2所示。
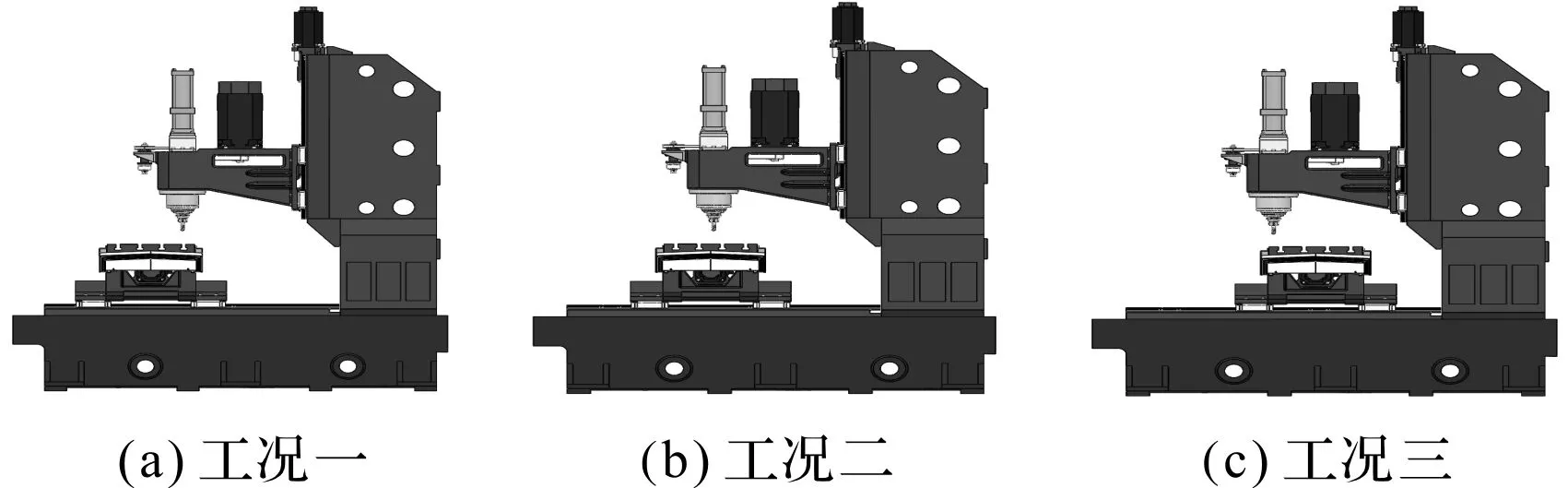
图2 加工中心工况分析
图2中,工况一:工作台位于导轨的左端的极限位置;工况二:工作台位于导轨中间位置;工况三:工作台位于导轨右侧极限位置。
1.2 加工中心床身变载荷拓扑优化数学模型
鉴于SIMP算法具有较好的收敛性和应用价值,笔者选择SIMP模型变密度法,对机床底座进行优化设计[17-18]。
在结构优化中,通常将刚度目标函数转化为柔度目标函数进行求解,柔度可以通过结构的应变能来表示:
(3)
式中:Ci—第i个工况下,床身结构柔度;Fi—第i个工况下,有限单元节点载荷向量;Ui—第i个工况下,有限单元节点位移向量;Vi(x)—拓扑优化后,床身结构体积;V0—原始体积;f—体积分数约束取值为0~1。
因此,通过折衷规划法得到结构柔度最小[19]的目标函数为:

(4)
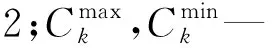
以低阶固有频率最大为目标的拓扑优化中,会遇到当某一阶固有频率达到最大值时,而其他阶固有频率下降到了很小的值,优化结果难以满足设计要求[20]。因此,在低阶固有频率的优化时,需要综合考虑多阶频率,即:
(5)
式中:Λ(x)—频率的平均数;z0,k—调整目标函数的参数;f—所优化的频率阶数;ωi—频率权值;λi—第i阶特征频率。
同时,考虑结构柔度和固有频率的多目标拓扑优化目标函数,变量xi来表示i单元相对密度ρi,可得到多目标拓扑优化的综合目标函数:

(6)
式中:xi—优化设计变量,代表离散材料单元i的相对密度,取值为[xmin,1]之间的连续值;ω—柔度目标函数的权值;1-ω—固有频率目标函数的权值;Λmax,Λmin—平均频率的最大值、最小值;Vi—拓扑优化结果的结构体积;V0—结构优化前体积;fv0—拓扑优化允许的体积上限值。
为了有效避免总刚度矩阵出现的奇异现象,取Xmin=0.001。
1.3 加工中心床身的拓扑优化设计
1.3.1 加工中心床身有限元模型的建立
床身的三维模型和有限元模型如图3所示。
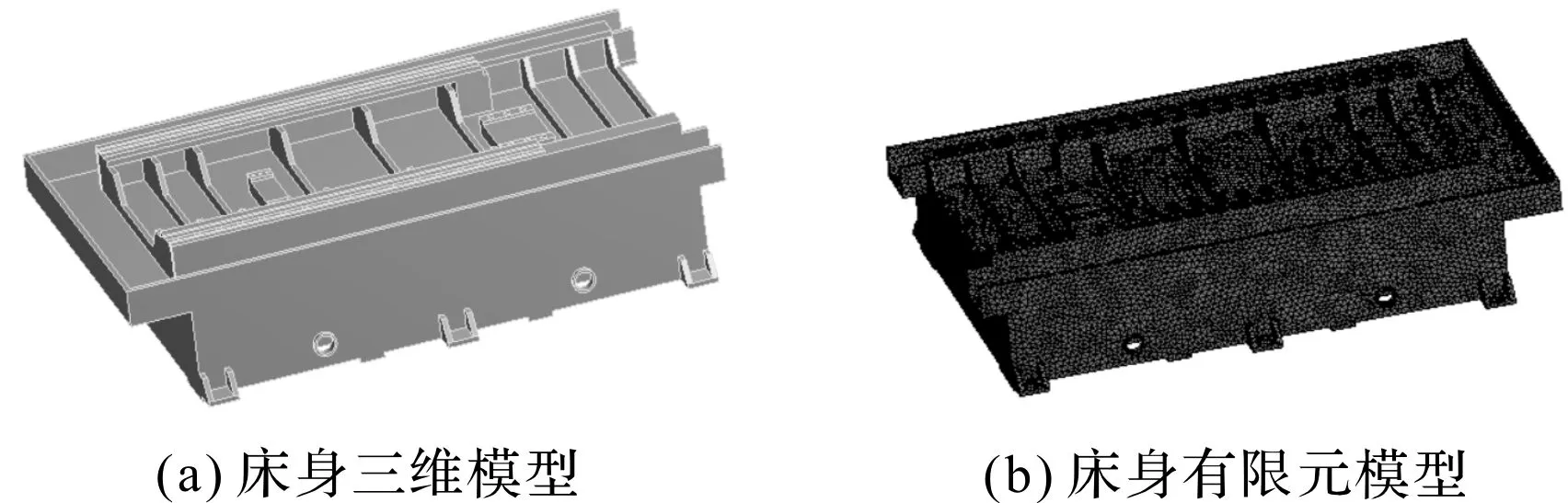
图3 床身模型
图3中,床身的材料为HT200,弹性模量为148 GPa,泊松比为0.26,密度为7 200 kg/m3,床身质量为993.7 kg;床身长1 968 mm,宽1 290 mm,高456 mm,壁厚16 mm;床身内部设计有不同位置的加强筋厚度为16 mm,筋板与外壁均设计有出砂孔。
采用Workbench网格划分技术,对加工中心床身模型进行网格划分,共得到312 611节点和164 870个单元。
1.3.2 加工中心床身的载荷与约束条件
床身主要受两部分力的作用,一部分是铣削力的作用,另一部分是安装在床身上的立柱、刀库、主轴组件、工作台等部件的压力。
将铣削力按照周期为0.15 s,加载到加工中心床身上。将铣削力沿着加工中心工作台的运动方向进行分解,纵向进给力垂直作用于导轨侧面,其值为2 200 N,垂直进给力方向为垂直于两导轨,其值为2 800 N,以及滑座和加工工件总质量420 kg,横向进给力沿导轨方向其值为2 000 N,以及床身上的立柱、刀库、主轴组件、工作台总质量施加给床身的力。
床身的载荷和约束如图4所示。

图4 床身载荷与约束
床身是由底部的6个螺栓与地面固定,所以笔者对6个螺栓孔施加完全约束。横向进给力施加于床身导轨沿X轴正方向,纵向进给力作用在导轨侧面沿Y轴正方向,垂直进给力施加于垂直导轨沿Z轴正方向,以及床身上的立柱、刀库、主轴组件、工作台总质量施加给床身的力沿Z轴正方向。
笔者基于Workbench中Topology Optimization模块,对床身有限元模型进行拓扑优化[21-22]。
在Workbench中,笔者对加工中心床身模型进行约束设置,体积分数设置为0.7~0.8,定义设计区域与非设计区域。优化以提高动态特性为主,故选取综合目标函数式中固有频率项的权值为0.6,柔度项权值为0.4。
拓扑优化目标及权重设定如表1所示。

表1 拓扑优化目标及权重设定
在保证床身前三阶固有频率和柔度的情况下,得到结构的最佳材料分布。
在Topology Opitimization求解器中,对设计空间进行分析。
设计空间稳定之后,床身得出的拓扑形态以及拓扑优化目标函数的迭代过程,如图5所示。


图5 拓扑优化形态及其迭代过程(a)—拓扑优化收敛稳定后的拓扑形态;(b)—前三阶固有频率迭代过程;(c)—拓扑优化过程中床身体积迭代过程;(d)—多目标拓扑优化综合函数经过45次迭代收敛过程;(e)—根据床身结构拓扑优化结果,建立了新的床身方案模型
1.3.3 加工中心床身新方案性能评估
新的床身方案模型按照拓扑优化模型指导的去除率进行建模,去除了多余的筋板并且在床身的前后位置以及侧面进行开孔设计。
将床身的新旧模型进行分析对比,其性能参数对比如表2所示。

表2 优化前后床身性能参数对比
2 床身结构单元多目标尺寸优化
响应面分析作为尺寸优化的一种有效方法,其可以在继承多目标拓扑优化的基础上,进一步完成加工中心尺寸优化。
将床身整体结构拆分成小基本单元结构,进行响应面分析,既可以减少计算的求解时间,又能有效地完成模型的优化设计。
基本单元结构如图6所示。
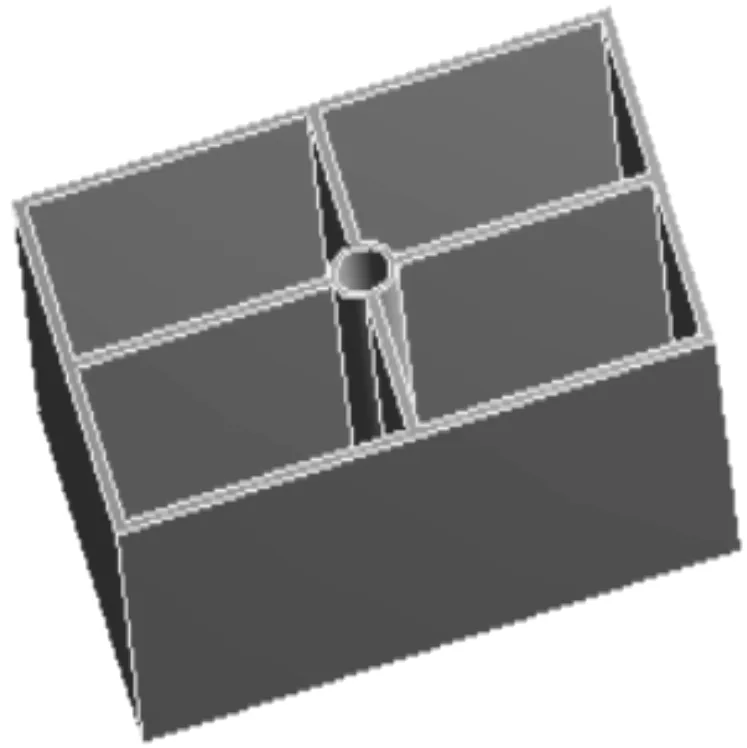
图6 基本单元结构结构
笔者定义了5个设计变量和两个目标函数,分别为P1单元壁厚、P2单元拉伸高度、P3单元筋板厚度、P4单元长度、P5单元宽度。目标函数为P6单元固有频率、P7单元质量。
为了构建标准二阶响应面模型,笔者首先对定义的5个设计变量进行灵敏度分析[23],如图7所示。
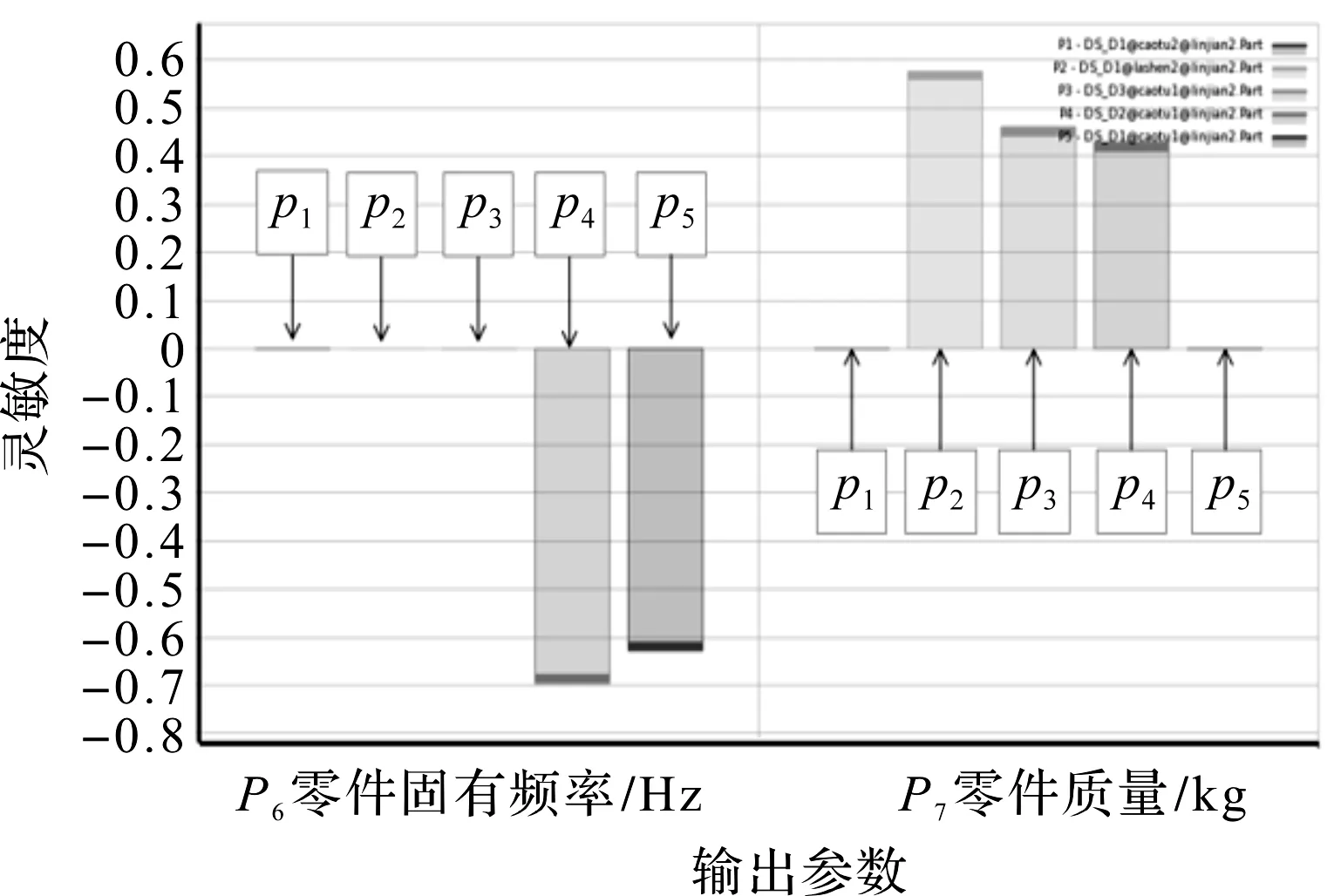
图7 灵敏度分析图
由灵敏度分析图可以看出,P1设计变量对单元的两个目标函数影响较小,予以剔除。故将其与4个设计变量作为构造响应面优化的设计变量。
然后采用Optimal Space-Filling Design最佳填充空间设计方法,在样本空间生成25个样本点,如表3所示。
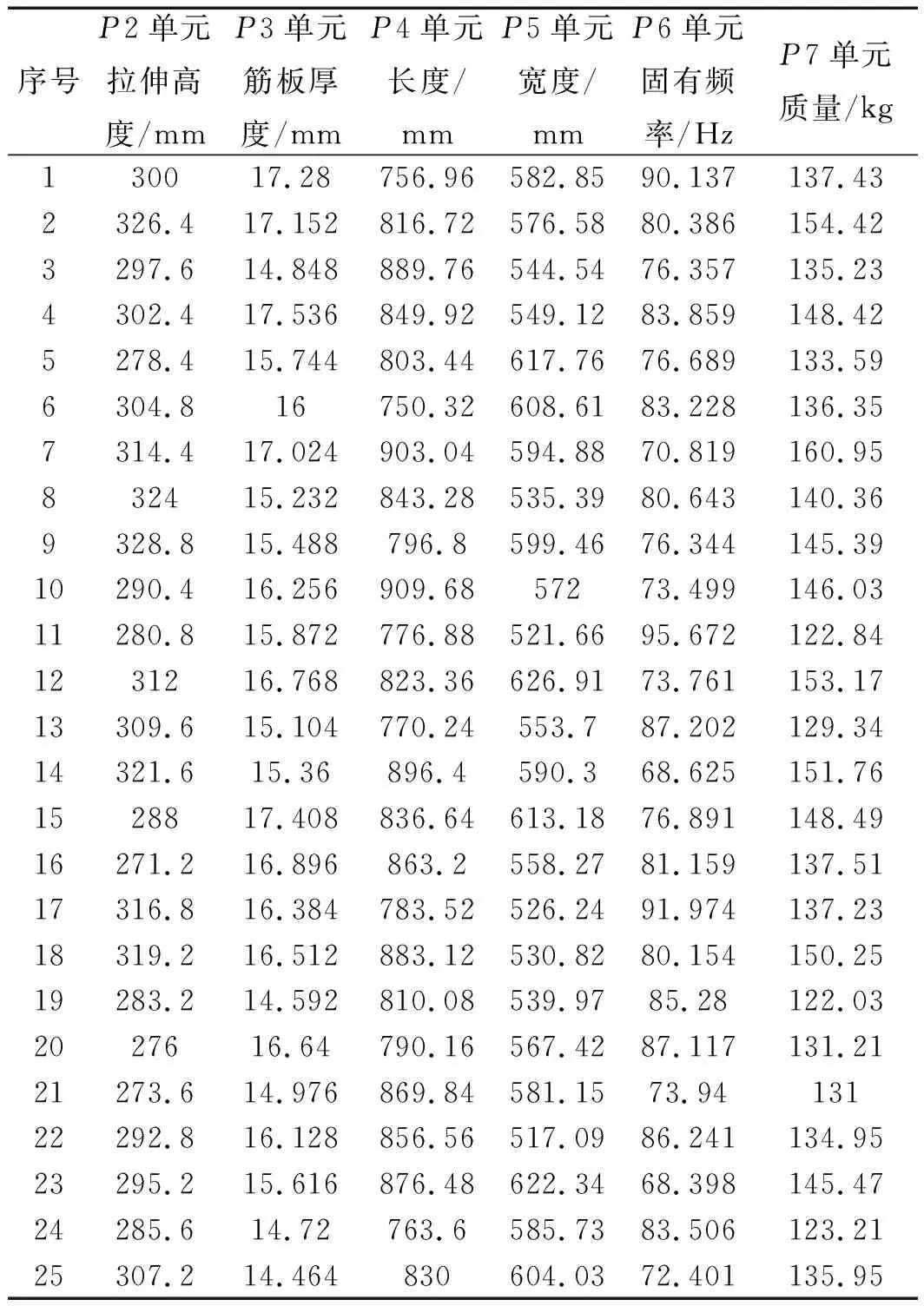
表3 抽样所生成的空间样本点
通过Workbench更新计算,得到样本点对应的响应值。
将样本数据导入response surface中,进行响应面模型的构建,如图8所示。

图8 结构单元响应面模型
响应面优化结果的有效与否受其拟合精度影响,故对响应面的拟合精度进行评估,如表4所示。

表4 响应面拟合精度
表4中,给出了响应面模型拟合精度;其中,P6和P7分别表示单元一阶模态频率总质量和一阶模态频率。可知该响应面模型精度满足要求,可用于后续的多目标优化求解。
在Workbench中,基于床身质量和一阶固有频率建立的响应面模型,采用MOGA优化算法进行优化求解,其优化算法求解参数设置如表5所示。

表5 MOGA优化参数设置
最终优化得到的3组候选点如表6所示。
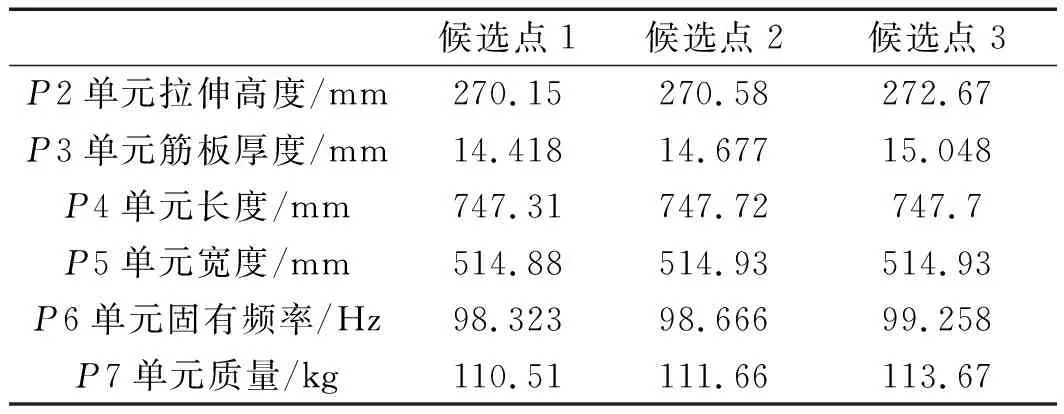
表6 优化后的候选点
3组候选点的拟合精度都符合实验设计精度要求,因此,将第3组候选点作为最终优化方案。
将第3组候选点方案与原模型进行比较,如表7所示。
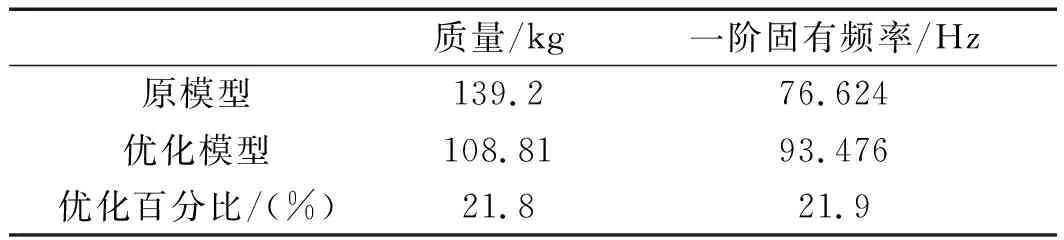
表7 优化方案与原模型性能参数对比
由表7中可以看出:结构单元的一阶固有频率优化了21.9%,质量减少了21.8%。
3 优化结果性能分析及对比验证
3.1 优化结果性能分析
将响应面优化后的单元结构尺寸代入床身模型中,对比优化后床身模型与原模型以及拓扑优化模型,如表8所示。
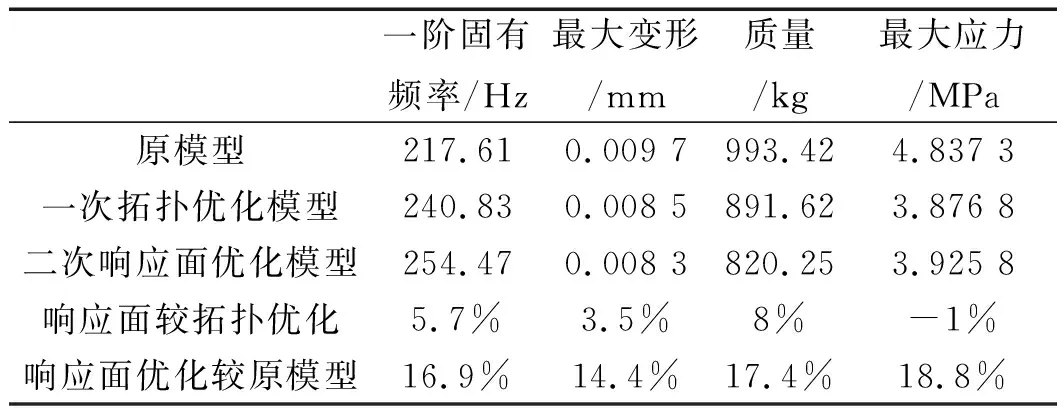
表8 优化后结构性能参数对比
3.2 对比验证
基于Ansys有限元分析软件,笔者实现了加工中心床身的多目标拓扑优化以及结构尺寸优化。
为验证结果的有效性,故将优化结果与Hyper Works有限元分析结果进行对比,如图9所示。

图9 对比验证
从图9中可以看出:其拓扑优化后的材料保留基本一致;比较其相关结构性能参数可知,采用本文方案得到的最终优化结果较hyperworks优化结果在结构性能方面都有不同程度的提高,证明了本文采用的优化方案是合理有效的。
4 结束语
本文针对加工中心工作过程中变载荷铣削力对床身结构性能的影响问题,提出了以床身固有频率和柔度为目标,体积分数为约束条件的多目标拓扑优化设计方法;从床身整体方面,采用折中规划法和平均频率法,构建了变载荷铣削力影响下的多目标拓扑优化的数学模型;依据变密度法拓扑优化,获得了加工中心床身的最佳结构布局;在此基础上,从床身结构单元方面借助经过优化的拉丁超立方采样,构造了单元标准二阶响应面,使用多目标遗传算法对床身进行多目标尺寸优化。
优化结果表明:床身固有频率增加16.9%,床身质量减少17.4%,最大变形量降低14.4%,最大应力降低18.8%。
该优化方案使加工中心床身的结构布局更加合理,实现了轻量化设计,有效地提高了床身的各项力学性能,并且有较高的设计效率。
对于床身的多目标结构优化时,关于目标函数权重的选取具有一定的经验成分,笔者的下一步工作将针对多目标函数的不同权重系数,对结构优化产生的影响进行研究。
