无线通信中的信噪比估计算法研究

刘剑锋，李瑞华 ，刘垚圻，4，苏泳涛，胡金龙

1.国家移动卫星通信工程技术研究中心，南京 210002

2.中国科学院 计算技术研究所 无线通信技术研究中心，北京 100190

3.中国科学院大学 计算机科学与技术学院，北京 100049

4.中国科学院 计算技术研究所 南京移动通信与计算融合创新研究院，南京 211135

1 引言

无线通信技术应用广泛。信噪比估计作为无线通信中的一个环节，其意义重大：信道均衡、功率控制、调制识别、Turbo 迭代译码等很多场合都需要信噪比作为先验知识；自适应系统中的自适应编码调制、自适应多波束分配、自适应越区切换、自适应载波恢复等众多技术，也都需要精确的信噪比估计值以保证自适应系统能够在各种复杂环境下正常运行[1-3]。

信噪比估计算法已被大量研究。各种信噪比估计算法，所需条件不同，适用场景不同，性能和表现也各有特点。本文第2 章对文献中经典的信噪比估计算法进行总结，讨论了各种经典算法所需的先验知识以及适用条件，以减小实际应用中不同环境下信噪比估计方案的设计难度。

大部分文献在对信噪比估计算法进行研究时，普遍考虑数据长度和频偏对算法性能的影响，却很少考虑滤波器和上下采样的影响。另外，绝大多数文献在对信噪比估计算法进行仿真的时候，仿真系统中并未考虑上下采样。本文欲在含有滤波器和上下采样的仿真系统上对第2 章中的经典信噪比估计算法进行性能仿真。在进行仿真之前，需要做一些关于滤波器和上下采样的研究：本文第3章从发送端的上采样和脉冲成型滤波器以及接收端的匹配滤波器和下采样的角度出发，首先搭建仿真系统，研究滤波器和上下采样对信噪比的影响，然后在此基础上研究滤波器和上下采样对信噪比估计算法性能的影响。另外，研究滤波器和上下采样的影响，可以在实际中选择滤波器滚降系数、上下采样倍数、信噪比估计算法时能综合考量前两者对第三者的影响。

本文第4 章利用前面搭建的带有滤波器和上下采样的仿真系统，对文献中经典的信噪比估计算法进行仿真，以得到在考虑上下采样的情况下性能较优的算法。

2 已有信噪比估计算法

不同文献对信噪比估计算法进行研究的时候，由于系统和需求的不同，对接收机接收到的信号作的模型假设不同。综合各种文献来看，一种常见且通用的信号模型[4-5]如式（1）所示：

y(n)表示接收到的信号；s(n)表示真正有用的已调信号；w(n)表示广义信道中的加性高斯白噪声；h(n)则表示信号在经过信道过程中幅值和相位上的变化，引起这种变化的原因包括发送端的脉冲成型滤波器、时延、频移、相偏、信道损耗等。

根据是否必须使用辅助数据，可以将文献中经典的信噪比估计算法分为两类：一类是必须使用辅助数据（诸如导频等接收端已知其信号值的训练序列）的信噪比估计算法（DA）；一类是不需要必须使用辅助数据，即不需要已知信号值的信噪比估计算法（NDA）。DA 在一定程度上会增加整个通信系统的开销，从而降低吞吐量；NDA 则需要使用足够长的观测数据以保证估计结果的稳定性。

文献中的数据辅助类算法主要有：基于子空间分解的算法（SD）[6-8]、最小二乘算法（LSE）[9]、最大似然估计算法（ML）[9]。非数据辅助类算法主要有：二阶-四阶矩估计算法（M2M4）[10]、高阶累积量估计算法（CUM）[11]、二阶-四阶-六阶矩算法（M2M4M6）[12]、M2M4_QAM 算法[12]、分割符号矩的估计算法（SSME）及其改进算法（改进的SSME）[2，13]、广义的分割符号矩的估计算法（GSSME）[13]、数据拟合算法（DF）[12，14]、基于样本特征函数的信噪比估计算法（ECF）[12]、信号方差比估计算法（SVR）[15]、JLG算法、功率算法（power）及优化的功率算法（优化的power）。这些信噪比估计算法需要的先验知识各不相同，一般来说其需要的先验知识主要包括辅助数据、调制方式等。综合各种文献，列出各个算法需要的先验知识，如表1所示。

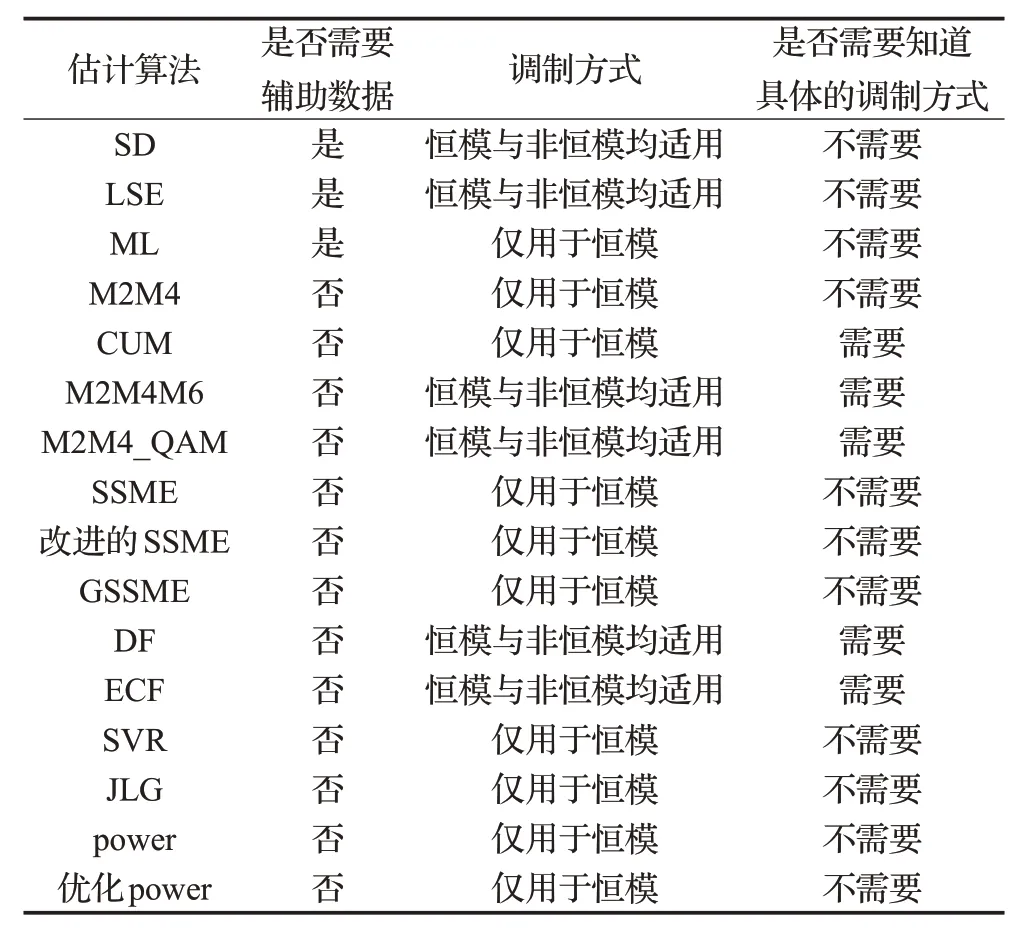
表1 文献中各算法所需先验知识

算法所需先验知识对算法的使用有很大影响，因为在有些情况下可能没有办法知道调制方式等信息。对表1中信噪比估计算法的先验知识进行简单分析，可以知道恒模与非恒模调制方式均适用且不需要知道具体调制方式的算法有SD算法、LSE算法。

SD 算法的基本原理是对训练序列的协方差矩阵（Toeplitz 矩阵）进行奇异值分解，其奇异值经过简单处理就可以得到噪声和信号的功率谱密度函数，从而计算出信噪比估计值；该算法从空间结构的角度入手，信噪比估计性能良好。LSE 算法的基本原理是使接收到的训练序列观测值与原本的训练序列假设值之间的误差平方和最小，以此得到信噪比估计值。ML算法即最大似然估计。M2M4、CUM、M2M4M6 以及M2M4_QAM算法均通过计算接收信号的高阶矩来进行信噪比估计。SSME、改进的SSME、GSSME 算法是通过对每个符号进行过采样计算信噪比的，适用于信息速率比较低的深空通信。对于DF 算法，要预先仿真得到高阶统计量与信噪比之间的关系，之后便可以通过计算接收信号的高阶统计量得到信噪比估计值。ECF 算法利用样本特征函数进行信噪比估计。SVR 算法则实际上是另一种使用高阶矩统计量进行估计的方法。JLG、power、优化power算法均是通过二阶矩计算信噪比的方法。

除了以上经典的信噪比估计算法，文献[16]提出了一种基于修改的sigmoid 增益函数的先验信噪比估计器，克服了DD（决策导向）信噪比估计中的延迟。文献[17]针对线性系统，提出了一种根据接收信号的单一实现进行信噪比估计的高精度算法。文献[18]对衰落信道模型中的信噪比估计技术矩量法进行了研究。文献[19]提出一种基于谐波重构的先验信噪比估计算法，在低信噪比下能有效增强高次谐波分量，提升语音增强算法的性能。文献[20]提出了新的改进DD先验信噪比估计结合基于语音存在概率的噪声估计算法，对噪声功率谱的估计性能较好，噪声急剧变化时仍能实时跟踪。文献[21]针对无人机中的数据链通信，将卷积神经网络（CNN）与长短时记忆网络（LSTM）相结合，来进行信噪比估计；这是较早的将深度学习应用于信噪比估计的算法之一，与以往算法相比，该算法具有较高的估计精度。文献[22]提出了一种对实时长期信噪比进行估计的算法——自适应长期信噪比估计算法（ALTIS）；只有信号或噪声发生非瞬态变化时才能改变算法信噪比估计值；该算法计算成本低，更新速度快，适用于实时语音处理。

由于SSME、改进的SSME、GSSME算法比较特殊，均基于接收系统从模拟到数字部分的过采样，且上述几种较新的估计算法均有特定的应用场景，在一般的无线通信系统中并不通用，本文后面在对文献中的算法进行仿真的时候，为了基带仿真系统的简易性，暂且先不考虑这些算法的仿真。

3 滤波器和上下采样的影响

无线通信系统在进行数字信号处理的时候，一般会有上下采样、成型滤波器、匹配滤波器等模块[23]，而大多数文献在进行信噪比估计时并没有研究滤波器和上下采样对信噪比的影响，也没有考虑滤波器和上下采样对信噪比估计算法的影响。不同的信噪比估计算法对滤波器滚降系数、上下采样倍数等的敏感程度不同，所以滤波器滚降系数和上下采样倍数等将影响着实际应用中信噪比估计算法的选择。本章将搭建一个简易的仿真系统，并基于这个系统，首先研究滤波器和上下采样对真实信噪比的影响，然后研究其对信噪比估计算法性能的影响。

3.1 仿真系统的搭建

本文采用的仿真系统的结构图如图1所示。

为了方便后面的分析，图1描述了A、B、C三个仿真系统。A 系统表示输入已经调制的基带信号，经过信道，使用输出的信号进行信噪比估计；B 系统表示输入已经调制的基带信号，经过脉冲成型滤波器、信道、匹配滤波器，使用输出的信号进行信噪比估计；C 系统表示输入已经调制的基带信号，经过上采样、脉冲成型滤波器、信道、匹配滤波器、下采样，使用输出的信号进行信噪比估计。

上采样采用补零内插。上采样和下采样使用相同的采样倍数，以保证基带调制和基带解调相同的符号速率。脉冲成型滤波器和匹配滤波器均采用平方根升余弦滚降低通滤波器。对于信道，这里暂且不考虑时延、频偏、相移、损耗等的影响，仅仅加入加性高斯白噪声。也就是说，对于式（1）中的信号模型，A系统的h(n)值为1，B 系统的h(n)仅包含滤波器的影响，C 系统的h(n)包含滤波器和上下采样的影响。

3.2 滤波器和上下采样对信噪比的影响

利用前面搭建好的仿真系统，下面开始研究滤波器和上下采样的影响。在3.3节研究滤波器和上下采样对信噪比估计算法的影响之前，首先研究滤波器和上下采样对信噪比的影响。不同于3.3节对算法的估计值进行分析和计算，本节是对信噪比真实值进行分析。

以QPSK调制信号为例，研究滤波器对信噪比的影响。在信道中加入噪声，使A系统输出位置的真实信噪比在[-10 dB,10 dB]范围内变化，比较B系统输出信号的真实信噪比相比于A 系统输出信号的真实信噪比发生了哪些变化。符号速率为10 MHz，蒙特卡洛仿真50次，数据长度为50 000，B系统中的滤波器滚降系数分别为0.25、0.35、0.5时的仿真结果如图2（a）所示。

之后研究上下采样对真实信噪比的影响（上采样与下采样倍数相同）。在信道中加入噪声，使A 系统输出位置的真实信噪比在[-10 dB,10 dB]范围内变化，比较C 系统输出信号的真实信噪比相比于B 系统输出信号的真实信噪比发生了哪些变化。同样是以QPSK 调制为例，符号速率为10 MHz，蒙特卡洛仿真50次，B系统和C系统的滤波器滚降系数均为0.35，数据长度为500 00，C系统中的上下采样倍数分别为5、10、20时的仿真结果如图2（b）所示。

观察图2（a），“A系统真实信噪比值”是未加滤波器情况下的信噪比值，“B系统真实信噪比值”则是加了滤波器之后的信噪比值。从仿真图中可以看出，滤波器使得真实信噪比值变大。将仿真图放大观察，发现加了滤波器之后的真实信噪比值（即B系统输出信号的真实信噪比值）是曲线，即不再随着A 系统输出信号的真实信噪比值线性变化；且滤波器滚降系数越大，真实信噪比值变大的程度越大，真实信噪比的值越大。不难理解，发送端的脉冲成型滤波器和接收端的匹配滤波器，都可以对带外噪声进行一定程度的抑制，所以信噪比值会变大。

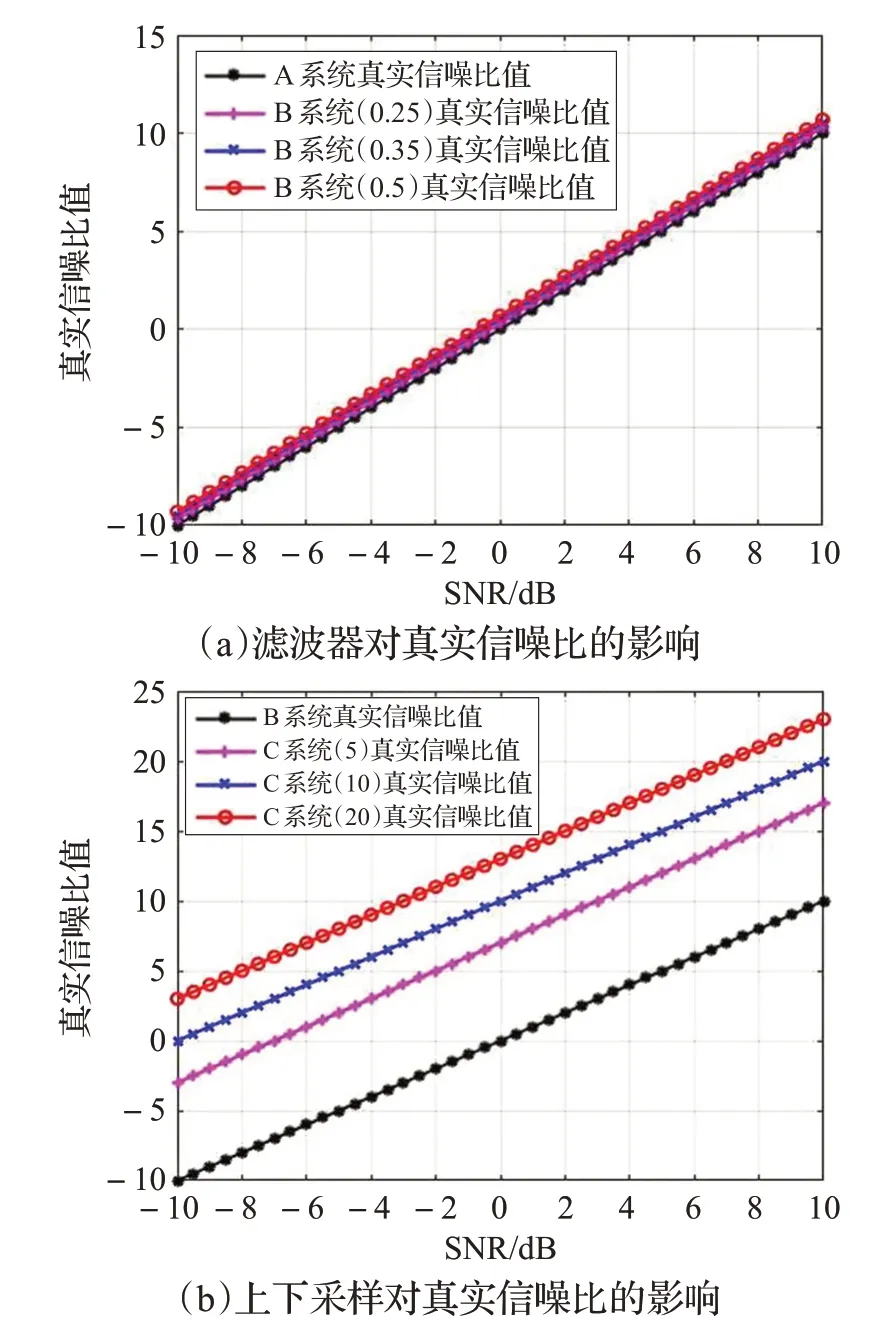
图2 滤波器和上下采样对真实信噪比的影响

观察图2（b），“B 系统真实信噪比值”是系统含有0.35 滚降系数的滤波器但是未进行上下采样情况下的信噪比值，“C系统真实信噪比值”则是既含有0.35滚降系数的滤波器又进行了上下采样情况下的信噪比值。从仿真图中可以看出，上下采样使得真实信噪比值变大；且采样倍数越大，真实信噪比值变大的程度越大，真实信噪比的值越大；同时可以发现，在相同的采样倍数下，不同信噪比其对应的变大的数值是相同的。采样倍数为5、10、20 时，其对应的信噪比增大值大约分别为7 dB、10 dB、13 dB。下采样提高信噪比这种现象其实并不难理解，以常见的数字接收机为例，最后要得到的基带信号其采样率应等于符号速率。然而，通常的做法是，采用比符号速率高得多的采样率对模拟信号进行采样，然后再进行下采样（即抽取），得到速率大小等于符号速率的信号。这样处理可以提高信噪比，信噪比增益即为下采样倍数，如5倍下采样对应的信噪比增益为：

10 ⋅lg 5 ≈ 7 dB （2）

对于提高信噪比来说，下采样起主要作用，上采样则起到匹配下采样的作用。

3.3 滤波器和上下采样对信噪比估计算法的影响

前面研究了滤波器和上下采样对真实信噪比的影响，下面主要研究滤波器和上下采样对信噪比估计算法的影响。要研究其对各个信噪比估计算法的影响，就必然要将信噪比估计模块加到仿真系统里。这里将信噪比估计模块分别加到A、B、C 系统的输出信号位置，也就是使用各个系统的输出信号进行信噪比估计。

将B 系统输出信号的真实信噪比与A 系统输出信号的真实信噪比作比较，可以体现出滤波器对真实信噪比的影响；将C系统输出信号的真实信噪比与B系统输出信号的真实信噪比作比较，可以体现出上下采样对真实信噪比的影响；将A系统输出信号的信噪比估计值与该位置的真实信噪比值作比较，可以体现出在不加滤波器也不加上下采样的情况下，对应信噪比估计算法在A系统输出信号位置的性能；将B系统输出信号的信噪比估计值与该位置的真实信噪比值作比较，可以体现出在经过滤波器但是不加上下采样的情况下，对应信噪比估计算法在B系统输出信号位置的性能；将C系统输出信号的信噪比估计值与该位置的真实信噪比值作比较，可以体现出在既有滤波器又有上下采样的情况下，对应信噪比估计算法在C系统输出信号位置的性能；将B系统输出信号的信噪比估计值与A 系统输出信号的信噪比估计值作比较，可以同时体现出滤波器对真实信噪比的影响以及对相应信噪比估计算法性能的影响；将C系统输出信号的信噪比估计值与B 系统输出信号的信噪比估计值作比较，可以同时体现出上下采样对真实信噪比的影响以及对相应信噪比估计算法性能的影响。

综上，可以分析得到：对于同一信噪比估计算法，将B 系统输出信号位置估计算法的性能与A 系统输出信号位置相应信噪比估计算法的性能作比较，可以体现出滤波器对该信噪比估计算法性能的影响；同样，对于同一信噪比估计算法，将C系统输出信号位置估计算法的性能与B系统输出信号位置估计算法的性能作比较，可以体现出上下采样对该信噪比估计算法性能的影响。这里估计算法的性能是通过信噪比估计值与信噪比真实值之间的偏差来描述的，即信噪比估计值减去信噪比真实值并取平均。

3.3.1 滤波器对信噪比估计算法的影响

首先研究滤波器对算法估计性能的影响。在信道中加入噪声，使A 系统输出位置的真实信噪比在[-10 dB,10 dB]范围内变化，分别计算A系统输出信号信噪比估计值与信噪比真实值之间的偏差，以及B系统在不同滚降系数下的偏差。观察B 系统在不同滚降系数下，输出信号信噪比估计值与信噪比真实值之间的偏差，相比于A 系统发生了哪些变化。以QPSK 调制为例，符号速率为10 MHz，蒙特卡洛仿真50次，非辅助数据算法使用数据长度为50 000（调制前长度），辅助数据算法使用训练序列长度为600（调制后长度），B 系统中的滤波器滚降系数分别为0.25、0.35、0.5 时M2M4、DF、ECF算法的仿真结果如图3所示。

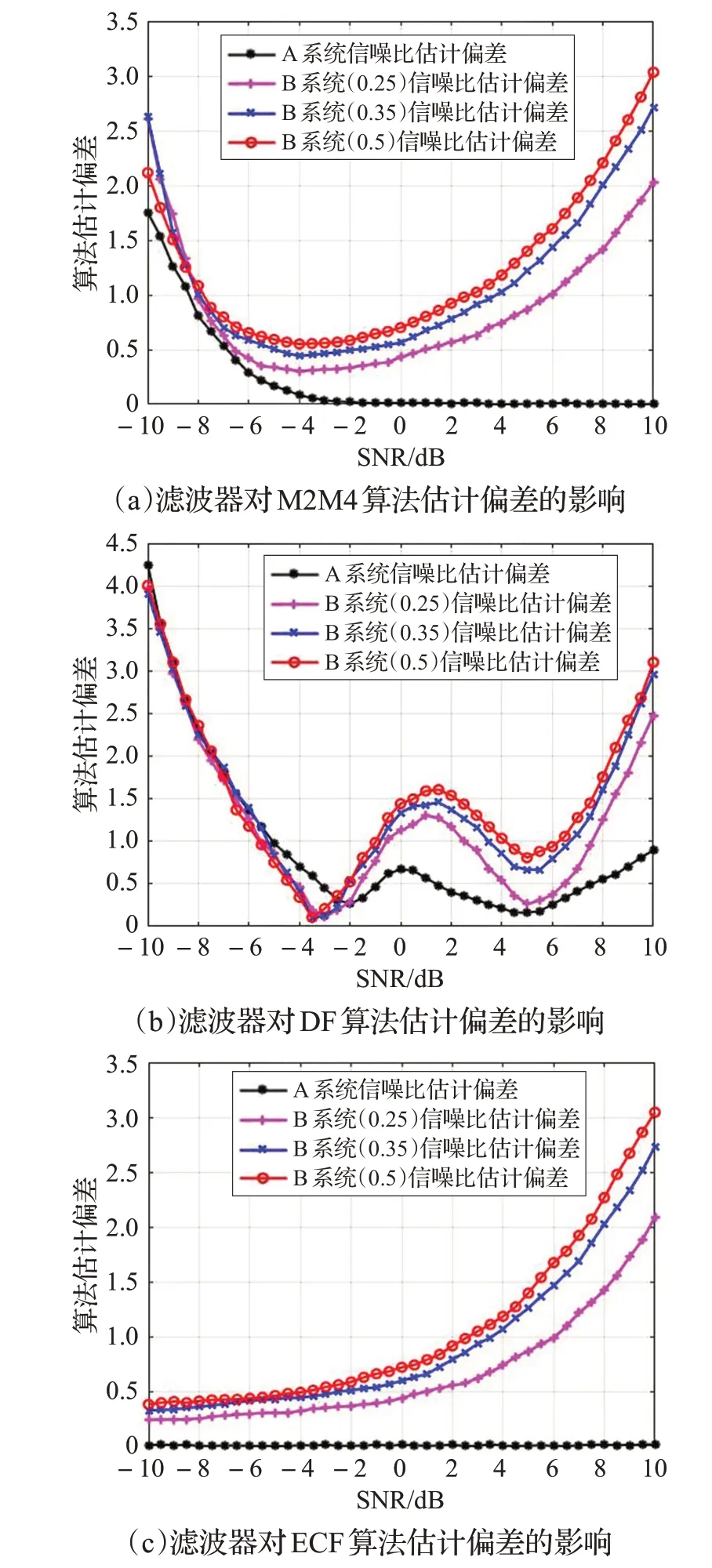
图3 滤波器对M2M4、DF、ECF算法估计偏差的影响

观察图3，对比B 系统估计偏差曲线与A 系统估计偏差曲线，可以发现滤波器使得算法在[-10 dB,10 dB]整个范围内估计偏差的绝对值变大；滤波器滚降系数0.25、0.35、0.5 分别对应着信噪比估计偏差绝对值为“小”、“中”、“大”。这种现象并不难理解。平方根升余弦低通滤波器的传递函数与理想低通滤波器并不完全相同，因此平方根升余弦滤波器的存在势必会改变信号的频域形状，使信号失真。两个平方根升余弦滚降低通滤波器分别位于发送端和接收端，这意味着发送端的信号经过了两个平方根滤波器的作用，而信道中的噪声只被接收端的平方根滤波器作用，即信号与噪声的相对功率可能发生了变化。大多数信噪比估计算法进行建模的时候，并没有考虑这一点，因此，加入滤波器之后算法的估计偏差会变大。且滚降系数越大，这种现象越明显，估计偏差越大。

另外，各个算法的性能对滤波器的敏感程度并不相同。对于各个算法，将经过滤波器的估计偏差曲线（B系统）与未经过滤波器的估计偏差曲线（A系统）进行比较，可以看出，M2M4 算法和ECF 算法在高信噪比下对于滤波器较为敏感，而DF 算法在高低信噪比下均不敏感。这与算法本身的机理有关。

上述分析说明，滤波器确实会对信噪比估计算法的性能产生不良影响，且滚降系数越大影响也越大，不同算法受影响的程度也不同。

3.3.2 上下采样对信噪比估计算法的影响

然后研究上下采样对信噪比估计算法性能的影响（如图4）。在信道中加入噪声，使A系统输出位置的真实信噪比在[-10 dB,10 dB]范围内变化，分别计算B系统输出信号信噪比估计值与信噪比真实值之间的偏差，以及C 系统在不同采样倍数下的偏差。观察C 系统在不同采样倍数下，输出信号信噪比估计值与信噪比真实值之间的偏差，相比于B 系统发生了哪些变化。以QPSK调制为例，符号速率为10 MHz，蒙特卡洛仿真50次，B系统和C系统的滤波器滚降系数均为0.35，非辅助数据算法使用数据长度为50 000（调制前长度），辅助数据算法使用训练序列长度为600（调制后长度），C 系统中的采样倍数分别为5、10、20 时M2M4、DF、ECF 算法的仿真结果。

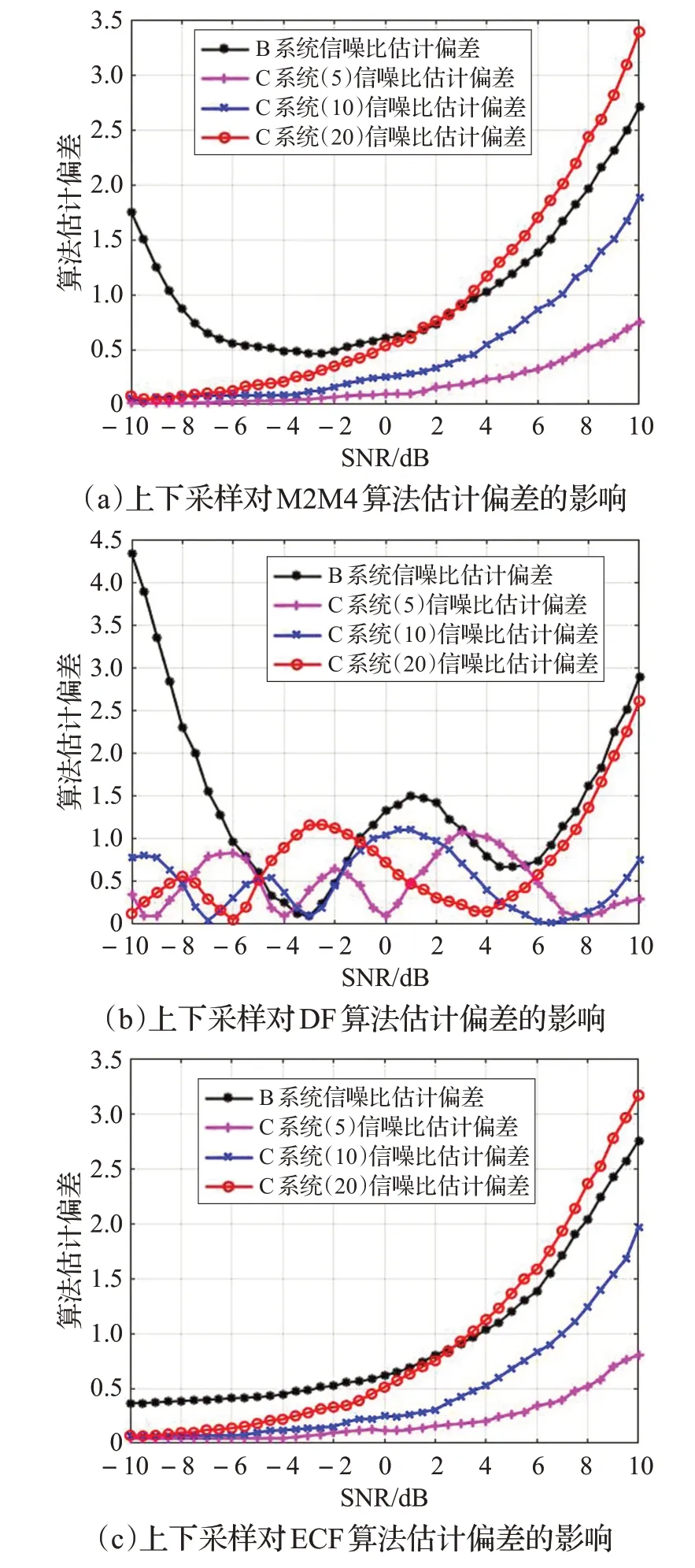
图4 上下采样对M2M4、DF、ECF算法估计偏差的影响

观察图4，对比C 系统估计偏差曲线与B 系统估计偏差曲线，可以发现：低信噪比下，上下采样使得算法估计偏差的绝对值变小；高信噪比下，经过5倍、10倍上下采样的估计算法偏差绝对值仍然比未经过上下采样的估计算法偏差绝对值要小，但是20 倍的上下采样使得算法的估计偏差绝对值比未经上下采样的略大；且采样倍数越小，算法的估计偏差绝对值越小。另外，各个算法对上下采样的敏感程度不同。对于各个算法，将经过上下采样的估计偏差曲线（C 系统）与未经过上下采样的估计偏差曲线（B 系统）进行比较，可以看出，M2M4算法与DF 算法在低信噪比下对上下采样较为敏感，ECF 算法在高低信噪比下均不敏感。这同样是由算法本身的机理导致的。

上述分析说明，上下采样确实会对信噪比估计算法的性能产生影响，且采样倍数较低或信噪比较低的情况下会使得算法的性能变好，不同算法受影响的程度也不同。

3.4 小结

第4 章在含有滤波器和上下采样的仿真系统上对经典信噪比估计算法进行仿真，以得到同时含有滤波器和上下采样的系统上性能较好的信噪比估计算法。为了辅助第4章的工作，第3章首先搭建了三个仿真系统，然后针对滤波器和上下采样对真实信噪比以及信噪比估计算法性能的影响进行了研究。研究结果如表2。

4 经典信噪比估计算法的仿真

以往的文献在对信噪比估计算法进行研究的时候，从未在同时考虑滤波器和上下采样的情况下对算法进行仿真。而滤波器和上下采样又确实会对算法的性能产生影响，且不同算法的性能受滤波器和上下采样影响的程度不同。仿真时同时考虑滤波器和上下采样，将更贴合实际应用的效果，以设计出实际应用中性能优良的信噪比估计方案。

对数据辅助算法（SD、LSE、ML）和非数据辅助算法（M2M4、CUM、M2M4M6、M2M4_QAM、DF、ECF、SVR、JLG、power、优化 power），在 QPSK、8PSK、16APSK(R2/R1=2.84)、32APSK(R2/R1=2.84,R3/R1=5.27)、16QAM 五种调制方式下进行仿真。使用C 系统，滤波器滚降系数0.35，上下采样的倍数为5，符号速率为10 MHz，蒙特卡洛仿真50 次，非数据辅助算法使用数据长度为50 000（调制前长度），数据辅助算法使用训练序列长度为600（调制后长度）。仿真结果如图5～9所示。

观察图5～图9，发现不管是QPSK、8PSK、16APSK、32APSK、16QAM 中的哪种调制方式，信噪比真实值均在[-4 dB,16 dB]范围内，这是因为仿真时经过了5 倍的上下采样，从而使得信噪比真实值与原本的[-10 dB,10 dB]相比大约提升了6 dB。

表2 滤波器和上下采样的影响

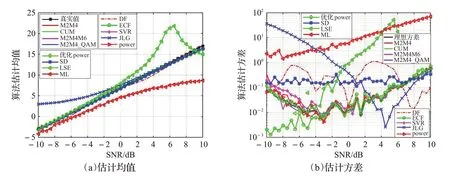
图5 QPSK调制下各算法的估计均值及估计方差

图6 8PSK调制下各算法的估计均值及估计方差

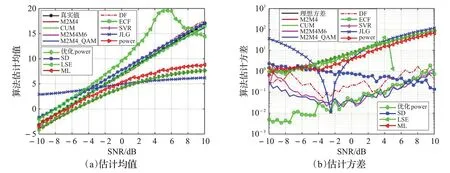
图7 16APSK调制下各算法的估计均值及估计方差

图8 32APSK调制下各算法的估计均值及估计方差

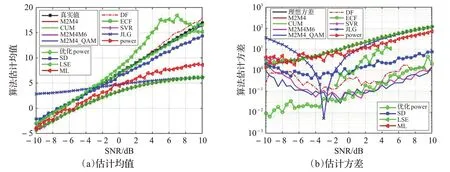
图9 16QAM调制下各算法的估计均值及估计方差

对比观察图5、图6，可以看出，M2M4、CUM、M2M4M6、M2M4_QAM、ECF、SVR、power、优化 power、SD 算法在两种调制方式下的性能均较为优良，估计误差均在0.5 dB以内。

同样，对比观察图7～图9，可以看出，M2M4M6、M2M4_QAM、ECF 算法在两种调制方式下的性能均较为优良，估计误差均在0.5 dB以内。也可以看出，M2M4、CUM、SVR、JLG、power、优化power、ML 算法在这两种调制方式下性能尤为恶劣，结合理论分析其原因是这几种算法仅适用于恒模调制方式。

可以看出，在QPSK、8PSK、16APSK、32APSK、16QAM五种调制方式下效果均较好的是M2M4M6、M2M4_QAM、ECF算法，均较差的是DF、JLG、LSE、ML算法。

另外，在仿真过程中可以发现，算法SD、LSE、ML的信噪比估计结果有出现复数值的可能。分析这些算法的原理，发现这些算法在运算过程中均有对负数值进行开方的可能，这是算法出现复数信噪比估计结果的原因。

5 总结

各种经典的信噪比估计算法，需要的先验知识不同，导致其应用场合也各不相同。特定的场合，对应着能被满足先验知识的信噪比估计算法集合，在这个集合中选择最能满足需要且性能最为优良的信噪比估计算法，或将集合中的几种算法结合使用以弥补相互之间的局限，从而得到性能优良的信噪比估计方案。文献中在对算法性能进行仿真时，考虑的影响因子主要包括数据长度、调制方式等。实际上，在无线通信等的数字信号处理过程中，滤波器和上下采样在系统中非常常见。本文研究了滤波器和上下采样对信噪比及其估计算法性能的影响，为数字信号处理中滤波器和上下采样倍数的设计与选择提供了参考依据。另外，本文还在同时具有滤波器和上下采样模块的仿真系统中，验证了经典信噪比估计算法的性能；比较得到每种调制方式（QPSK、8PSK、16APSK、32APSK、16QAM）下各种估计算法的性能与特点。

从应用来看，信噪比估计需要的是在保证估计性能的情况下，尽可能地实现“数据盲”、“类型盲”以及较低的运算量等，甚至是全盲。这应当是信噪比估计接下来的工作。