三支决策朴素贝叶斯增量学习算法研究

韩素青，成慧雯，王宝丽

1.太原师范学院 计算机科学与技术系，山西 晋中 030619

2.运城学院 数学与信息技术学院，山西 运城 044000

1 引言

1973 年，Duda 和Hart 基于贝叶斯公式首次提出了朴素贝叶斯分类模型（Naïve Bayes Classifiers，NBC），该模型由于实现简单，计算高效，并具有坚实的理论基础而得到广泛应用。近年来，随着数据的爆炸式增长以及流数据的不断涌现，包括朴素贝叶斯算法在内的许多分类算法的泛化性和可扩展性受到了限制。

增量式学习能够利用增量数据中的有用信息通过修正分类参数来更新模型，它有两个显著的特点：（1）无需存储历史数据；（2）能够有效利用之前的训练结果。因此，增量式学习被视为处理大规模数据和流数据的一类有效方法。

贝叶斯学习本身具有增量学习的特性，不仅易于实现增量学习的功能，而且可以有效降低学习算法的复杂性。最早提出的增量贝叶斯学习模型[1]，根据0～1 损失[2]，通过依次加入能够最小化当前分类模型分类损失的样本，以增量方式学习分类参数，并实现对样本的分类。但该算法在增量过程中，易受噪声影响。为此，一些学者对其进行了改进。丁厉华等人[3]以类支持度因子选择增量样本来对分类器进行更新，但该算法降低噪声影响的效果并不明显。罗福星等[4]提出一种加权朴素贝叶斯增量学习算法，该算法基于置信度，动态调整增量样本，具有良好的自适应能力。不过，由于该算法对部分频数较少但却具有较强分类能力的样本的偏好不足，因此可扩展性不强。

姚一豫教授于2010年创立的三支决策理论是符合人类认知模式的一种新型理论。该理论从应用的角度对粗糙集的核心概念正域、负域和边界域给出了合理的语义解释[5-6]。有别于传统二支决策理论只考虑接受和拒绝两种选择，三支决策理论在解决很多问题时，会依据决策可能导致的代价或后果，增加延迟决策这一选择。当信息不足，难以决定接受或者拒绝时，采取延迟决策，不仅可以减少对不确定性知识做出误判，而且能够规避误判所导致的损失，符合人们在决策过程中的思维习惯。

近年来，关于三支决策的研究受到越来越多学者的关注，刘盾等对三支决策理论提出了新的研究方法和应用领域[7]；杜丽娜等将贝叶斯原理和基于决策粗糙集的三支决策规则引入到模糊综合评判中，提出了基于三支决策风险最小化的风险投资评判模型[8]；李华雄等采用代价敏感三支决策方法获得了相应粒度下的最小代价决策[9]；李金海等提出了一种用多粒度描述三支决策概念的公理化方法，并通过数值实验对所提出的学习方法进行了性能评价[10]；郎广名等在决策粗糙集理论的基础上，提出了动态信息系统中概率冲突集、中性集和联合集的增量构造方法[11]；此外，李金海等还对概念格与三支决策相结合的研究进行了一定的探讨及展望[12]。

由于三支决策粗糙集模型倾向于关注分类错误带来的风险代价，因此是具有代价敏感性数据分析的有效工具[13]。此外，三支决策理论中损失函数的确定需要先验信息和专家知识，存在一定的主观能动性，与朴素贝叶斯学习的客观性某种程度上形成了互补。

本文将三支决策思想融入朴素贝叶斯增量学习中，提出一种基于三支决策的朴素贝叶斯增量学习算法。首先，为防止有用信息过早损失，利用朴素贝叶斯算法得到的最大后验概率和次最大后验概率构造了一个称为分类确信度的评价函数，用以确定三支决策理论中的正域、负域和边界域。然后算法以迭代方式进行，每一次迭代都用由正域、负域中的误分类样本、边界域中的样本以及新增样本构成的数据集重新训练朴素贝叶斯分类器，直到算法结束。三支决策思想的引入和增量学习机制的构建，旨在使算法的分类正确性和召回率获得明显提高。

2 基本概念

2.1 朴素贝叶斯分类模型

朴素贝叶斯模型结构简单、计算高效、易于阐释且应用广泛。但该模型需要一个很强的条件保证，即需要假定描述数据的各个属性对于给定类的取值相互独立，即任何属性的取值不依赖于其他属性。

假定数据集D包含m个条件属性，记作A1,A2,…,Am；以及t个类，记作C1,C2,…,Ct。训练样本X表示为一个m维特征向量，即X={x1,x2,…,xm} ，其中xi表示样本关于条件属性Ai的值，则贝叶斯原理描述如下：

其中，P(Ci)为代表各类样本在样本集中所占比例的先验概率；P(X|Ci)为样本X相对于类Ci的条件概率；P(Ci|X)为样本X属于类Ci的后验概率；而P(X)是则是用于归一化的“证据”因子。

给定样本X，朴素贝叶斯分类器将X预测为具有最大后验概率P(Ci|X)的类，即朴素贝叶斯分类器将样本X分配给类Ci，当且仅当：

在贝叶斯公式（1）中，由于分母P(X)与类标号的取值无关，因此在确定类别时可以作为常数处理。这样最大化后验概率P(Ci|X)的计算就可以转换为P(X|Ci)P(Ci)的计算。于是，根据朴素贝叶斯分类的条件独立性假设可得：

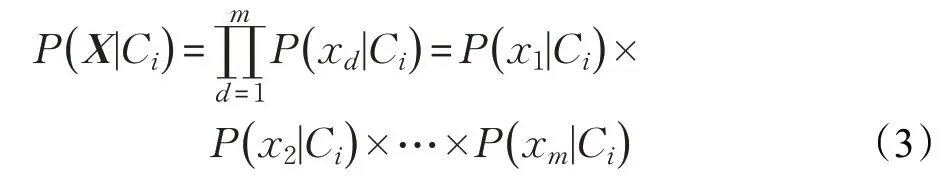
其中，P(x1|Ci)×P(x2|Ci)×…×P(xm|Ci)可以从数据集中求得。于是，朴素贝叶斯分类模型描述为：

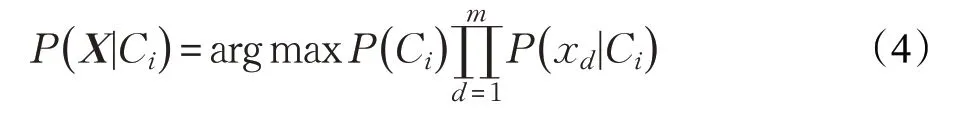
2.2 朴素贝叶斯增量学习算法

增量分类学习的实质可以归结为根据先验知识和增量信息来确定先验概率P(Cj)和条件概率P(X|Cj)。增量式贝叶斯分类主要针对增量样本集T={T1,T2,…,Tr}进行处理，可以分两种情况进行讨论。

（1）增量集T中的每一个样本都拥有类别标签。这种情况下，增量学习先用当前分类器对T中的样本进行测试，并将测试结果与其本身的类别标签进行对比，若结果一致，则保持当前分类器不变；否则用新增样本修正当前分类器。

（2）增量集T中的每一个样本都没有类别标签，需要先用当前分类器为每个样本分配类标签，然后再利用其含有的有用信息更新当前分类器。

无论是情况（1）还是情况（2），增量学习更新分类参数都应当从增量集T中优先选择能够有效提升分类器精度的有价值的样本。

假定朴素贝叶斯增量学习采用0～1 损失[2]度量性能，并假定增量样本Tp(Tp∈T,p=1,2,…,r)根据朴素贝叶斯分类器获得的类标签为(p=1,2,…,r)，则根据文献[1]：

算法1一种增量贝叶斯分类模型[1]

输出：增量贝叶斯分类器C。

步骤1利用训练集D，学习朴素贝叶斯分类器C。

步骤2如果T=φ，返回朴素贝叶斯分类器C；否则转步骤3。

步骤3令分类损失l=0，对增量集T中的每一个样本Tp∈T，重复以下步骤：

（1）利用现有分类器C、分类Tp，获得Tp的类标签。

（3）如果L＞l则。

步骤4。

转步骤1。

上述增量贝叶斯分类模型有两个点非常关键：一是对增量样本进行分类；二是基于新增数据后的数据集计算类概率P∗(Ci)：

和类条件概率P∗(xjd|Ci)：

其中，在式（6）中，μ=|C|+|D|，|C|为类别数，|D|为训练样本的大小。在式（7）中λ=|Aj|+count(Ci)，|Aj|为属性Aj取值的个数，count(Ci)是类别为Ci的样本个数，xjd为属性Aj的第d个取值。

2.3 三支决策

姚一豫教授提出的三支决策理论[6，14-15]研究的最初目的是为粗糙集的三个域提供合理的语义解释。他将粗糙集中的正域、负域和边界域分别对应于决策中的接受、拒绝和不承诺。具体而言，正域对应于可以接受的决策，负域对应于应当拒绝的决策，而边界域则对应于不承诺的决策。做出接受、拒绝或不承诺三种决策需要考虑决策所导致的风险或代价[2]。在三支决策理论中，决策的代价函数或风险函数可以作为评价函数用于确定三支决策理论中的正域、负域和边界域。因此，三支决策理论中的正域、负域和边界域与代价函数或风险函数密切相关。

假定D是一个有限、非空的样本集或决策方案集，A是由有限个条件组成的条件集，其中条件集可能包含指标、目标或约束。决策的主要任务是根据给定的条件集A，对每个样本X∈D做出决策。

如果令α和β(β＜α)是以样本的某个决策风险函数或决策代价函数为评价函数获得的阈值，那么对于给定的条件集A，三支决策理论针对D中样本满足给定条件的程度，可以处理D中样本的分类问题，并作出合理的决策[7]：

（1）如果样本X满足给定条件的程度大于或等于阈值α，那么认为该样本符合给定的条件，应做出接受的决策。

（2）如果样本X满足给定条件的程度小于或等于阈值β(β＜α)，那么认为该样本不符合给定的条件，应做出拒绝的决策。

（3）如果样本X满足给定条件的程度介于α和β之间，那么认为该样本难于判断是否符合给定的条件，应做出不承诺的决策。

于是，基于确定的阈值α、β(β＜α)，所有样本可以根据其评价函数值的大小被划分到三支决策理论的正域、负域或边界域中。

3 基于三支决策的朴素贝叶斯增量学习算法

朴素贝叶斯增量学习算法，对于样本的类别通常有明确的判断，但是在实际情况中，经常会有因各种因素难于对样本类别进行明确判断的情况出现，本章将三支决策思想应用于一般朴素贝叶斯增量算法中，研究基于三支决策的朴素贝叶斯增量学习算法。

基于三支决策的朴素贝叶斯增量学习算法的主要思路如下：

在判别信息不足，难于将待分类样本正确分类时，利用三支决策思想，先把这些样本划分到边界域中，等判别信息量足够时，再将待分类样本正确分类到所属类别中。

3.1 分类确信度

朴素贝叶斯分类方法基于最大后验概率对样本进行分类，也就是说，对于待分类样本，朴素贝叶斯算法根据其最大后验概率确定其类别标签CNB。

对于待分类样本X，在其所有类别的后验概率中，如果最大后验概率和次最大后验概率的值非常接近，那么可以认为，将样本X赋予最大后验概率所确定的类别的确信度不足。基于这种考虑，分类确信度定义如下。

定义1分类确信度。给定训练集D，由训练集D得到的朴素贝叶斯分类器记作NBC,则对于任意X∈D，样本X属于其最大后验概率所确定类别的分类确信度为：

其中，P(yfirst|X,NBC)和P(ysecond|X,NBC)分别为样本X根据朴素贝叶斯分类器获得的最大后验概率和次最大后验概率。

这里，将最大后验概率和次最大后验概率的差值与最大后验概率作比是为了将分类确信度的值归一化到0～1之间。

易知，样本X属于其最大后验概率所确定的类别的分类确信度Ccertainty越大，样本X被正确分类的可能性越大。

3.2 基于分类确信度的正域、负域和边界域

本节以3.1 节定义的分类确信度Ccertainty为评价函数定义训练集的正域、负域和边界域，阈值(α,β)根据所有样本的分类确信度确定。于是，对于确定好的阈值(α,β)，训练集D′⊆D的正域、负域和边界域的判别规则可定义如下：

（1）若Ccertainty(X)≥α，则X∈POS(D′ )；

（2）若β ＜Ccertainty(X)＜ α，则X∈BND(D′ )；

（3）若Ccertainty(X)≤β，则X∈NEG(D′ )。

下面给出基于三支决策的朴素贝叶斯的边界域的提取算法。

算法2基于分类确信度的边界域提取算法

输入：训练集D={X1,X2,…,Xn} ，训练集D的类别Cj(j=1,2,…,t)，阈值参数α和β。

输出：D中基于分类确信度的边界域EB。

步骤1在D上训练朴素贝叶斯分类器NBC。

步骤2对D中的每一个样本Xi(i=1,2,…,n)重复：

（1）对j=1,2,…,t，根据NBC计算其后验概率P(Cj|Xi)。

（2）根据公式（8）计算其分类确信度Ccertainty(Xi)。

步骤3确定阈值(α,β)。

步骤4根据阈值α和β，确定D中的边界域EB。

步骤5输出EB。

步骤6算法结束。

3.3 基于三支决策的朴素贝叶斯增量学习算法

在对有类别标签的数据集进行学习并更新分类器时，文献[16]认为被当前分类器错分的样本中蕴含着比分对的样本更多更有用的信息。因此将基于分类确信度确定的正域、负域中的误分样本通过类别标签索引[17]分别提取并作为增量数据使用，有助于分类器性能的提升。

算法3基于三支决策的朴素贝叶斯增量学习算法

输入：训练集D，随机等分为N个互不相交的子集Di(i=1,2,…,N)。

输出：基于样本集D的朴素贝叶斯分类器Γ。

步骤1取训练集D1进行训练，得到初始的朴素贝叶斯分类器NBC1。

步骤2根据算法2，以及阈值α和β，找出训练集D1中的边界样本集EB1。

步骤3通过类标签索引提取D1中对应的正域、负域中的误分样本MC1。

步骤4将EB1、MC1和子集D2的并集作为新的训练样本训练新分类器NBC2。

步骤5重复步骤2，将得到的新的EBi、MCi和子集Di+1合并训练，如此循环，直至获得由EBN-1、MCN-1与DN训练所得到的NBC，并将其作为最终分类器Γ输出。

步骤6算法结束。

该算法主要利用三支决策思想具有代价敏感性的优势，通过引入一种分类确信度作为评价函数进行三支决策划分，采取比一般朴素贝叶斯增量算法更加谨慎的态度，避免了有用信息的过早损失。

3.4 算法时间复杂度分析

对于算法1 所示的一种增量贝叶斯分类模型的时间复杂度主要取决于朴素贝叶斯分类学习模型的训练和分类损失的计算。在步骤1中，训练集的时间复杂度为O(smt)，其中s为训练样本数，m为属性数，t为类别数。在步骤3中，由于朴素贝叶斯增量学习可以利用原始的训练结果，故增量样本集的时间复杂度为O(hr2mt)，其中h为属性取值的最大个数，r为增量集的个数。所以算法1的时间复杂度为O[(s+hr2)mt]。

对于算法2 所示的基于分类确信度的边界域提取算法的时间复杂度主要取决于朴素贝叶斯分类学习模型的训练和分类确信度的计算。即主要取决于步骤2，故训练集的时间复杂度为O(nmt)，其中n为训练样本数，m为属性数，t为类别数。所以算法2 的时间复杂度为O(nmt)。

对于算法3 所示的基于三支决策的朴素贝叶斯增量学习算法的时间复杂度主要取决于朴素贝叶斯分类学习模型的训练和算法2 中对边界域的提取。该算法将训练集随机等分为N个互不相交的子集，并假设每个子集的个数为k。在步骤2中，需要对每个子集计算其类概率P(Cj)以及类条件概率P(Cj|Xi)，因此其时间复杂度为O(kmt)，其中m为属性数，t为类别数。因此算法3的时间复杂度为O(Nkmt)。

经分析可知，虽然本文提出的算法3中边界域的样本数由阈值α、β确定，但训练集中对应的正域、负域中的误分样本是通过类标签索引提取的；而算法1中分类损失的计算是一个循环的过程。因此，一般情况下，对于确定的阈值α、β，本文提出的算法3会比算法1的时间复杂度在一定程度上有所降低。

4 实验设计与结果分析

4.1 实验数据与实验环境

实验数据使用UCI 数据库中[18]如表1 所示的数据。实验环境为：IntelLenovoi7-4790CPU，4 GB 存储，Windows 7系统，Matlab 2014aMyEclipse。

表1 实验使用的UCI数据集

4.2 实验设计及结果分析

实验需要先对所选数据集进行预处理，当存在缺失值的样本在整个数据集中占比很小的，从数据集中删除存在缺失值的样本，当存在缺失值的样本在整个数据集中占比较大时，采用均值填充法对缺失值进行处理。实验过程中，为保证评估结果稳定可靠，每个数据集都调用随机函数将其随机划分为两个部分：第一部分由80%的数据构成，作为训练数据集使用。使用过程中，这部分数据又被平均分成5 份依次进行增量学习。另一部分由其余20%的数据构成，作为测试数据使用。

实验采用5折交叉验证，通过交替对换训练集与测试集实现，并以5次实验结果的均值作为终值使用。

注解：（1）由于训练集不完备会造成后验概率出现0的现象，故实验过程中采用拉普拉斯对数据进行了平滑修正。（2）本文提出的算法与阈值参数α、β的选择相关，其值通常介于[0，1]之间，需要根据具体问题通过选择相应的损失函数获得[14-15，19-25]。

为分析α、β取不同值时对应结果的变化，本文在[0，1]之间以 0.1 为渐进度选取不同的α和β进行实验。实验结果根据分类准确率和召回率进行评价。

分类准确率记作CA，定义如下：

其中，a表示测试数据集中被正确分类的数据个数，Ntest表示测试数据的总数。

召回率记作recall，是待测试数据集中某类样本被正确分类的样本数与该类所有样本数的比值，即

其中，yi表示样本xi的实际类别，f(xi)为分类器，是分类器f(xi)对测试样本xi的分类结果，I(⋅)为示性函数，count(yi)为测试集中类别为yi的样本总数。

对于示性函数I(⋅)，如果f(xi)=y′i且y′i=yi，则示性函数的取值为1，否则取值为0。

首先，针对分类准确率，基于表1所示数据，比较基于三支决策的朴素贝叶斯增量学习算法与本文算法1所示的一种增量贝叶斯分类模型的测试结果。

基于三支决策的朴素贝叶斯增量学习算法关于表1所示9 个数据集在不同α、β阈值参数下的实验结果如图1～图9所示。其中，α的取值为X轴，β的取值为Y轴，分类准确率为Z轴。

由图1～图9可知，当α≤β时，即当α与β的取值位于X正半轴与Y正半轴所形成区域45°对角线的左半部分时，样本集中不存在边界样本，所以基于三支决策的朴素贝叶斯增量学习算法的测试结果与一种增量贝叶斯分类模型的测试结果相同。当α ＞β时，即当α与β的取值位于X正半轴与Y正半轴所形成区域45°对角线的右半部分时，边界域存在，此时基于三支决策的朴素贝叶斯增量学习算法的测试结果与一种增量贝叶斯分类模型的测试结果相异，具体情况分析如下。

为描述简单，下面将算法1所示的一种增量贝叶斯分类模型记为算法A，本文提出的基于三支决策的朴素贝叶斯增量学习算法记为算法B。

由图1～图3可知，当α ＞β时，边界域存在，此时，关于数据集 Breast-cancer、Haberman's Survival 和 Bupa，算法B 的分类准确率总体上优于算法A 的分类准确率。说明在α、β取值合适的情况下，可以保证算法B优于算法A。

图1 Breast-cancer数据集测试结果

图2 Haberman's Survival数据集测试结果

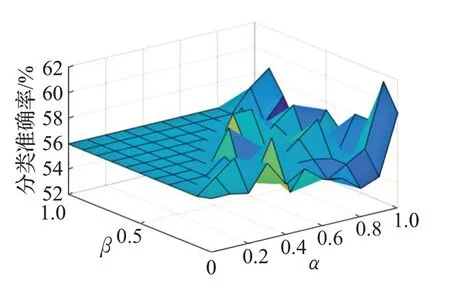
图3 Bupa数据集测试结果

图4 Balance-scale数据集测试结果

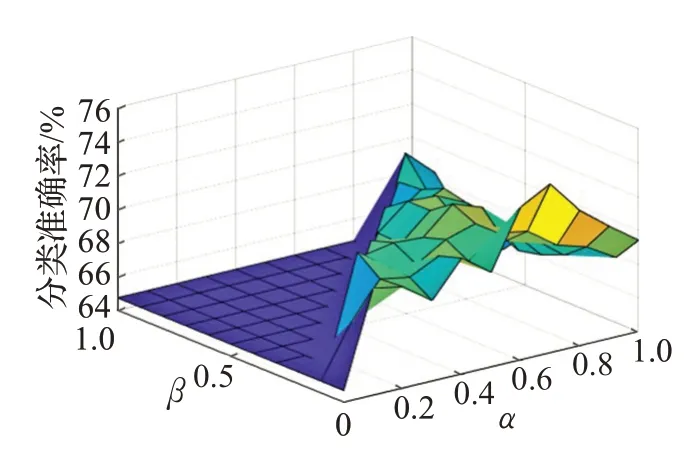
图5 Tic-Tac-Toe数据集测试结果

图6 Contraceptive Method Choice数据集测试结果

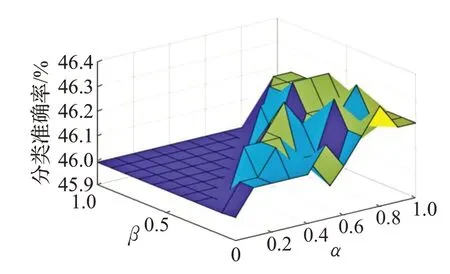
图7 Mammographic Mass数据集测试结果

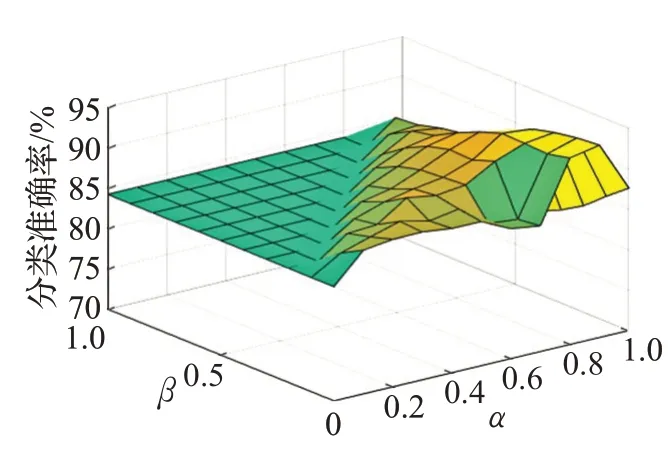
图8 Chess（KR-VS-KP）数据集测试结果

图9 Dermatology数据集测试结果

由图4～图7可知，当α ＞ β时，边界域存在，此时，关于数据集Balance-scale、Tic-Tac-Toe、Contraceptive Method Choice 和 Mammographic Mass，算法 B 的分类准确率全部大于算法A 的分类准确率，说明只要α、β满足α ＞β，算法B 就一定优于算法 A。

由图8可知，当α ＞β时，边界域存在，此时，关于数据集Chess（KR-VS-KP），算法 B 的分类准确率总体上优于算法A 的分类准确率，且分类准确率大多集中在90%左右。特别地，当α取0.9，β取0时，分类准确率高达93.84%，比算法A 提高了9.64 个百分比。说明在α、β取值合适的情况下，可以保证算法B远远优于算法A。

由图9可知，当α ＞β时，边界域存在，此时，关于数据集Dermatology，算法B 的分类准确率均优于算法A的分类准确率，特别地，当α取1.0，β取0.2 时，分类准确率高达98.05%，比算法A 提高了6.69 个百分比。说明在α、β取值合适的情况下，也可以保证算法B 远远优于算法A。

表2是选取不同α、β值时，算法A 和算法B 分类准确率的对比结果。结果进一步显示，在α、β值选择合适时，相较于算法A，算法B的分类准确率有了明显的提高。

面对实际问题时，α和β需要针对具体问题选择合适的评价函数来求得相应的阈值。

综上所述，当α ＞ β，且α和β的取值合适时，本文提出的基于三支决策的朴素贝叶斯增量算法的分类准确率明显优于算法1所示的增量贝叶斯分类模型。

其次，由于数据集类别不平衡现象普遍存在，因此仅用分类准确率来衡量模型的性能可能存在片面性，因此基于召回率，根据表1 所示数据集，本文对算法A 和算法B 进行了二次比较分析。

在表1 所示数据集中，Breast-cancer、Haberman's Survival、Balance-scale 和 Dermatology 是 4 个不平衡数据集，图10～图13是算法B 基于4个数据集在不同阈值参数下的实验结果，其中α的取值为X轴，β的取值为Y轴，分类召回率为Z轴。

观察图10～图13易知，当α≤β时，数据集中不存在边界样本，故算法B 的召回率与算法A 的召回率相同；当α ＞β时，数据集中存在边界样本，且当α、β取值合适时，算法B 关于每个数据集的各个类别的召回率均比算法A 高。

表2 分类准确率对比 %

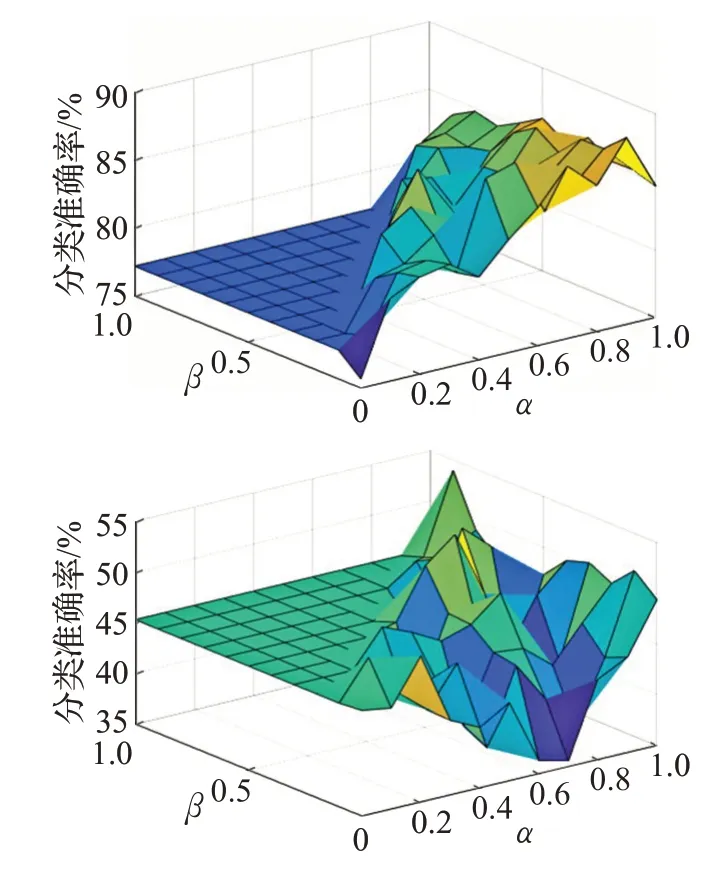
图10 Breast-cancer类别1-2的召回率

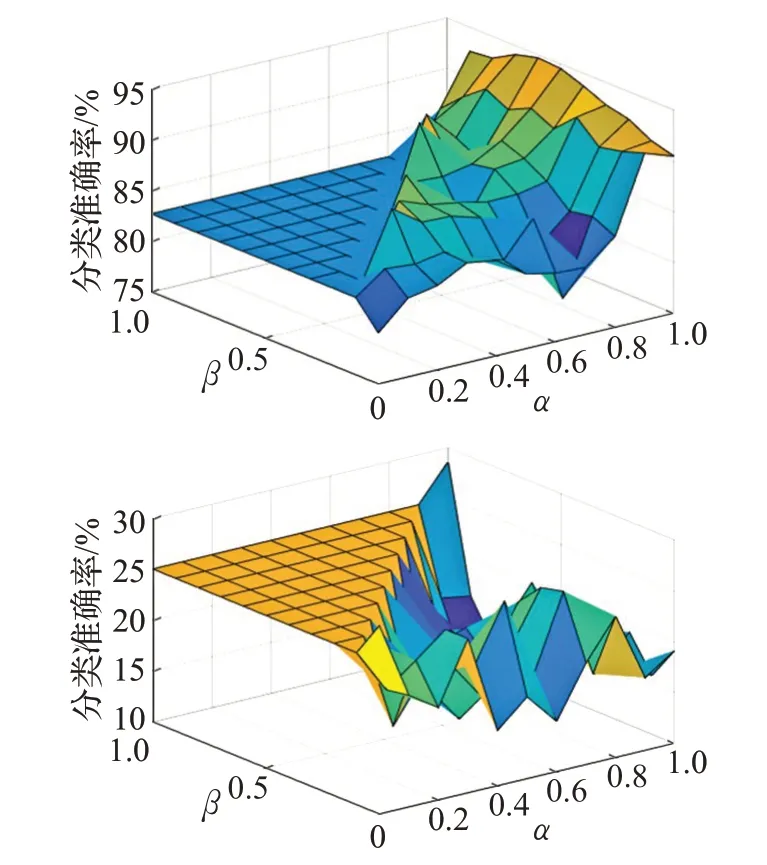
图11 Haberman's Survival类别1-2的召回率

图12 Balance-scale类别1-3的召回率

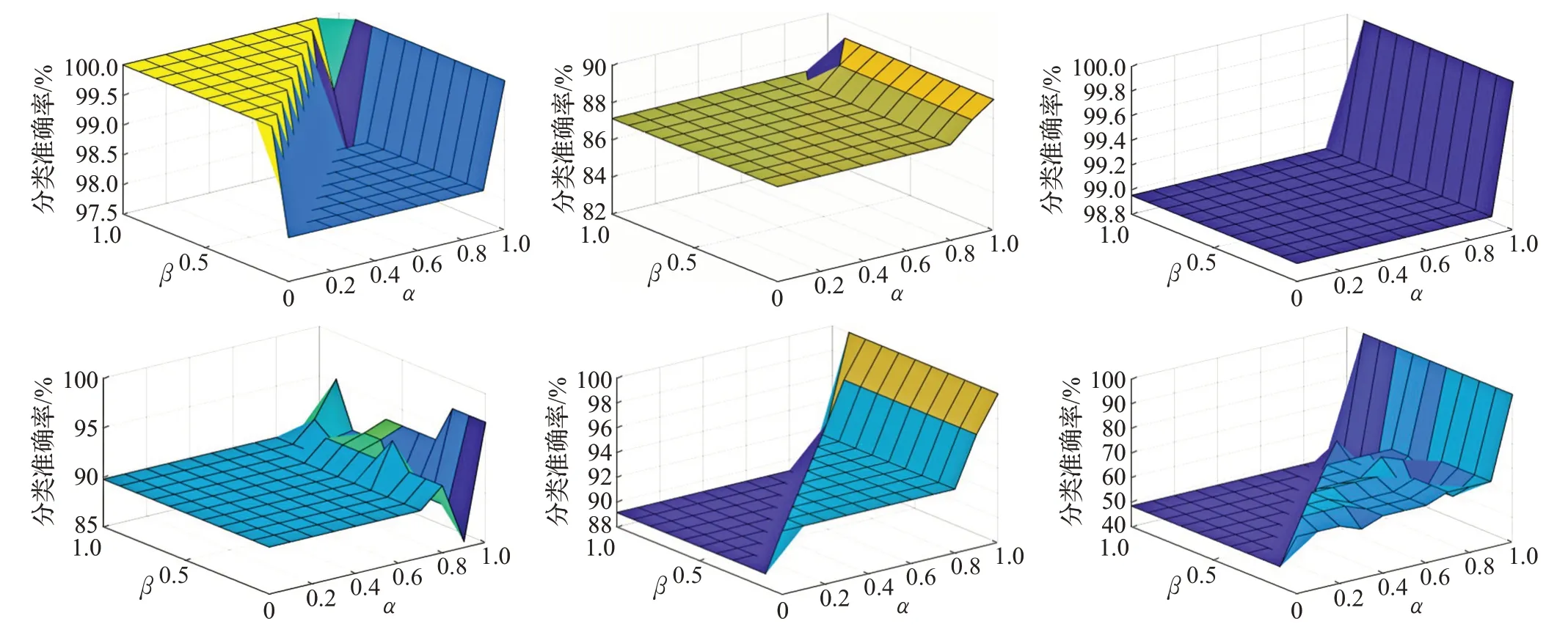
图13 Dermatology类别1-6的召回率

表3 是算法A 与算法B 基于不同的数据集和不同α、β取值的召回率对比结果，其中，对于数据集Breastcancer，阈值α、β分别取0.7和0.5；对于数据集Haberman's Survival，阈值α、β分别取0.5和0.1；对于数据集Balancescale，阈值α、β分别取0.4和0；对于数据集Dermatology，阈值α、β分别取1和0.6。结果显示，在α、β值选择合适时，相较于算法A，算法B的分类召回率也有明显的提高。

5 结束语

本文将三支决策理论融入一般朴素贝叶斯增量算法中，基于二者优势构建了一种基于三支决策的朴素贝叶斯增量学习算法。首先，利用最大后验概率和次最大后验概率定义了一个称为分类确信度的概念，用以度量分类的准确程度，然后结合代价函数，给出了确定三支决策理论中正域、负域和边界域的规则；其次，利用朴素贝叶斯学习理论本身具有的增量学习特性，通过将三支决策正、负域中的错分样本和边界域中的样本作为增量数据，以增量方式更新模型参数，在提升算法性能的同时，使算法具有了代价敏感性。

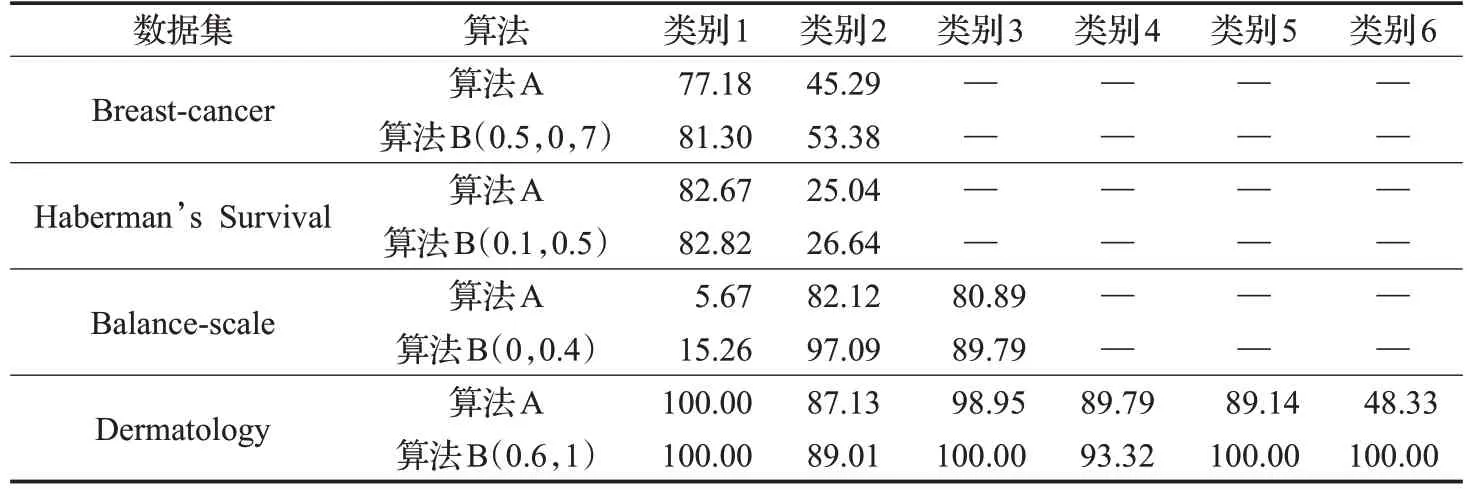
表3 召回率对比 %

最后，利用UCI数据库中的9个数据集对所提算法进行了实验，并与文献[1]提出的一种增量贝叶斯分类模型进行了实验对比。实验结果显示，本文提出的基于三支决策的朴素贝叶斯增量学习算法可行且有效。不过，针对实际问题，基于三支决策理论的正区域、负区域和边界域的更有效确定方法、增量学习的更有效机制，以及增量学习算法性能的进一步提升将是下一步需要探究的问题。