带有动态爆炸半径的增强型烟花算法

张水平，李殷俊，高 栋，梁 文

江西理工大学 信息工程学院，江西 赣州 341000

1 引言

群体智能是进化计算中的活跃分支，包括基于生物和非生物的优化算法。烟花算法便是模拟烟花的爆炸结合进化计算的随机搜索而产生的新型搜索算法，由Tan等[1]于2010年提出。

此后，许多改进算法相继被提出[2-11]并总结了研究进展[12]。Pei 等[13]提出基于适应度函数估计的加速型烟花算法，使用种群的适应度值信息估计搜索空间的形状，将形状最优位置作为启发式信息进行加速搜索，相比烟花算法基于距离信息的估计在性能加速方面有一定提升。Zheng 等[14]提出增强烟花算法，对算法存在的缺陷进行逐一改进，重在将轮盘赌方法改为精英-随机选择策略，减少了算法的时间消耗。Liu 等[15]提出自适应烟花算法，通过最优个体和一个特定个体间的距离计算新的爆炸半径，加强了算法的局部搜索能力。以上改进算法均只对烟花算法的部分进行强化，本文则对各个组成进行详细分析做出改进，相比基本烟花算法有了全面的提升。

现有改进研究采用的测试函数，其最优值在原点或原点附近，由于烟花算法映射规则和变异算子加强了原点附近的搜索，所以算法易于求解原点附近的最优值；若优化函数的最优值远离原点，则烟花算法表现出较差的性能。为了减少烟花算法的缺陷，本文在整体提升的基础上引入动态调整爆炸半径的策略来加强局部搜索及跳出局部收敛的能力，同时提高算法搜索精度。通过实验验证了所提出算法的有效性。

2 烟花算法

FWA（Fireworks Algorithm）模拟烟花爆炸的现象，通过初始的N个烟花经历爆炸和变异生成新的火花，采用映射规则爆炸保证所有火花在可行域内，基于欧式距离从烟花和火花中选择新一代的N个烟花。开始迭代直到满足问题的精度或者达到最大函数评估次数。

2.1 算法框架

烟花算法的执行流程图如图1所示。

图1 烟花算法执行流程图

具体实现包括以下步骤：

（1）在给定的解空间内随机产生N个初始烟花，每个烟花表示解空间内的一个解。初始烟花集合X=[x1,x2,…,xN]，烟花的维度为D。

（2）根据适应度函数计算每个烟花的适应度值f(xi)，通过f(xi)计算每个烟花的爆炸半径Ai和爆炸数量Si，进而产生爆炸火花。爆炸半径集合A=[A1,A2,…,AN]，每个烟花爆炸的数量集合S=[S1,S2,…,SN]，产生的火花集合Y=[yi1,yi2,…,yij,…,yiSi]，其中i∈[1,N]，j∈[1,Si]。烟花爆炸半径的计算公式为：

产生火花数量的计算公式为：

其中，m是一个常数，用来限制火花数量的最大值，Ymax是当前种群适应度值最优的结果，参数ε的含义与式（1）等同。

火花数量的限制计算公式为：

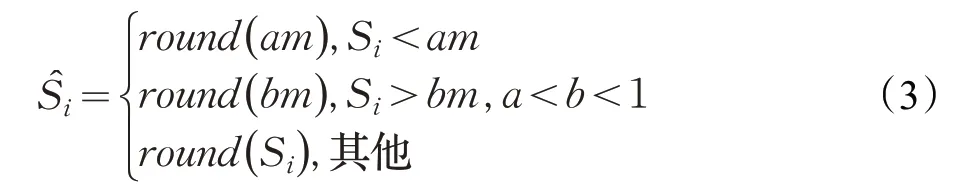
其中，round()是取整函数，a和b是给定的常数。

烟花位移产生火花的计算公式为：

（3）对部分烟花进行高斯变异，变异火花的集合G=[G1,G2,…,Gi]，计算公式为：

其中，gs是服从均值和方差都为1 的高斯分布的随机数，×是乘运算。

对超出边界的火花采用映射规则，计算公式为：

其中，是第k维的上界是下界，%是模运算。

（4）烟花和火花的总集合C={X⋃Y⋃G}从C中选择N个个体作为下一代的初始烟花。采用欧式距离计算两个个体间的距离，计算公式为：

其中，xi和xj表示集合C中任意两个个体。Dis(xi)是个体xi与其余个体的距离总和。

采用轮盘赌计算选择的概率，计算公式为：

（5）循环步骤（1）～（4），直到满足终止条件。

2.2 烟花算法分析

算法的爆炸半径和爆炸火花数量根据式（1）和（2）得到，可以看出适应度值越差，生成的爆炸半径越大，由此产生的火花数量越少，因此扩大搜索范围，增加个体多样性；适应度值越好，生成的爆炸半径越小，产生的火花数量越多，从而缩小搜索范围。这样的火花产生机制并不能确保烟花种群的多样性，因为大范围的火花数量过少，在选择机制中可能无法被选上。

通常测试函数的全局最优点在原点、搜索空间的上下边界对称且超出边界的都是一个很小的值，这种映射规则会使得超出边界的点被人为设定到原点位置附近，从而无意中加速了算法的收敛性。假设目标函数的搜索范围是[-10,10]，当火花在第k维度上的位置上是11，即超过边界时，根据式（6）该维度会被映射到yikj=-10+|11|%(20)=1，这距离原点很近。同时，高斯变异算子也容易将解变异到原点位置附近，当随机产生的服从高斯分布的随机变量g接近0时，高斯变异烟花的位置就会接近于0，并且后期难以跳出，这就导致许多变异烟花的位置靠近原点。因此一个解的位置如果已经十分接近原点位置，那么高斯变异将很难使得该点的位置跳出原点位置附近的区域，易陷入局部最优。

3 动态爆炸半径的增强烟花算法

在分析各个算子后提出了不同于EFWA（Enhanced Fireworks Algorithm）的改进算子，并引入动态爆炸半径机制，控制搜索范围的变化，避免算法陷入早熟并提高寻优结果的精度。具体改进如下。

3.1 烟花种群初始化的改进

图2 初始种群过于集中的烟花爆炸图

烟花算法中种群初始化采用随机策略，若初始化的解过于集中，如图2 所示，那么搜索前期将浪费较多的资源进行局部搜索；若初始化的解比较分散，则图3 是前期所期望进行的全局搜索。因此将整个解空间N等分，N=5，每一部分随机生成一组解以确保前期的全局范围。因为烟花种群数N的设定很小，所以无需采用混沌初始化等方法，这样调控会带来在可接受范围内的小幅度的计算开销。图4 是5 等分下的种群示意图，烟花在爆炸范围内产生下一代火花，避免可能存在的初始解过于集中的问题，也更加符合期望的先全局后局部的搜索策略。

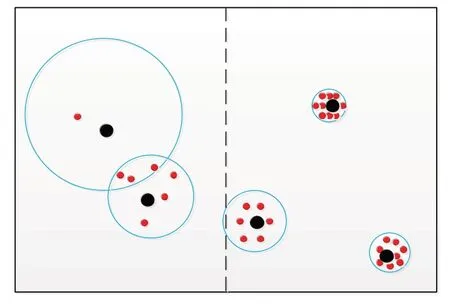
图3 期望种群初始化下的烟花爆炸图

图4 解空间5等分下的烟花爆炸图

3.2 对变异算子的改进

由于高斯变异(xij=xijg)在当前位置和原点之间产生火花，容易将解变异到原点位置附近，故将高斯变异改为随机变异，公式如下：

其中，g是一个高斯分布的随机变量，xij是第i个烟花在第j维上的位置，是第i个烟花在第j维上的下界，是第i个烟花在第j维上的上界，rand(0,1)是0到1之间均匀分布的随机数。

3.3 对映射规则的改进

当一个火花在某一维度上超出边界，可以通过映射规则将其映射到一个新的位置，同高斯变异一样，FWA的映射规则容易将解映射到搜索空间原点附近的位置，故将其改为随机映射规则，即

其中，XUB,k和XLB,k分别表示该优化问题的上边界和下边界，U( 0,1) 是在[0，1]区间上的均匀随机分布随机数。

3.4 对选择策略的改进

在基本烟花算法中，采用的是基于欧式距离的轮盘赌的方法，但这种方法比较耗时，于是提出了一种双精英-锦标赛选择策略。竞标赛方法相比轮盘赌所需时间更少，为了提高个体的多样性，除了首先选择欧式距离最大的个体以外，也保留了最优适应度值的个体，即为双精英保持策略。接着对剩下的烟花采取锦标赛方法，从烟花和火花的总集合C={X⋃Y⋃G}中随机选择5个个体，再选择其中最优的个体进入下一代种群直至达到原来的种群规模，即

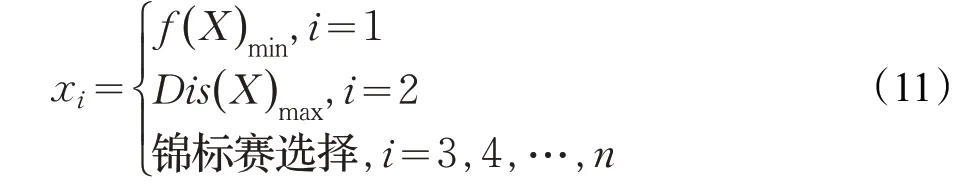
其中，f(X)min是集合X中最小适应度值，Dis(X)max是最大欧式距离。

3.5 引入爆炸半径动态调整机制

引入爆炸半径的调整机制是为了提高烟花算法跳出局部收敛的能力以及全局搜索能力，由于爆炸半径是烟花算法中的一个关键算子，它严重影响着算法的性能，因此将爆炸半径作为主要改进的环节。基本烟花算法的半径是根据式（1）所得，由Aˆ限制其最大值，每一次迭代的每个烟花爆炸半径均为随机产生。为了加强算法局部搜索以及全局搜索能力，因此采取动态调整Aˆ的方式，从而达到控制全部烟花爆炸半径最大值的效果。

DER（Dynamic Explosion Radius）如算法1所示：

算法1计算n+1 代爆炸半径

1.Amax=ub-lb

2.ifYmin＜fmin:then

3.s=Amax*As

4.else:s=Amax*Ab

5.endif

6.ifs＜1:then

7.s=Amax

8.As=As-0.01

9.end if

其中，Amax为初始半径兼最大半径，Ymin是该次迭代的最优适应度值，fmin 为上次迭代的最优适应度值，As、Ab是常数，控制半径s的变化，*表示相乘。算法1的计算复杂度是O( 1) ，额外的计算开销并不大，通过这样一个自适应的半径，可以对搜索范围进行微调，使算法能够更加精细的局部搜索和更宽广的全局搜索。

图5给出了爆炸半径的变化示意图，根据算法1，初始半径由函数的上界和下界决定，从图中可以看出，半径随迭代次数的增加而曲线下降，即搜索范围逐渐下降，从而产生更多的火花进行局部搜索，由于前期搜索范围很大，因此不可避免地减慢了前期的收敛速度。相比烟花算法的固定半径，动态缩小半径能够提高算法求解的精度，当达到最小爆炸范围后，将现有半径重置为初始半径，动态增大半径用以跳出局部收敛，同时减小As，使得半径曲线获得更快的下降速度，避免算法收敛过慢，直至达到迭代次数。

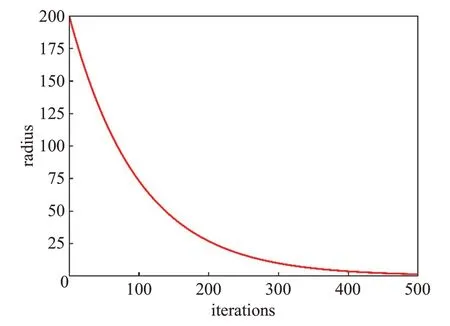
图5 爆炸半径曲线变化图

3.6 EFWA-DER流程

步骤1对N、dim、lb、ub、a、b、m、Aˆ、T等参数进行初始化，N为初始烟花个数，dim为目标函数的维度，lb、ub分别是函数搜索范围的上下界，a、b、m、Aˆ分别是给定的常数用来限制爆炸火花的半径和数量，T为函数评估次数。

步骤2根据式（1）～（3）计算t=1 时每个烟花产生的爆炸半径和火花数量，由式（4）和式（8）分别产生爆炸火花和变异火花。

步骤3如果产生的火花超出了搜索范围，则按照式（9）将其映射到可行域内。

滑窗宽度的取值与饱和度存在一定联系，图4为最优滑窗宽度与饱和点数的关系，当饱和点数小于初始窗宽W0时，最优窗宽在初始窗宽周围波动，当饱和点数大于W0时，最优窗宽与饱和点数大致成线性关系.

步骤4根据式（10）选择下一代烟花种群。

步骤5根据2.1 节的算法控制t=2 之后的爆炸半径变化，代入式（1）中。

步骤6循环步骤2～步骤5，直至达到最大函数评估次数。

引入动态爆炸半径算子之后，改进烟花算法爆炸半径能够根据上一代最优解自适应地改变，增加爆炸半径以提高全局搜索能力，或者减小半径以增强局部搜索，采用双精英的策略以保证个体的多样性，避免陷入局部最优。

3.7 算法时间复杂度对比

3.7.1 FWA时间复杂度

根据FWA流程，种群初始化的时间复杂度为O(N)，生成爆炸半径的时间复杂的为O(N)，产生火花的时间复杂度为O(N)，越界处理的时间复杂度为O(N)，计算欧式距离的时间复杂度为O(N×M)，轮盘赌法选择下一代种群的时间复杂度为O(N+N×M)，其中N是烟花种群数，M是烟花产生的火花数。所有步骤经过T次迭代，得到FWA时间复杂度如下：

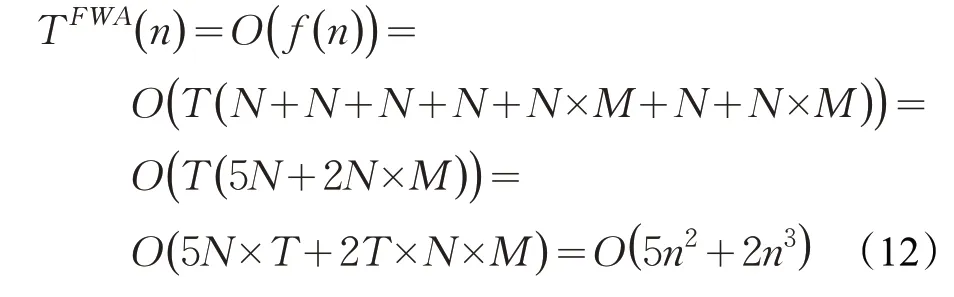
3.7.2 EFWA-DER时间复杂度

TFWA(n)-TEFWA-DER(n)=O(5n2+2n3)-O(6n2+n+n3)=O(n3-n2-n),因此EFWA-DER 的时间复杂度小于FWA的时间复杂度。

4 实验分析

4.1 实验设计

选择9 个包含单峰和多峰的标准测试函数，测试EFWA-DER 与FWA、SPSO2011 的寻优精度、收敛速度等性能。由于FWA 本身的缺点，对于原点和原点附近的最优值有较强的求解能力，所以增加了偏移函数的测试。文献[14]给出了EFWA 和FWA 的实验结果，EFWA在12 个标准测试函数上都表现出比FWA 差的性能，只在偏移函数的测试中性能更好，所以本文虽在改进的算子方面与EFWA 有所区别，但也不必将EFWA 加入比较。表1 给出9 个测试函数的表达式、搜索范围、最优点、最优值以及维度。

实验用Python实现，设置随机数种子确保各算法的随机数相同。FWA 和EFWA-DER 的参数设置如下：烟花N=5，爆炸数量参数m=50,a=0.04,b=0.8,爆炸半径参数Aˆ=40,As=0.99,Ab=1.01 ，SPSO2011 的参数设置参考文献[16]，偏移参数设置如表2 所示，SI 是偏移指数，SV 是偏移量。函数评估次数为1万次，设置20 个不同的 seed 值，运行 20 次，实验环境：Python3.7.3；Win10；Intel Corei5-8300H 2.3 GHz；8 GBRAM。

4.2 实验结果

4.2.1 标准测试函数结果

比较了3 种算法的在9 种函数上消耗的时间，FWA的运行时间为1，其余为FWA 的相对运行时间，由图6得出SPSO2011 的耗时最严重，在函数f1、f2、f5、f6、f8上EFWA-DER 小于FWA，而在f3、f4、f7、f9上则相反，EFWA-DER的平均耗时优于FWA。

表3 是测试函数在20 种不同随机数种子下运行取得的最优值和最差值，加粗数据为最优值。由表中数据可得，EFWA-DER、FWA在f3、f7、f9上均取得全局最优值，在f1上取得相同局部最优值。EFWA-DER 在f2、f4、f5、f8上的搜索结果相比FWA 有更高的求解精度，在f6上取得全局最优值。综合可得EFWA-DER的寻优结果要优于FWA。

表1 标准测试函数

表2 测试函数的偏移信息

图6 两种算法相对FWA的运行时间

图7 给出了9 个函数的收敛曲线，为了明显地观察各种算法的曲线变化，对9个函数选择各自适合的迭代次数，根据图7和表3得出，在f1、f3、f6、f8、f9上EFWADER 的收敛速度低于FWA，在f2、f4、f7上EFWA-DER与FWA的收敛速度相差不大。因此，在不排除FWA本身存在缺陷的情况下，EFWA-DER的收敛速度不如FWA。

综上所述，FWA-DER 的寻优时间和搜索结果均优于FWA，在收敛速度上不如FWA。

表3 不同随机数下各算法的寻优结果

4.2.2 偏移测试函数结果

9种测试函数中，算法仅在f3、f7、f8、f9上不受随机数影响并取得了最优值，所以只对它们进行偏移测试。表4给出了具体的实验数据，由于数据并不直观，图8显示了2 种算法偏移结果的折线图。由图8 可见，EFWADRE在偏移条件下的曲线更平稳，且偏移程度更小，因此FWA 易在原点或原点附近寻优的缺陷是显而易见的，EFWA-DER则不存在这样的问题。

图7 标准测试函数的收敛曲线

4.3 实验结果分析

4.3.1 基准测试函数实验结果分析

FWA 易于在原点或原点附近寻优，这是由于其映射规则和高斯变异均会将解映射和变异到原点附近导致的。从基准测试函数实验结果中可以看出，因为测试函数的最优点为原点或原点附近的值，所以FWA 的前期收敛速度很快，能够以较少的迭代次数搜索到原点或原点附近的解，但这并非是算法本身的智能产生的，同时随着迭代次数的增加，其跳出原点附近，即局部最优的能力并不足够强。相比之下，FWA-DER 通过改进算子解决了该问题，不易在原点或原点附近寻优，而是正常的智能寻优，由于动态调整了搜索范围，所以FWADER前期是在整个解空间进行大范围的全局搜索，随着迭代次数逐渐增加，搜索范围随之减小，FWA-DER的局部搜索能力逐渐加强，搜索精度因此提高。

4.3.2 偏移测试函数实验结果分析

在偏移实验下，FWA表现出了糟糕的结果，因为此时基准测试函数的最优点经过了偏移，不再处于原点或原点附近，其映射规则和高斯变异又不断产生原点附近的解，反而导致了算法的性能下降。FWA-DER 则不存在这方面的问题，相比FWA表现出更好的效果。

4.3.3 FWA与FWA-DER寻优能力分析

FWA的寻优范围是根据式（1）计算，搜索的上限为Aˆ，每个烟花产生一个相应的爆炸范围，较大的范围内产生少量火花作为全局搜索，较小的范围内产生大量火花作为局部搜索。FWA-DER 使得全局搜索的范围更大，局部搜索的范围更小，通过算法1 完成搜索范围曲线的动态调整从而提高全局寻优能力和局部寻优能力。

5 结论

基于烟花算法中存在的缺陷，本文结合增强烟花算法思想提出了一种带有动态爆炸半径算子的增强型烟花算法EFWA-DER。EFWA-DER 改进了基本算子，解决了烟花算法易于原点或原点附近寻优的缺陷，也使得算法耗时更少，同时动态爆炸半径算子加强算法跳出局部收敛的能力，提升算法搜索精度，整体上提高了算法优化性能。实验表明，本文提出的改进算法在前期收敛速度方面存在不足，有进一步提升的空间。

图8 函数偏移实验结果

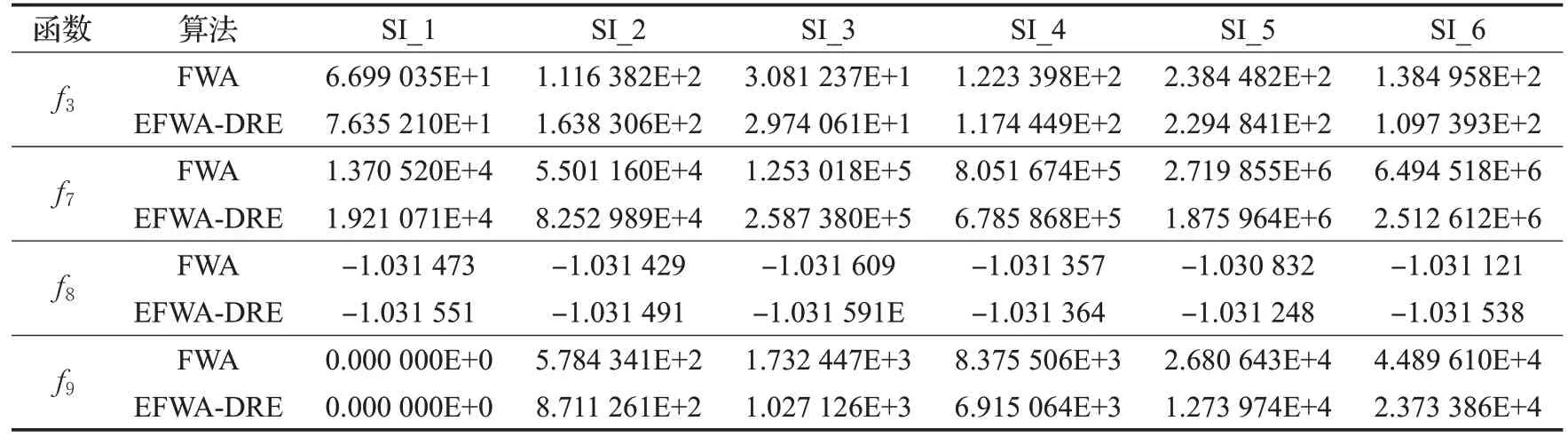
表4 不同偏移指数下的实验结果