路径规划的可定位性研究

高 扬，刘 江，李鹍鹏

长安大学 汽车学院，西安 710054

1 引言

路径规划结果的实现通常高度依赖于机器人准确的定位结果。已有对路径规划的研究中多集中于如何根据各种条件找到一条最优的路径，常用条件如：路径最短、时间最优、便于执行、能够避开障碍物等[1]。然而基于此类条件所规划出来的路径很少考虑到路径的可定位性，这使得机器人在跟踪路径的过程中很有可能因定位误差过大而导致路径追踪失败，因此在进行路径规划时将可定位性考虑进来具有重要的意义。本文主要研究常见的双轮差速机器人利用激光扫描仪，基于地图匹配与航迹推算的定位方法，建立了两者的定位误差方程，分别讨论了其可定位性对路径规划的影响[2]。

将定位的不确定性用分布的方差来描述在很多研究中都有被提到[3]。Roy最早在研究海岸线导航提出通过定位概率分布的熵值来反映机器人的可定位性[4]。Li等提出使用地图来辅助测量定位系统提供的信息可信度[5]。Censi等人基于Cramer-Rao定理从理论上给出了基于地图匹配定位的精度上限[6]。在Censi 等人的基础上又发展出来一系列研究机器人可定位性估计的研究成果。Qian 等人提出了一种引入动态障碍物影响因素的定位估计方法[2]。Wang 等人提出了一种基于可定位性的机器人动作选择机制，从而加速机器人全局定位的速度[7]。王炜等通过将概率栅格离散化，将Fisher 信息矩阵的应用扩展到概率栅格地图中去[8]。Wang 等人基于概率栅格地图和Cramer-Rao 边界的激光测距模型，将先验地图的不确定性考虑进来，加快了机器人的定位速度[9]。孙自飞等人利用离散化Fisher信息矩阵在线估计观测信息的可定位性矩阵，同时通过预测模型协方差矩阵评估里程计信息的可靠性，从而提高机器人的定位准确性和可靠性[10]。

近年来，也有不少研究是将机器人的可定位性考虑到路径规划中去。Censi 等通过计算期望激光数据以及激光扫描到的环境表面斜率，得到定位Fisher 信息矩阵，该矩阵可以反映可定位性的整体性和方向性，然而没有考虑地图信息的不确定性对可定位性评估的影响[11]。还有一些研究尝试使机器人在跟踪路径时位置不确定性最小，但是它们要求激光的扫描范围是360°，这就限制了其使用范围[12-15]。Irani等通过计算LM（Localizability Measure）来排除定位性差的区域，在此基础上再进行路径规划，可在一定程度上避免路径经过可定位性差的区域，但是需要通过阈值来调整通行区域，有可能因为阈值的设置过大而大幅扩大不可通行区域[16]。

已有研究中，可定位性是如何影响路径规划，并且如何去衡量路径的可定位性需要进一步地分析。因此，本文主要集中研究可定位性的影响并提出包含可定位性的新的路径评价函数。

2 可定位性对路径规划的影响

2.1 基于地图匹配和航迹推算的定位方差分析

机器人的定位结果一般来源于航迹推算和地图匹配两种定位方法的融合，这样可以获得更好的定位效果。设δm_s为基于地图匹配得到的定位估计方差，δd_s为航迹推算所得的定位估计方差，δf_s为融合后的定位估计方差。本文建立了δd_s的估计模型如式（1）和（2）所示：

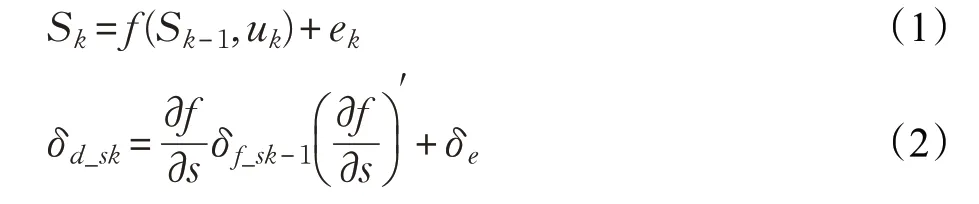
其中，f()为机器人运动方程，Sk(xk,yk,θk)为机器人当前时刻位姿，ek为机器人运动过程中所受到的噪声，假设ek服从均值为0，方差为δe的高斯分布。当忽略机器人中不准确的运动时，δd_s可以通过式（3）计算得到：

δm_s可依据文献[7]中方法由Fisher 信息矩阵求得其下限，如式（4）、（5）所示。riE为激光测距仪所得第i个激光束到障碍物的距离，δp为激光的白噪声。根据Cramer-Rao 理论，则可建立对δf_s的估计，即公式（5）。由于通常将航迹推算结果与基于地图匹配的定位结果融合使用。假设采用常用的卡尔曼滤波算法进行融合，则根据信息融合理论，δf_s可以根据公式（6）计算得到。

2.2 基于地图匹配和航迹推算的定位方差分析

δf_s代表融合定位后的方差，假设定位结果服从高斯分布，则其在概率分布上呈现为一个椭球的形状，椭球体积大小代表了机器人定位的不确定度。令δf_xy表示δf_s在X-Y平面的投影，它呈现为椭圆形状，代表机器人位姿估计在X-Y平面上的可能的分布范围。令δf_θ表示对机器人朝向角θ的估计。因此，δf_s可以表示为 (δf_xy,δf_θ)。如图1 中所示，令rs为障碍物的膨胀半径，ra为目标点的膨胀半径，R为机器人跟踪的路径，‖δf_D‖为δf_xy形成的椭圆度的长轴半径，三角形代表机器人的位姿，黑色方块代表障碍物，蓝色点为给定的路径的预瞄点，红色的点表示路径终点。

图1 定位不确定性的影响

2.3 δf_xy 和 δf_θ 对路径规划的影响

如图1中所示，假设机器人真实位姿落入该椭圆形包含的范围的概率不低于1-α，则该椭圆的长轴半径‖δf_D‖必然满足公式（7）：

在路径规划中，机器人应尽可能靠近障碍物以获得一条最短的路径。而‖δf_D‖越大，机器人撞到障碍物的可能性就越大，为了减少机器人碰撞的风险，‖δf_D‖应该满足式（8）。同时为了减少由于定位不确定性导致机器人不能到达目标点的风险，‖δf_D‖还应该满足式（9）。

对于角度误差δf_θ对路径规划带来的影响，本文分析了不同δf_θ条件下，机器人跟踪路径形成的轨迹长度L，如图2所示。

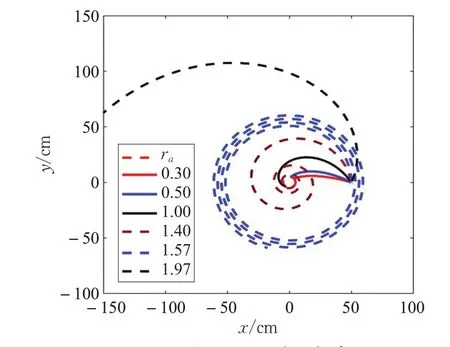
图2 不同的δf_θ 的路径长度

分析结果表明δf_θ与L间存在如式（10）的关系：

其中X0为机器人到目标点间的起始距离，而参数p1=-6.375 ；p2=3.766E+04 ；q1=-1.436E+04 ；q2=2.669E+04。

3 定位不确定性评价函数

在路径规划中通常借助评价函数将优化目标映射到一个有限的值域，采用不同的路径规划方法，所采用的评价函数形式也不一样。本文采用文献[15]中提出的基于粒子滤波的全局路径规划方法，因而采用sigmoid函数建立可定位影响评价函数，将 ‖δf_D‖和δf_θ对路径规划带来的影响映射到[0，1]。δf_s表示融合和后的定位方差，可由(δf_xy,δf_θ)表示，‖δf_D‖为δf_xy在X-Y平面投影上圆的直径，代表了δf_s在X-Y平面上定位方差的大小，‖δf_D‖和δf_θ值越小，代表着定位方差越小，机器人的定位越准确。

3.1 δf_θ 影响的评价函数

如图2所示，δf_θ对路径规划具有负面影响，所以采用的评价函数Eθ(δf_θ),如公式（11）所示：

Eθ(δf_θ)的值越小，对路径规划的影响更小。θu2是一个可变参数，由于当时，此时机器人到达不了终点，所以取参数k2表示评价函数值的变化速率，根据实际情况调整。其他参数本文取k2=14.1，θu2=2，因此Eθ(1)=0.5，Eθ(1.4)≈1。

3.2 ‖ δ f_D ‖影响的评价函数

由3.1 节分析可知 ‖δf_D‖对路径安全性呈负面影响，且需满足如式（8）、式（9）要求。故设计评价函数E(‖δf_D‖)如式（12）：

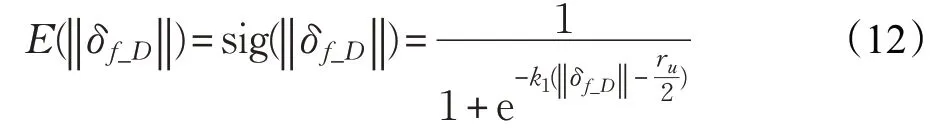
E(‖δf_D‖)的值越小，代表效果越好。其中由式（8）、（9）得到ru为由式（13）限制的最小值。

参数k1控制着评价函数值改变大小。图3 展示了它们之间的关系，其中k1分别取0.2，0.6，1，2，3，4。k1的取值要使得E(ru)≈1。故本文取k1=1，rs=50 cm ，rR=30 cm，ra=50 cm。

图3 在不同k 取值情况下E(‖ δ f _D ‖)和 ‖ δ f _D ‖的关系

3.3 基于可定位性的可定位性评价函数

在文献[17]中，采用了Ferguson 样条曲线来描述路径R，并提出评价函数E(R,MC)来平衡路径长度和机器人与障碍物之间的距离，E(R,MC)可由式（14）计算得知。结合本文所提出的可定性的评价函数，E(R,MC)可以扩展成新的评价函数Ep(R,MC)，如式（15）所示：

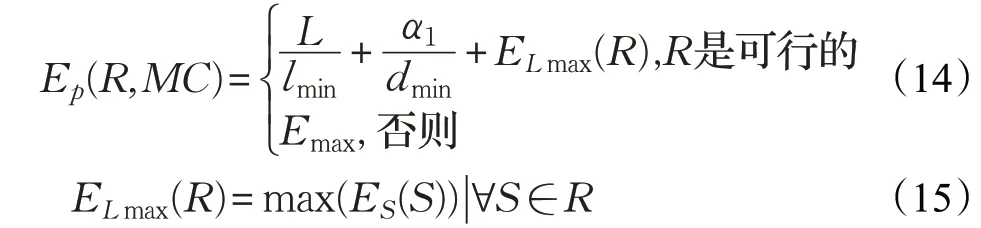
新的评价函数在路径规划的传统指标与可定位性指标之间做了平衡。式（14）中MC表示环境的地图，ELmax(R)是由式（16）求得的路径R的最大可定位评价值，ES(S)是给定路径点S的可定性评价值。L是由式（17）定义的路径R长度，lmin是起点P0到目标点Ta的最短距离。dmin为路径R到障碍物的最短距离，由式（18）求得，α1是一个权重系数。Xi(T)、Yi(T)为曲线i在X-Y平面的坐标，Xi′(T)、Yi′(T)为对T的导数。objx和objy为X-Y坐标系中距离原点最近的障碍物的坐标。α1,α2,α3是影响dmin,‖δf_D‖以及δf_θ的三个权重参数。

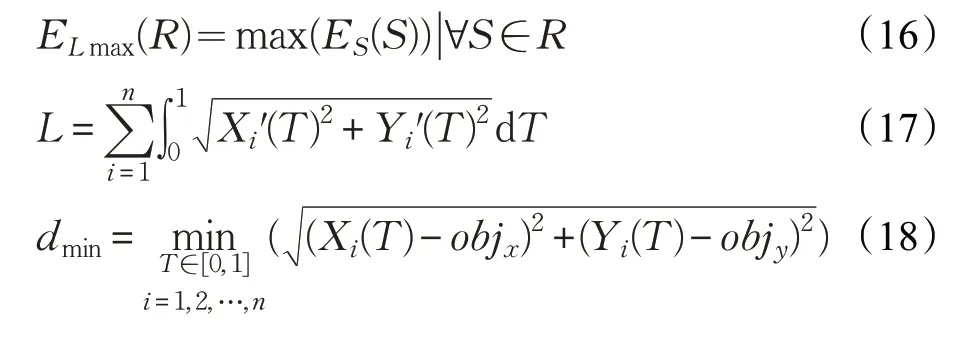
4 实验结果分析

为了验证本文所提出算法的效果，在图4（a）所示的室内环境进行了实验，图4（b）为实验所用概率栅格地图。实验机器人采用先锋机器人Pioneer 3-DX，如图5所示配置了里程计和激光测距仪（UTM-30LX）。控制器采用戴尔电脑，系统为Ubantu16.04，内存为8 GB。算法设置参数如下：激光扫描距离：Ld=3 m ，扫描范围[0°，270°]，激光束数目n=1 080 ，扫描周期T=25 ms。

图4 实验场地

图5 Pioneer 3-DX机器人

图6中红色的实线是传统的路径规划路线，蓝色的实线是加入了本文提出的路径评价函数生成的优化路径。在实验过程中机器人采用自适应粒子滤波定位的方法实现自定位，图6 中虚线代表机器人真实的轨迹。机器人在跟随传统路径时，由于穿行的区域定位误差过大，在实验过程中丢失了自己的位姿，不能成功地到达终点，而机器人在跟随本文改进后优化的路径，穿过的路径区域可定位性比较好，成功地到达终点。

图6 优化后的路径以及传统路径

图7展示了机器人在跟随优化后的路径时本文设计的四种可定位性评价指标(‖δf_D‖,δf_θ,E(‖δf_D‖),Eθ(δf_θ))的变化，‖δf_D‖其中代表δf_xy形成的椭圆度的长轴半径，δf_θ代表朝向角的方差，E(‖δf_D‖)代表 ‖δf_D‖的评价函数值，Eθ(δf_θ)代表δf_θ评价函数值。

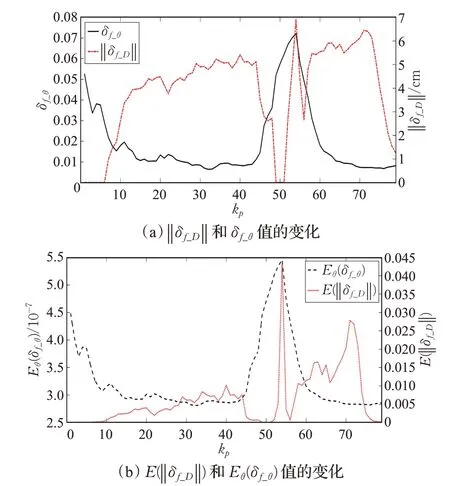
图7 优化路径的四种评价指标变化

图8 展示了机器人在跟随传统路径时四种评价指标的变化。可以明显看到在跟随优化后的路径时四种评价指标的值比较小，这使得机器人可以成功地到达目的地。相反机器人在跟随传统路径时，从第75 处定位到115处定位，由于δf_θ比较大，使得机器人由于定位误差比较大而不能达到终点。

5 结束语

本文主要研究定位不确定性对路径规划和路径跟踪的影响。通过将定位的不确定性分解为坐标定位方差和朝向角估计方差降低了可定位性评估难度。分析了两者对机器人路径跟踪的影响，在此基础上，提出了一个评价函数来评价不确定性对路径规划影响。实验表明，评价函数成功地描述了不确定性的影响，使得机器人在进行路径规划时可以在传统指标与可定位性指标间取得平衡。

图8 传统路径的四种评价指标变化