自适应遗传算法在机器人路径规划的应用

徐 力，刘云华，王启富

华中科技大学 机械科学与工程学院，武汉 430074

1 引言

随着智能制造技术的应用与推广，在港口及仓储等方面的自动化需求日益旺盛，AGV 机器人技术得到越来越广泛的应用。路径规划是AGV机器人技术的重要组成部分，研究高效可靠的路径规划算法，规划出AGV机器人从起始位置运动到目标位置的最优路径，对保障机器人工作稳定性，提高港口或仓库的运行效率起着至关重要的作用。

路径规划问题约束关系复杂，属于NP 困难问题。国内外针对AGV 机器人路径规划进行了大量的研究，主要的方法有几何法、随机采样方法、智能规划方法。几何法中主要包括可视图法[1]、栅格法[2]、轮廓法[3]、A*算法[4]、D*算法[5]、Dijkstra算法[6]等。随机采样方法主要包括概率路径图法和快速扩展随机树法等。智能规划方法主要包括BP 神经网络[7]、蚁群算法[8]、粒子群算法[9]、遗传算法[10]等。几何法需要对环境进行预处理，对于复杂的环境进行描述和计算较困难，较为适用于解决低维空间低自由度问题。随机采样方法作为增量式算法，是渐进最优的，收敛速度慢[11]。智能规划方法是建立在生物智能或者物理现象基础上的随机搜索算法，遗传算法是智能规划方法主要算法之一，相比于其他搜索算法而言，遗传算法在适应度函数对个体的评价下不断进化，使种群的适应度不断提高，进行有方向性的自适应搜索，适合求解路径规划问题。近年来部分学者基于遗传算法求解路径规划问题的研究取得了可喜的进展，田欣等[12]提出新的遗传参数自适应调整方式以提高自适应遗传算法的寻优效率；雷永锋等[13]提出正弦式自适应遗传算法以避免种群进化停滞和陷入局部最优等现象；胡赤兵等[14]提出遗传算子的自适应调整函数对遗传算法进行改进，提高算法效率及有效性。

AGV 机器人路径规划中需要处理复杂的避障问题，现有遗传算法在种群初始化、算法迭代等环节代价函数建模困难，路径搜索效率低[15]，耗费较大的计算和存储资源，尤其在求解复杂工程约束环境下的路径规划问题时效率低下，往往需要花费很长时间才能规划出可行路径，而且容易陷入局部最优问题[16]。针对这一问题，提出一种基于自适应遗传算法的机器人路径规划方法，该方法引入逆转算子，并添加插入算子和删除算子，提出新的自适应策略调整交叉和变异算子，有效降低陷入局部最优概率。

2 问题描述及空间建模

车间AGV机器人路径规划是在障碍空间中计算待规划机器人从初始位姿到最终位姿所经历的一系列点和线所组成的无干涉无碰撞轨迹，且轨迹为满足优化目标（如路径最短，转动角度最小等）的合理可行路径。在路径规划算法中，考虑到AGV机器人外形尺寸影响，需对障碍物的尺寸向外扩展，以便将机器人表示为搜索空间中质点，由轨迹规划算法计算出从起点到终点的一系列点和线所连成的轨迹路径。

机器人路径规划过程本质上是在满足约束条件的所有可行路径中搜寻一条最优路径或多条可行路径，该过程可表示为：

式中，f(p)为路径相关的目标函数，p为路径，ps为起点，pt为终点，Γ(ps,pt)为从ps至pt的路径集合。

为提高路径规划算法执行效率，通常需要进行路径规划空间建模。不妨以左下角为坐标原点，建立如图1所示的二维直角坐标系，设规划空间的像素坐标范围为(Xmin,Xmax,Ymin,Ymax),X、Y轴的像素单位为px、py,X、Y轴的等分数为nx,ny,则有：

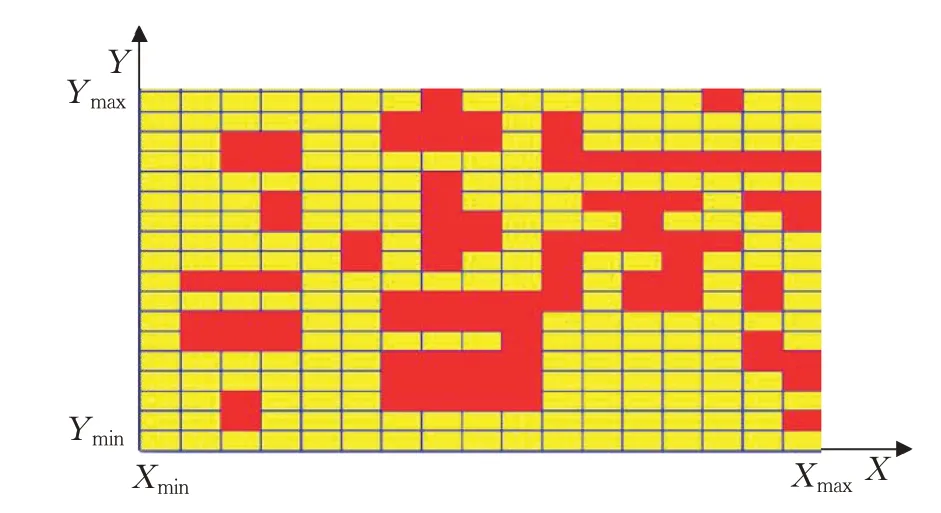
图1 路径规划空间建模

将图1规划空间划分为一系列栅格，每个栅格用点(xi,yi)表示，从原点起沿X、Y轴对栅格编号，编号为：

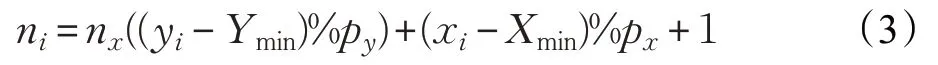
3 改进自适应遗传算法

3.1 生成初始种群

现有遗传算法求解路径规划问题时初始种群往往是随机选取，易产生不可行路径，影响规划算法求解。为避免引入不可行初始路径，需要利用机器人起止位置信息产生初始种群。其步骤为：将机器人初始位置作为起点加入路径，在起点所在行中的搜寻所有可行栅格并随机选取一点作为路径下一点，依此方法逐行搜索并确定一个可行栅格加入路径，直到终点所在行，并将机器人目标位置作为终点加入路径。该方法确保初始路径可行，避免了现有遗传算法随机产生初始种群可能导致初始路径不可行的问题，提高规划路径搜索效率。

3.2 适应度函数

通常遗传算法中采用适应度函数评价种群个体质量，用于确定该个体进入下一轮迭代的概率，对遗传算法的收敛速度以及找到最优解的概率起着至关重要的作用。适应度函数与路径距离相关，其路径总长为：

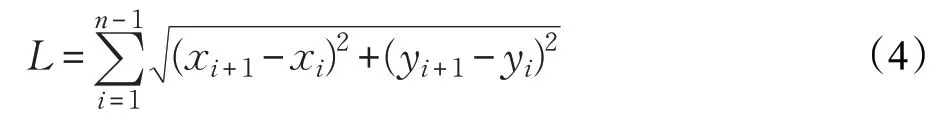
上式只考虑路径距离，未能考虑种群个体相邻两点间距离的影响，相邻两点距离较远易导致可行路径遗漏，需减少相邻两点距离较远的个体数目，增加种群搜索范围，为此在上式中增加路径途经栅格数目修正项，修正后的L′为：

式中n为该路径所通过的栅格数目总和。

为保证算法有效避障，采用路径相关的惩罚函数增大种群中路径包含障碍物较多个体的适应度，增加淘汰不良个体可能性。设pi、pi+1为相邻两个栅格点编号，pi pi+1表示相邻两点连线所涉及的栅格，f(pi pi+1)为pi pi+1中包含障碍物栅格的数量，则惩罚函数表示为：

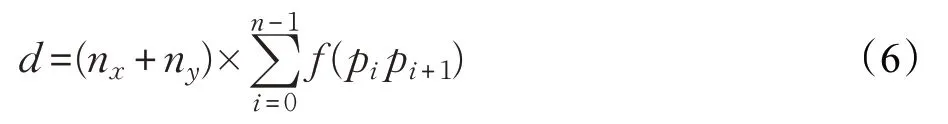
结合修正后路径长度和路径相关的惩罚函数，机器人路径规划的适应度函数表示如下：

3.3 改进遗传算子

现有遗传算法的基因操作通常有选择、交叉及变异等操作，但仅有以上操作难以有效避障，产生自交回路可能性高，易陷入局部最优等问题，导致难以搜寻可行路径，为此加入删除、插入和逆转等操作算子，具体实现如下：

（1）删除算子。路径中可能会出现自交回路，增加了不必要的搜索路径长度，浪费计算资源。通常自交回路在交点处存在相同的栅格编号，利用删除算子判断路径中是否存在重复栅格编号及自交回路，若存在则删除重复编号及自交回路。通过删除算子对种群进行操作有助于消除自交回路，缩短路径长度。

（2）插入算子。路径中部分相邻栅格可能存在距离较远，跨域不同邻域等问题，导致搜索路径容易遗漏。引入插入算子判断相邻栅格是否处于同一邻域，并将跨邻域相邻栅格的连线中点栅格编号插入路径，依此方法对所有跨邻域相邻栅格插值直至满足同一邻域定义要求。

（3）逆转算子。路径规划是复杂的迭代计算过程，其迭代求解过程中可能存在相邻迭代种群最优适应度偏差过小，导致求解结果陷入局部最优。在相邻迭代适应度偏差小于阈值时，引入逆转算子对全局种群中每个个体除起点和终点外随机确定两个节点，将路径中这两个节点间隔的其余节点全部删除并重新生成连续路径，若新生成路径适应度值更优则替换原先路径参与迭代计算。逆转算子较局部搜索的变异算子增强种群全局搜索及路径变化可能性，减少陷入局部最优的概率。

3.4 自适应策略

现有遗传算法中合理选择交叉概率pc和变异概率pm是影响算法收敛性及求解最优路径质量的关键因素。pc值过小，计算迭代过程中新个体难以产生，导致搜索过程缓慢，但过大的pc会破坏遗传模式。pm过小不容易产生新个体，种群不能得到更新，pm过大不利于保留优良个体，导致搜索缺乏导向性。

由于pc和pm对算法性能和收敛性的巨大影响，所以不能人为随意选取。为提高遗传算法的收敛速度和性能，引入自适应交叉概率p′c和自适应变异概率p′m替换pc和pm，具体表达为：

式（8）和式（9）分别用于计算种群内个体交叉及变异概率，式中pc1、pc2为初始设定的交叉概率的最大值和最小值，pm1、pm2为初始设定的变异概率的最大值和最小值，f′为进行交叉操作的两个个体间适应度的大者（简称为交叉个体适应度），favg为种群平均适应度，fmax为种群最大适应度，f为变异个体的适应度。按式（8）和式（9）计算的自适应交叉及变异概率随种群内个体适应度值变化规律如图2所示。

图2 自适应交叉及变异概率

图2（a）中交叉个体适应度f′接近平均适应度favg时其自适应交叉概率p′c较大，f′接近种群最大适应度fmax时p′c较小。图2（b）中变异个体适应度f接近favg时其自适应变异概率p′m较大，f接近fmax时p′m较小。

自适应遗传算法中采用自适应交叉概率p′c和自适应变异概率p′m进行交叉和变异操作，在路径规划迭代搜索前期阶段，种群个体间适应度分布较为分散，随迭代轮次增加，种群个体适应度分布逐渐趋于集中。种群个体间适应度分布对路径规划算法收敛性的影响分以下两种情况讨论。其一，算法迭代搜索前期，个体间适应度较为分散，自适应遗传算法的交叉和变异概率比现有遗传算法更小，保留种群内优良个体的概率更高。其二，迭代搜索后期，适应度越来越集中，自适应遗传算法具有更大的交叉和变异概率，在保留优良个体的条件下可提高加入新个体的概率，从而有效降低陷入局部最优的可能性。

3.5 改进自适应遗传算法实现步骤

基于现有遗传算法的选择、交叉、变异操作，改进自适应遗传算法通过加入删除、插入及逆转算子，采用自适应策略对交叉和变异操作进行调整，获得自适应交叉和变异概率，以此为基础进行路径迭代搜索，具体算法思路如下：

步骤1获取AGV 机器人起点和终点信息，设置算法参数。

步骤2采用3.1节所述算法生成初始种群。

步骤3计算当代交叉概率，执行交叉操作，产生新种群。

步骤4计算当代变异概率，执行变异操作，产生变异后种群。

步骤5将种群中个体代入适应度函数计算适应度值。

步骤6判断是否满足适应度偏差条件，若满足逆转条件，则执行逆转操作，若不满足转步骤7。

步骤7判断是否满足终止条件，若满足则输出结果，否则转步骤3，继续执行算法直至相邻迭代种群最优适应度偏差小于阈值或达到指定迭代次数。

算法流程图如图3所示。

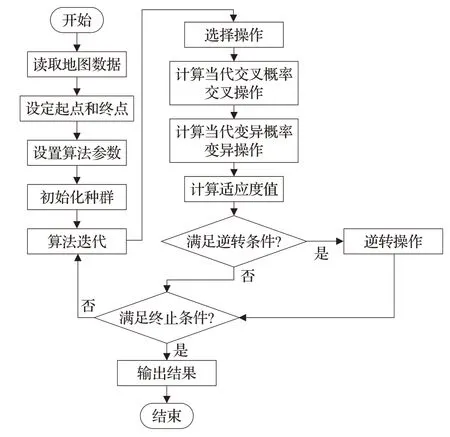
图3 自适应遗传算法流程图

4 算法验证

4.1 MATLAB算法验证

基于上述算法，基于MATLAB R2016a进行算法验证，分别使用传统遗传算法、文献[17]提出的改进遗传算法以及本文的改进自适应遗传算法进行算法对比分析及验证。三种算法验证参数设定为：种群大小为80，进化代数为200 代，选择概率为0.9，交叉概率为0.7，变异概率为0.01，改进自适应遗传算法交叉概率最大值为0.8，最小值为0.6，变异概率最大值为0.1，最小值为0.01。为消除随机性等偶然因素，在图4（a）所示的20×20栅格地图以及图4（b）所示40×40 栅格地图中分别重复运行三种算法100次。

使用传统遗传算法、改进遗传算法、改进自适应遗传算法对图4（a）算例进行避障路径规划，规划出的路径如图5所示，三种算法的适应度值与迭代次数关系对比如图6所示，在100次重复运算中所求解的最短距离、相邻迭代适应度偏差小于阈值的迭代代数及迭代收敛耗时作为评价指标。具体结果如表1所示。

表1显示，改进自适应遗传算法规划出的路径比传统遗传算法规划出的路径长度缩短了11.1%，比改进遗传算法规划出的路径长度缩短1.9%。改进自适应遗传算法以更少代数和更短时间规划出最优路径。

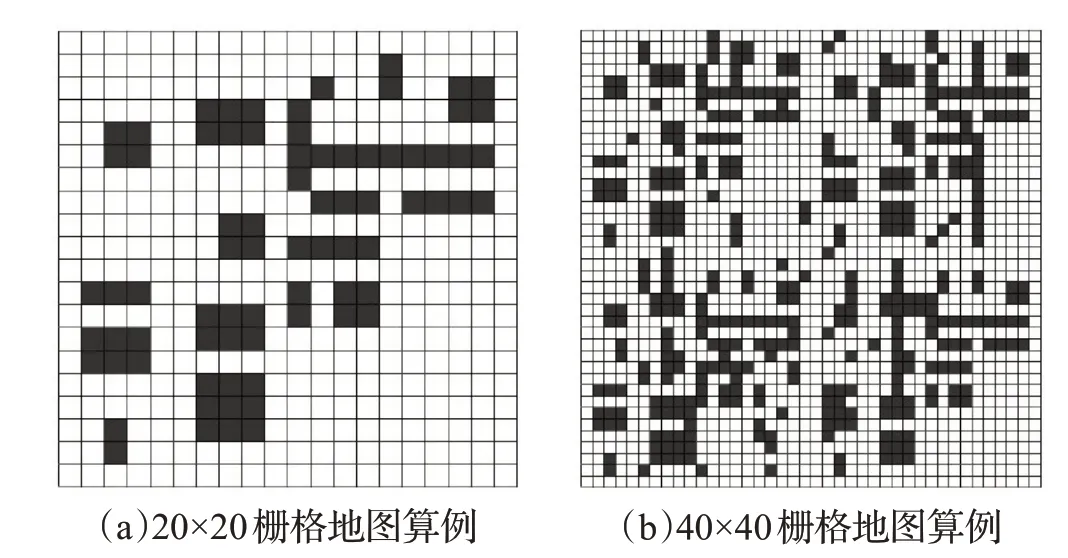
图4 栅格地图算例

图5 图4（a）算例规划路径对比

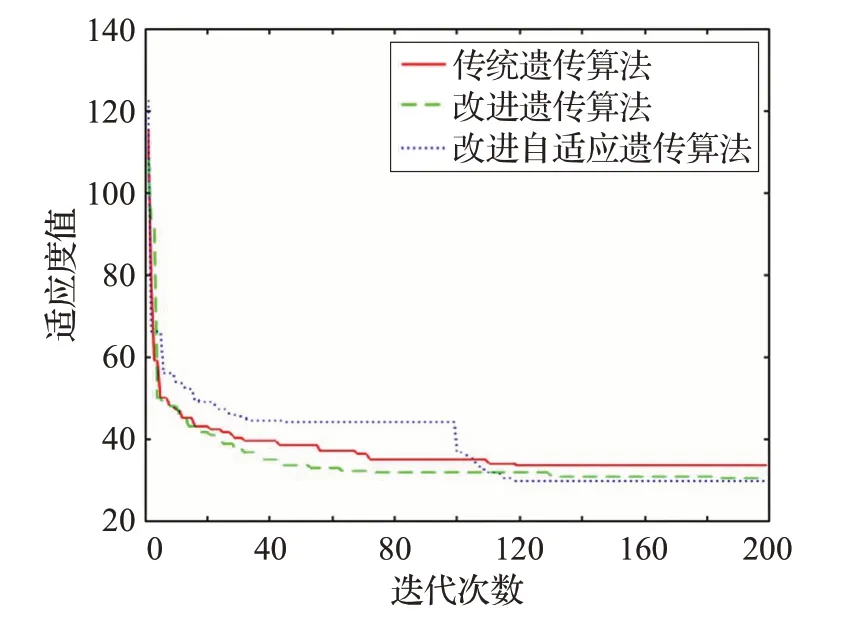
图6 图4（a）算例适应度值与迭代次数关系对比

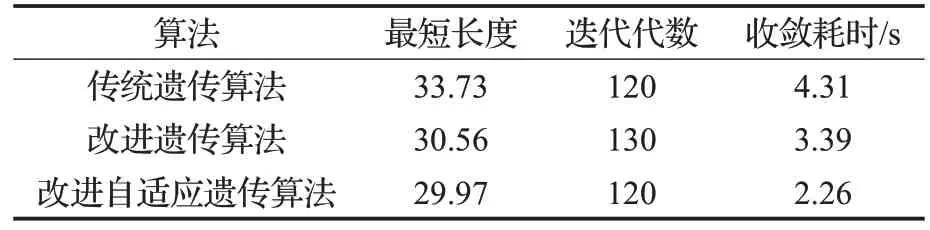
表1 图4（a）20×20栅格地图算例对比

图4（b）为40×40栅格地图算例，该算例障碍分布较为密集，其初始参数设置与图4（a）算例相同，规划出的路径如图7所示，三种算法的适应度值与迭代次数关系对比如图8所示，其计算结果如表2所示。

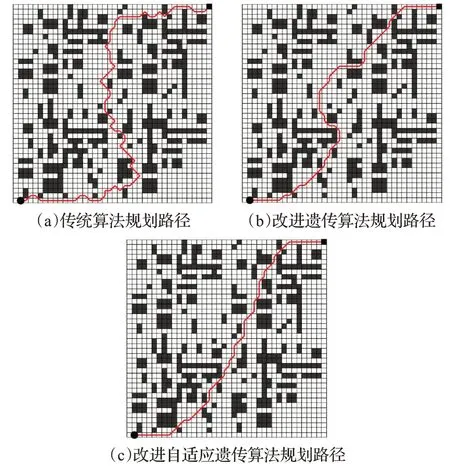
图7 图4（b）算例规划路径对比

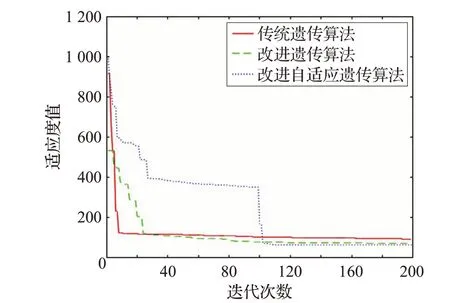
图8 图4（b）算例适应度值与迭代次数关系对比

表2 图4（b）40×40栅格地图算例对比

表2显示，在图4（b）算例中改进自适应遗传算法比传统遗传算法求解路径长度缩短31.7%，比改进遗传算法缩短9.4%。改进自适应遗传算法在更少迭代代数能找到更优路径。

上述验证算例表明，改进自适应遗传算法能以更少的迭代次数、更快的收敛速度得到更优路径，且能有效避免陷入局部最优。

4.2 系统应用验证

基于上述算法，采用面向对象的开发语言VC++11，研究开发了面向制造车间装配工艺仿真的AGV机器人路径规划软件模块，该模块在华中科技大学CAD 中心自主研发的三维工艺规划与仿真系统——Inte3D 中得到应用，如图9所示。在Inte3D系统中采用改进自适应遗传算法对环境中的AGV 机器人进行路径规划，最终生成机器人的无碰撞运动轨迹，并用动画仿真形式直观展示AGV机器人在车间中运动场景。

图9 Inte3D中AGV机器人路径规划软件模块

Inte3D 系统中对于机器人所在空间进行环境建模及栅格编码，计算障碍物信息，给定AGV机器人的起止栅格编号，设定改进自适应遗传算法初始参数，调用路径规划算法进行计算，图10为在某制造车间AGV路径规划实例。

图10 规划路径

该实例中制造车间共划分为1 600 个栅格，单个栅格长为1 400，宽为700，计算出的最优路径为65.36，耗时4.5 s，实例表明改进自适应遗传算法能以较快的速度规划出较短路径。

5 结束语

针对现有遗传算法求解路径规划问题时存在的收敛速度慢、易陷入局部最优等缺点，提出一种基于自适应遗传算法的机器人路径规划方法。该方法引入逆转算子，增加插入算子和删除算子，采用自适应策略对交叉和变异概率进行调整，有效提高收敛速度，降低陷入局部最优可能性。算法分别在MATLAB和Inte3D系统中进行算例验证，结果表明改进自适应遗传算法相比传统遗传算法以及改进遗传算法更为有效。考虑到实际工程中生产车间设备布局较为固定，通常AGV 机器人运动轨迹规划是在工艺路线规划仿真环节中完成，并利用数字孪生技术对仿真路径与实际物理路径进行对比分析，实现对AGV 机器人的调度监控。工程应用验证表明改进自适应遗传算法能满足车间AGV机器人规划仿真需求。