抗蛇形减振器外特性建模仿真及试验研究

刘 秋，孙晋伟，顾 亮

（北京理工大学机械与车辆学院，北京100081）

1 引言

为了使轨道车辆具有转向能力，其轮毂踏面形状通常为锥形，这也意味着其在直线行驶的过程中会出现蛇形运动，只不过对于低速的轨道车辆（往往以160km/h 为界），蛇形运动对列车的行驶稳定性与安全性影响较小[2]。但是对于高速列车，当其以较高的速度行驶时，微小的横向振幅最终都有可能造成剧烈的蛇形运动，使得轮缘不断地撞击钢轨，加速轮轨以及车轮的磨损，极大地破坏了高速列车的行驶稳定性与安全性。抗蛇形减振器的主要作用就是抑制高铁在高速行驶过程中的蛇形运动以保证高铁的行驶稳定性与安全性。

目前，抗蛇形减振器的主要形式为双筒式液压减振器。国内外已有许多学者对双筒式液压减振器的建模以及阀片变形计算进行了研究，例如文献[4]利用弹性力学原理推导了减振器阀片受均布压力时变形量计算的解析公式，文献[6]则是给出了阀片受线性非均布压力时变形量计算的解析公式，文献[7]基于上述解析公式对减振器进行了建模仿真，并分析了减振器结构参数对外特性的影响规律。但是上述工作均以减振器节流阀片的整个环形面受均布或线性非均布压力为前提，对于大部分的减振器来说，其阀片的受力往往不是整个环形面受力，受压面也不一定与活塞杆的轴线对称，仅利用弹性力学原理难以得到阀片变形量的解析公式。因此将有限单元法与弹性力学原理相结合，通过matlab 编程计算节流阀片变形，保证了阀片在复杂受力情况下变形量计算的精度，最后结合减振器液压数学模型，建立了完整的减振器外特性仿真模型，并通过相应的试验验证了其正确性。

2 减振器建模与速度特性分析

以抗蛇形减振器的实际结构为基础，基于液压流体力学的相关理论，以复原过程为例阐述了建模过程，分析了油液的通流油路以及各油路之间的串并联关系，并给出了相应的数学表达式。

减振器建模的主要工作就是根据实际结构推导出各节流处流量与压差的关系，然后再分析出各节流处油路串联与并联的关系，最后列出整个复原过程或者压缩过程流量与压差的关系，从而得到相应于某个速度下减振器的阻尼力。在建模过程中忽略油液和减振器内缸筒的弹性特性、假设减振器任何一个腔室中的压力在整个腔室内处处相等、忽略油液在各处的泄露。

2.1 复原阀开阀前油液流动分析

当减振器两端相对速度较低时，复原阀片两端的压差较低，还不足以使得节流阀片打开，此时油液只流经复原阀上的常通孔，常通孔的结构为两个不同半径的圆孔串联。此时常通孔的节流损失主要来源于局部损失，包括油液从复原腔进入常通孔大孔的入口损失、从大孔收缩到小孔的损失、收缩流在小孔中扩展开来的损失、从小孔流入压缩腔的出口损失[8]。然后根据液压流体力学中有关薄壁阻尼孔出流的理论，将上述各部分局部阻力损失均折算到小孔速度处可以得到：

式中：Q1—未考虑沿程损失时流经常通孔的流量；S1—小孔的面积；ΔP—活塞两端的压差；ρ—油液的密度；K1—上述各部分总的局部阻力损失系数（折算至小孔速度处）。

然后考虑大孔处的沿程损失，大孔段流速v1与雷诺数Re1分别为：

式中：d1—大孔的直径；υ—油液的运动粘度；S2—大孔的面积。

根据雷诺数判断此时油液在大孔处的流动状态，取下临近雷诺数为2000，若流动状态为层流，此时流动的阻力与管壁的绝对粗糙度无关。在液压技术中，考虑其它的影响后常采用下式计算相应的沿程损失系数：

若为湍流，常采用实际管道紊流过渡区公式计算沿程损失系数λ1为：

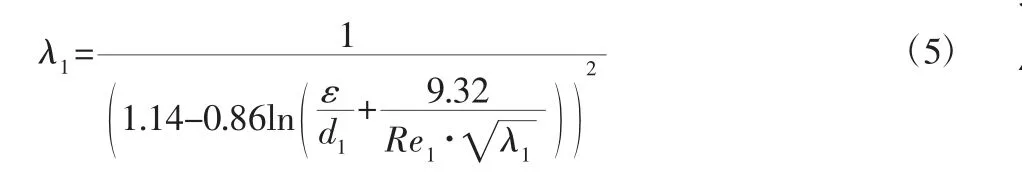
式中：ε—壁面的绝对粗糙度。

然后将大孔处的沿程损失折算为小孔处的局部阻力损失系数K2为：

式中：l—大孔的长度。

则通过常通孔的总流量为：

式中：K3—考虑沿程损失后总的局部阻力损失系数；K3=K1+K2。

此时减振器的复原阻尼力与减振器两端的相对速度分别为：

式中：P—活塞两端的压差；Sr—活塞杆与活塞缸之间的环形面积；f1—活塞与缸壁之间的静摩擦力。

2.2 复原阀开阀后油液流动分析

随着减振器两端相对速度的增加，复原阀节流阀片两端的压差增大从而使得阀片打开，此时油液既流经常通孔又流经复原阀，复原阀与常通孔共同节流，此时两者的油路为并联关系，复原阀结构，如图1 所示。

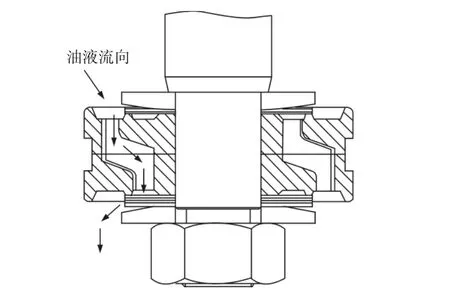
图1 复原阀结构图Fig.1 Structure of Recovery Valve

同理，将从阀通道入口处至阀片通流缝隙处的各项局部损失与沿程损失均折算至阀通道出口速度处的局部阻力损失，具体方法与上述常通孔的建模类似，只是各节流处的局部阻力损失系数有差异[8]。最后得到总的等效局部阻力损失系数为K4，则此时阀通道出口处的流速v3为：

阀片开度所形成的通流缝隙处的流速v4及其相应的雷诺数Re2为：

式中：d2—环形通流缝隙的当量直径；S3—阀通道出口处的面积。

根据雷诺数判断此时油液在阀片通流缝隙处的流动状态，取下临近雷诺数为2000，若流动状态为层流，则沿程损失系数为λ2：

若为湍流：

再将阀片通流缝隙处的沿程损失折算至阀通道出口速度处的局部阻力损失，相应的等效局部阻力损失系数为K5：

式中：l3—阀片通流缝隙的长度。

则复原阀总的局部阻力系数K6为：K6＝K4+K5

所以流经复原阀的总流量为Q3：

考虑流经常通孔处的流量Q2（根据前文的推导）可得总流量为Q4＝Q2+Q3。此时减振器的复原阻尼力Fr2与减振器两端的相对速度v5分别为：Fr2=P·Sr+f2（17）

式中：P—活塞两端的压差；Sr—活塞杆与活塞缸之间的环形面积；f2—活塞与缸壁之间的静摩擦力。

3 阀片变形量计算分析

针对阀片变形量的计算，给出了利用有限单元法与弹性力学原理分析该问题的过程与方法。

3.1 阀片单元特性分析

选用包含曲边的八结点Hencky 板单元来对节流阀片进行结构离散化，其示意图，如图2 所示。

图2 八结点Hencky 板单元示意图Fig.2 Schematic of Hencky Board Unit with Eight Nodes

根据弹性力学中的Hencky 薄板理论，对于边厚度、中面为平面曲边四边形的八结点板单元，其中面形状和厚度，如式（19）所示[9]：

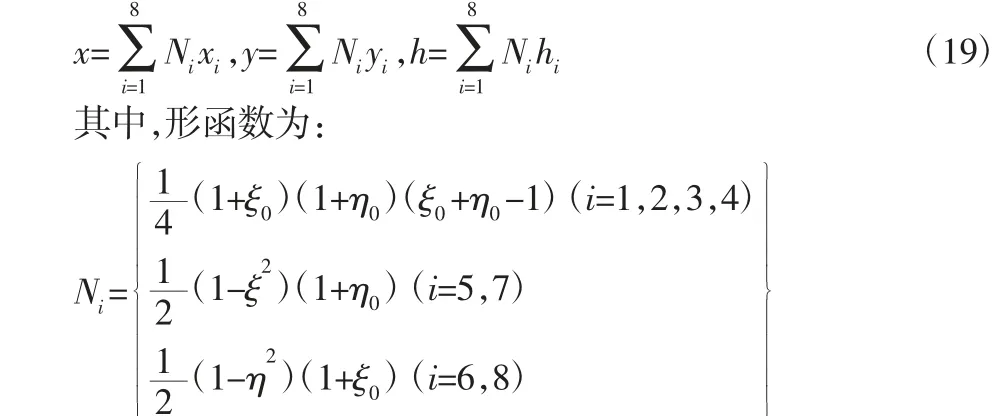
其中，ξ0=ξξi，η0=ηηi在下面的分析中，除了形函数以外，还需要形函数对子单元整体坐标（x，y）的一阶偏导数。

由于单元位移场是在局部坐标系（ξ，η）下描述的，而以位移求应变所用的公式是以整体坐标（x，y）表达的，要将形函数利用坐标变换式写成整体坐标（x，y）的显示表达一般是十分困难甚至是不可能的。因此利用复合函数求导法则将对直角坐标的求导运算变换成对斜角坐标的求导运算：

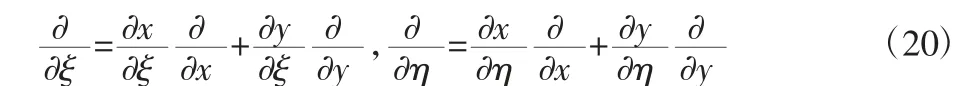
通过变换可得：

八结点Hencky 板单元的单元刚度矩阵ke可以写成分块形式，其中子块矩阵kij为：

式中：h—节流阀片厚度；E—阀片材料的弹性模量；υ—泊松比。

对于式（22）的积分，由于其显示的表达式十分复杂，积分起来十分的困难，因此采用二维高斯积分进行数值计算。

此外，在分布载荷q（x，y）（即为阀片所受到的压力）作用下单元的等效结点荷载矩阵为：

3.2 阀片变形量求解

利用前文中的有关内容计算出每个阀片单元的单元特性，基于每个阀片单元特性的分析结果，对于各单元仅在结点相互连接的单元集合体，利用虚位移原理或最小势能原理建立起表示所有结点平衡的整体刚度方程，如式（24）所示。

式中：K—阀片整体刚度矩阵；Pd—直接结点荷载；PE—等效结点

荷载；Δ—阀片结点位移矩阵。

整体刚度方程（24）通常是一组高阶的线性代数方程组。所以在解方程组时要利用整体刚度矩阵带状、稀疏和对称的特性提高计算效率。利用相应的计算方法，即可求出全部未知的结点位移，也就可以得到节流阀片在一定受力情况下任意一点处的变形。

4 仿真分析与试验验证

4.1 仿真分析

仿真程序基于Matlab 软件采用压差增量迭代法，首先根据抗蛇形减振器的实际结构确定相关的结构参数并选取一个初始迭代压力作为活塞两端的压差，然后根据所建立的数学模型以及有限元计算程序得到相应的阻尼力、减振器两端的相对速度以及此时的位移，并以相对速度作为迭代过程是否终止的判断条件，复原过程的仿真分析流程，如图3 所示。

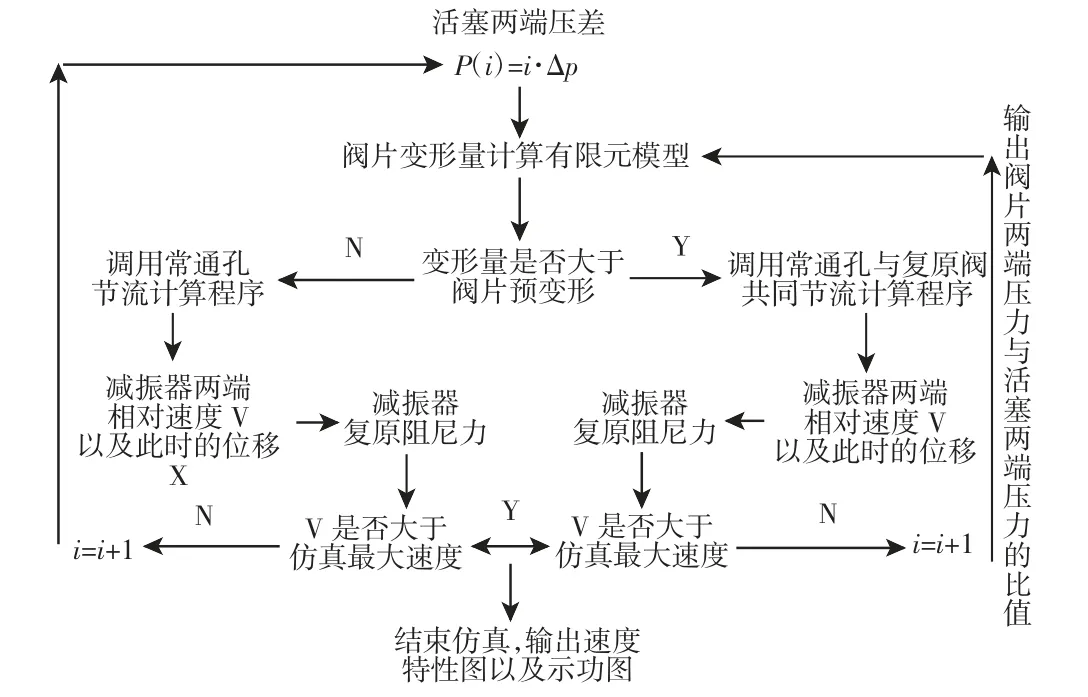
图3 复原过程仿真分析流程图Fig.3 Flow Chart of Simulation Analysis of Recovery Process

针对该流程，需要特别说明的是：当复原阀系还未开阀时，活塞两端的压差即为复原阀片两端的压差，而开阀后，两者不再相等，所以此时应计算出活塞两端压差与复原阀片两端压差的比值，然后输入至阀片变形量计算有限元程序中，这样才能准确计算出阀片的实际变形量。

4.2 试验验证

试验设备分别为MTS850 液压激振台及其相应的数据采集系统。振幅选择25mm，最大速度分别为0.1m/s、0.5m/s，根据简谐运动方程可知其对应的激振频率分别为0.64Hz、3.18Hz。减振器台架试验，如图4 所示。减振器示功图，如图5 所示。从图5 中可以看出，仿真的曲线与试验曲线基本吻合，证明了所建立的模型以及有限元计算的正确性。由于建模过程中没有考虑油液的可压缩性、活塞与缸筒缝隙处的泄露以及减振器的滞回特性，所以仿真曲线图是关于纵轴对称的一条光滑曲线。

图4 减振器台架试验图Fig.4 Shock Absorber Bench Test Chart

图6 减振器速度特性曲线图Fig.6 Shock Absorber Speed Characteristic Curve

从图6 可以看出，由于没有考虑减振器的滞回特性，所以仿真的速度特性曲线为一条开放的曲线而不是闭合的曲线，但是曲线走势、特定点的数值与试验结果基本一致。同样证明了所建立的数学模型以及有限元计算是准确合理的。

5 结论

针对节流阀片变形量在复杂受力情况下难以准确计算的问题，提出了有限单元法与弹性力学原理相结合的方法，然后根据抗蛇形减振器的实际结构，基于液压流体力学的相关理论，建立了减振器的数学模型，并将其与有限元计算程序结合进行仿真，仿真及试验结果表明：（1）基于抗蛇形减振器实际结构并结合液压流体力学建立的减振器数学模型与实际情况是相符合的，通过有限单元法与弹性力学相结合的方法对阀片变形量进行计算也是准确合理的。（2）是否考虑减振器滞回特性、活塞与缸筒缝隙处的泄露以及油液的可压缩性会影响减振器建模的精度。