基于C语言模拟计算的cdPCR最佳反应通孔数分析

周德良

（北京旌准医疗科技有限公司，北京 100190）

C语言是面向过程的高级程序设计语言[1-6]，具有功能强大、应用面广、使用简单方便、可移植性好等优点[2-4]。C语言不仅可以用于系统软件编写、单片机系统开发，还可以用于大数据统计与分析[3-4，7-8]。数字PCR（dgital PCR，dPCR）是一种核酸分子绝对定量技术[9-12]，其不需要采用看家基因或标准曲线，具有高灵敏度、高准确性、高耐受性、绝对定量等优点[13-16，22]。dPCR主要包括液滴数字PCR（ddPCR）和芯片数字PCR（cdPCR）两种，其中cdPCR通过把反应液均匀分到芯片上的反应通孔中进行PCR反应，然后根据泊松分布和荧光信号阳性比例来计算目的核酸的拷贝数[13]。

利用C语言程序来模拟芯片数字PCR中目的核酸进入反应通孔的过程，从而可以对干扰粒子对目的核酸分布的影响[17-20]、目的核酸最佳反应通孔数、目的核酸分布均匀性等问题进行分析与计算，旨在为数字PCR的芯片设计提供一定的参数依据与理论指导。

1 模拟分析算法

通过C语言模拟“干扰作用完全随机的情况下目标粒子进入反应通孔的过程”的模拟算法如图1所示，具体过程如下：

（1）在[0，h+n*h/m）区间内生成m+n个随机数，其中[0，h-1]区间内的随机数代表目标粒子，总数为m；[h，h+n*h/m）区间内的随机数代表干扰粒子，总数为n；h代表反应通孔数；

（2）统计[0，h-1]内非重复随机数的总数N，N表示m个目标粒子在h个反应通孔中的入孔总数；

（3）将上述过程重复K次，并统计不同N对应的出现次数Y；

（4）根据不同h对应的N-Y曲线的重叠度或N-Y主峰N值随h的变化率来判断最佳反应通孔数。

2 无干扰的最佳反应通孔数

在没有干扰粒子的情况下（n=0），为了分析目的核酸（或目标粒子）在检测芯片反应通孔内的分布情况，根据图1所示采用如下统计过程：

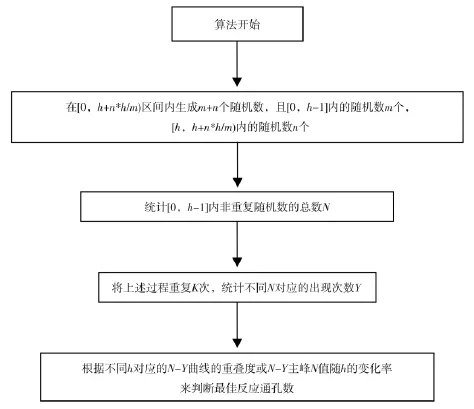
图1 模拟算法程序图Fig.1 The program graph of simulation algorithm

设目标粒子个数m为1 000，反应通孔个数h为1 000 a（a取1到10的所有整数）。当反应通孔数为1 000时（a=1），利用C算法程序随机生成1 000个介于[0，999]的随机数，代表1 000个目标粒子。当生成随机数x（0≤x≤999）时表示目标粒子落入标号为x的反应通孔内，统计1 000个随机数的非重复数值的总数N，N就表示1 000个目标粒子在1 000个反应通孔中的入洞总数。将上述过程重复20万次，统计不同入洞总数N对应的出现次数Y，从而得到1 000个目标粒子在1 000个反应通孔中的分布情况，如图2所示，其入洞总数非零区间为[589，674]，其中当入洞总数N=632时出现次数最大。

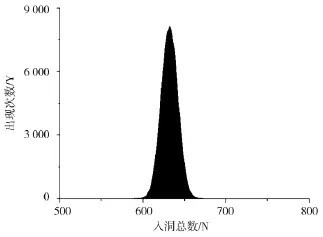
图2 1 000个目标粒子在1 000个反应通孔中的分布Fig.2 The distribution of 1 000 target particles in 1 000 reaction holes

当反应通孔数为2 000时（a=2），利用C算法程序随机生成1 000个介于[0，1 999]的随机数，当生成随机数x（0≤x≤999）时表示目标粒子落入标号为x的反应通孔内，并统计1 000个随机数的非重复数值的总数N。将上述过程重复20万次，统计不同入洞总数N对应的出现次数Y，从而得到1 000个目标粒子在2 000个反应通孔中的分布情况，如图3所示，其入洞总数非零区间为[745，829]，其中当入洞总数N=787时出现次数最大。

依此类推，可以得到当反应通孔数为1 000 a时（a分别为3到10的整数）1 000个目标粒子的分布情况，见图4。

对应图4，各曲线波峰对应的入洞总数N见表1，而由表1得到的曲线点图见图5。

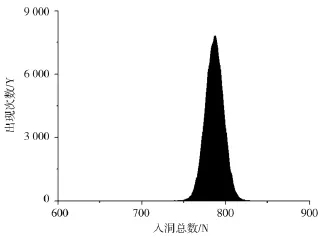
图3 1 000个目标粒子在2 000个反应通孔中的分布Fig.3 The distribution of 1 000 target particles in 2 000 reaction holes

图4 1 000个目标粒子在1 000 a（a为从1到10的全部整数）个反应通孔中的分布Fig.4 The distribution of 1 000 target particles in 1 000 a（a is integer from 1 to 10）reaction holes

表1 N-Y曲线波峰对应的入洞总数NTable 1 The value N corresponding to peak of curve

从图4发现，随着芯片反应通孔数的增多，1 000个目标粒子的入洞总数N也越来越大，即1 000个目标粒子的分布均匀度越来越高，但随着反应通孔数的进一步增多，不同反应通孔数对应的N-Y曲线的毗邻程度越来越高，重叠程度也越来越大；而表1和图5同样表明，虽然随着反应通孔数的增加目标粒子的分布均匀度会越来越高，但当反应通孔数大于某一值时分布均匀度的提高已开始趋于饱和（增加非常平缓）。因此，为提高目标粒子在反应通孔中的分布均匀度，直接有效的方法是增加芯片上的反应通孔数，但当芯片反应通孔数大于等于8 000或9 000时反应通孔数增加对提高目标粒子分布均匀度的作用将趋于饱和，如果继续增加反应通孔数，则将带来工艺难度的提升与设计成本的增加，特对是对于目的核酸片段较少、检测灵敏度要求不高的实验，高昂PCR仪显然与实际需求相违背。所以，在1 000个目标粒子的基础上，cdPCR检测芯片的最佳反应通孔数应为8 000或9 000，并由此推断，在无干扰粒子的情况下，不论目标粒子个数m取多少，检测目标粒子的最佳反应通孔数与目标粒子个数之比应为 8∶1 或 9∶1。

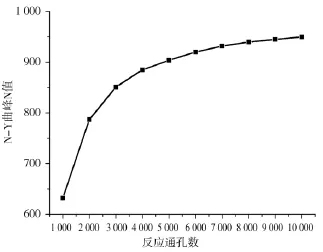
图5 表1数据对应的点线图Fig.5 The dot-line graph corresponding to the datum of table 1

3 含干扰的最佳反应通孔数

3.1 干扰粒子对目标粒子分布的影响

文献[21]分析了干扰作用完全随机的情况下，干扰粒子有无及其多少对目标粒子分布的影响，并得到了1 000个目标粒子在1 000 b个（b分别取0、10、100、1 000、10 000） 干扰粒子作用下分别在 1 000、3 000、7 000个反应通孔中的分布情况[21]，分别见图6、图 7与图 8，其中图 6～图8的（a）表示无干扰粒子对应的目标粒子分布；图 6～图 8 的（b）、（c）、（d）、（e）分别对应干扰粒子个数是目标粒子的10、100、1 000、10 000 倍的目标粒子分布；图 6～图 8 的（e）为前述5类情况的合成图。文献[21]得到结论如下：

不论反应通孔数h取多少，含干扰粒子与不含干扰粒子的5类N-Y曲线分布基本重合或相同，且干扰粒子个数越小，含干扰粒子的N-Y曲线分布与不含干扰粒子的N-Y曲线分布就具有越高的重合度或相似度。上述结果表明，在干扰作用完全随机的情况下，对于任意取值的反应通孔数h，干扰粒子有无及其多少均不会破坏目标粒子的随机分布程度，因此，无论有无干扰粒子或其存在多少，目标粒子的N-Y曲线分布都基本相同。

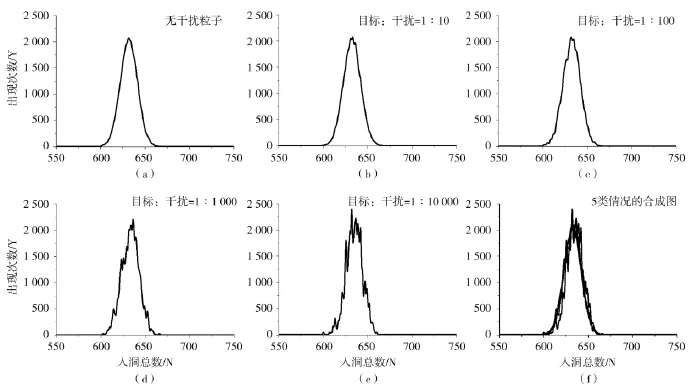
图6 目标粒子在1 000个反应通孔中的分布Fig.6 The distribution of target particles in 1 000 reaction holes

3.2 分析结果

分析表明，在干扰作用完全随机的情况下，对于任意取值的反应通孔数h，干扰粒子有无或其多少均不会破坏目标粒子的随机分布程度，因此，无论有无干扰粒子或其存在多少，目标粒子的N-Y曲线分布[21]都将基本相同。因此，“含干扰的最佳反应通孔数”与“无干扰的最佳反应通孔数”应该几乎一致，故仍可将含干扰粒子的最佳反应通孔数定为8 000或9 000（目标粒子个数为1 000的情况下），并由此推断，在含干扰粒子的情况下，不论目标粒子个数m取多少，检测目标粒子的最佳反应通孔数与目标粒子个数之比仍为 8∶1 或 9∶1。

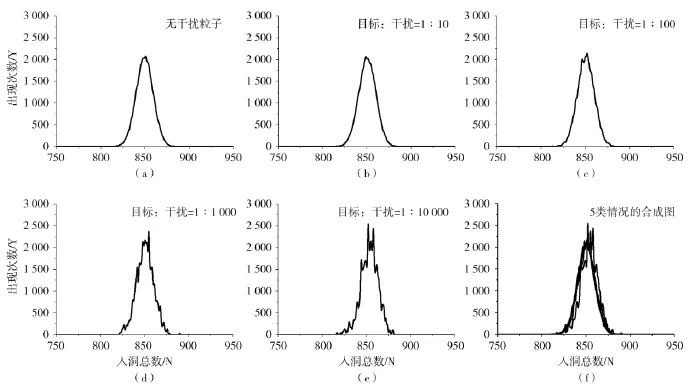
图7 目标粒子在3 000个反应通孔中的分布Fig.7 The distribution of target particles in 3 000 reaction holes

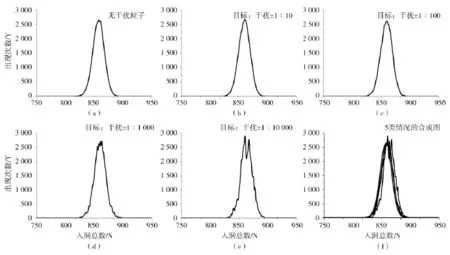
图8 目标粒子在7 000个反应通孔中的分布Fig.8 The distribution of target particles in 7 000 reaction holes

4 目标粒子分布的均匀性

目标粒子分布的均匀性定义为“含目标粒子的反应通孔数”与“目标粒子总数”的百分比。为了分析目标粒子在不同反应通孔数下的分布均匀性，采用如下统计方法：

设目标粒子个数为1 000，反应通孔数h为1 000 a（a取1到200的任一整数）。利用C算法程序随机生成1 000个介于[0，1 000 a-1]的随机数，代表1 000个目标粒子。当生成随机数x（0≤x≤1 000 a-1）时表示目标粒子落入标号为x的反应通孔内，统计1 000个随机数的非重复数值的总数N，N就表示1 000个目标粒子在1 000 a个反应通孔中的入洞总数。将上述模拟过程重复5万次，并计算入洞总数N的平均值，该平均值即“含目标粒子的反应通孔数”，再用其除以“目标粒子总数”，从而得到1 000个目标粒子在1 000 a个反应通孔中的分布均匀性，具体模拟计算结果见表2。

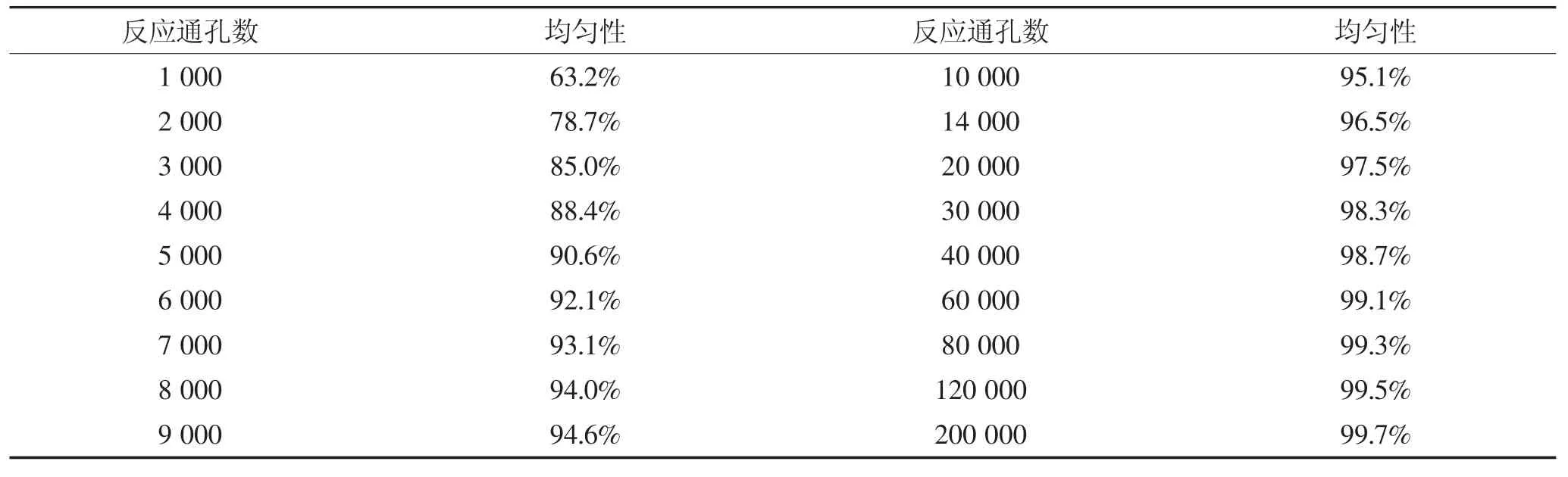
表2 目标粒子分布均匀性Table 2 The distribution uniformity of target particles

依据上述结果，可以得到最佳反应通孔数8 000或9 000对应的目标粒子分布均匀性为94.0%或94.6%；同时根据上述方法，可以得到满足指定要求的分布均匀性对应的最低反应通孔数，从而为cd－PCR的芯片设计提供了理论参数指导。另外，由表2同样可以发现，随反应通孔数的增多目标粒子分布均匀性逐渐增大，但当反应通孔数大于某值时，分布均匀性的增加将变得愈发缓慢（增速低于1%）并逐渐趋于饱和，由此同样可以得出最佳反应通孔数应为8 000或9 000的结论。

5 总结

利用C语言模拟了芯片数字PCR中目的核酸进入反应通孔的计算过程，并对cdPCR中干扰粒子对目的核酸分布的影响、检测目的核酸的最佳反应通孔数、目的核酸分布均匀性等问题进行了分析与计算，得到如下结论：

（1）在干扰作用完全随机的情况下，对于任意取值的反应通孔数，干扰粒子有无或其存在多少均不会破坏目标粒子的随机分布程度，因此，无论有无干扰粒子或其存在多少，目标粒子的N-Y曲线分布都将基本相同。

（2）在干扰作用完全随机的情况下，对于任意取值的反应通孔数，无论有无干扰粒子或其存在多少，检测目标粒子的最佳反应通孔数与目标粒子个数之比都应为 8∶1 或 9∶1。

（3）当目标粒子个数为1 000时检测目标粒子的最佳反应通孔数为8 000或9 000，而对应的目标粒子分布均匀性为94.0%或94.6%。