含几何偏心误差的变双曲圆弧齿线圆柱齿轮动力学分析
2020-09-14陈帅,祝杰,侯力,吴阳
陈 帅,祝 杰,侯 力,吴 阳
(1.四川大学制造科学与工程学院,四川 成都 610065;2.二滩水力发电厂,四川 攀枝花 617100)
1 引言
变双曲圆弧齿线圆柱齿轮(VH-CATT)作为一种新型齿轮,在齿宽方向的齿线为圆弧齿线,中截面上的齿廓线为渐开线,其他截面上的齿廓线为变双曲线,具有接触性长、无轴向分力、承载能力大、传动效率高、传动平稳等特点,故有广阔的应用前景。20世纪40 年代,文献[1]提出了弧齿圆柱齿轮的概念。许多学者对其理论进行了深入研究,文献[1]对面向制造的弧齿圆柱齿轮的成型原理和三维建模进行了较深入的剖析;文献[2]对圆弧齿轮的静态接触应力进行了详细的研究。文献[3-4]对圆弧齿轮的动态接触应力接行了详细的分析。但目前对于变双曲圆弧齿线圆柱齿轮加工误差的研究甚少。而齿轮在制造与安装的过程中,难以避免地会产生误差,从而使齿轮副的瞬时传动比发生变化,产生传动误差;会大大降低齿轮工作的可靠性与精度,甚至严重时导致齿轮或其他零件的损坏,从而使传动系统失效而导致严重后果[5]。因此对齿轮特别是对于变双曲圆弧齿线圆柱齿轮而言传动误差的研究是非常有必要的。文献[6]从啮合线增量与几何偏心关系入手,详细推导分析几何偏心对渐开线齿距累积误差的影响规律,分析方式简单明了被广泛引用。文献[7]从加工角度系统的分析了齿轮误差的成因。文献[8]建立了齿轮误差模型并进行了仿真分析,但不能精确描述出齿轮偏心对系统传动的影响规律。
目前对于齿轮传动误差的研究主要集中于齿轮误差曲线与减小传动误差方法,但是齿轮传动误差对齿轮传动的影响是直接由齿轮转角变化决定的。采用ADAMS 对含有几何偏心误差的变双曲圆弧齿线圆柱齿轮进行动力学仿真,通过对该齿轮传动转角误差的分析,与传统理论计算方法得到的结果进行对比,研究几何偏心误差对变双曲圆弧齿线圆柱齿轮传动的影响规律。
2 含几何偏心误差的变双曲圆弧齿线圆柱齿轮模型的建立
几何偏心是产生齿轮传动误差的重要来源,在变双曲圆弧齿线圆柱齿轮切削过程中,齿坯在旋转刀盘上进行加工的过程中,工件孔轴线与刀具轴线发生周期性的变化,继而使工件在切制时,实际回转中心偏离了理论回转中心。根据齿轮几何偏心误差的成因,可以建立含几何偏心误差的变双曲圆弧齿线圆柱齿轮三维模型。变双曲圆弧齿线圆柱齿轮的成形原理,如图1 所示。

图1 VH-CATT 加工示意图Fig.1 Processing of VH-CATT
完成加工的运动包括:(1)采用旋转刀盘来进行加工,装有刀头的刀盘安装在主轴上进行圆周旋转运动,即主运动。(2)待加工的工件(齿坯)安装在工作台上做旋转运动。刀盘沿齿轮分度圆切向移动,刀盘与工件实现精确的展成运动。完成齿面的形成过程。(3)在加工过程中,刀盘的进刀、退刀运动,和齿坯的分度运动。VH-CATT 齿面形成过程通过齿坯与刀具的形成原理和啮合原理,基于由刀具旋转形成的空间曲面方程,经过坐标变换,得到该齿轮轮齿齿面方程[1](1)。
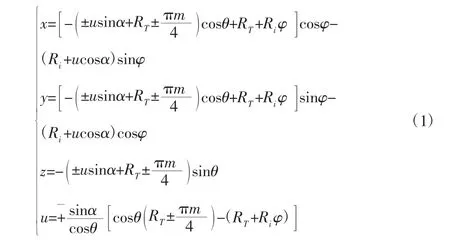
式中:RT—名义旋转刀盘半径;Ri—齿坯分度圆半径;m—齿轮模数;u—刀具曲面上任意点沿刀刃到参考点位移(mm);α—刀具压力角(°);φ—齿轮的转角,顺时针方向为正;θ—加工过程中刀具从齿坯中截面到端面的转角(°)称为齿廓位置角,顺时针方向为正;±—取正号时表示凹齿面,取负号表示凸齿面。
在齿轮切削加工过程中,齿轮的回转中心线与刀具之间的距离不变,加工出来的齿轮基圆、节圆也不变。加工的回转中心线与安装使用的回转中心线不重合,会导致基圆中心与齿顶圆上各点之间的距离不等,在精确齿轮模型的基础之上,根据上述分析建立含几何偏心误差的变双曲圆弧齿线圆柱齿轮模型。参照齿面方程1,运用MATLAB 取点计算得到凹、凸齿面的数据点云,然后将这些点云导入到UG 里面,经过一系列的操作得到变双曲圆弧齿线圆柱齿轮的齿面三维模型,然后以O 为圆心。为齿顶圆半径,以为齿根圆半径,经过一系列操作建立初始的变双曲圆弧齿线圆柱齿轮标准模型;再利用布尔运算以偏心距e 的O1为圆心切除半径之外的部分;通过装配建立对应的传动副模型;最后得到含几何偏心误差的变双曲圆弧齿线圆柱齿轮传动副三维模型,如图2 所示。

图2 含几何偏心误差的齿轮模型Fig.2 Gear Model with Geometric Eccentricity Error
3 几何偏心误差对齿轮传动精度的影响
目前,对于齿轮传动误差分析主要采用的是啮合线增量法。将齿轮转角变化产生的误差看作是轮齿间啮合线增量的变化。齿轮加工误差成因很多,不同误差源在加工过程中所引起齿轮间啮合关系的变化规律互不相同,几何偏心误差在齿轮加工误差中占有很大比重。几何偏心反映为齿轮加工的回转中心线与安装使用的回转中心线不重合,二者的偏心量用e 表示。由于变双曲圆弧齿线圆柱齿轮齿轮的中截面齿廓为渐开线齿廓[1]。采用几何偏心齿轮与标准齿轮做单面啮合,在任意位置,啮合线增量可以表示为:
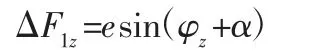
式中:α—压力角,单位为弧度(rad);φz—逆时针转过的角度,单位为弧度(rad)。
可以看出,啮合线的变化规律符合正弦变化规律,周期为2π。根据渐开线的性质,得到该齿轮的转角误差为:

式中:Δφ—几何偏心引起的转角误差,单位为mm;rb—从动齿轮基圆半径,单位为mm。
建立四对含几何偏心误差的单级变双曲圆弧齿线圆柱齿轮传动系统模型,各对齿轮的基本参数,如表1 所示。其中,0 号与1号啮合,0 号与2 号啮合,0 号与3 号啮合,0 号与4 号啮合。
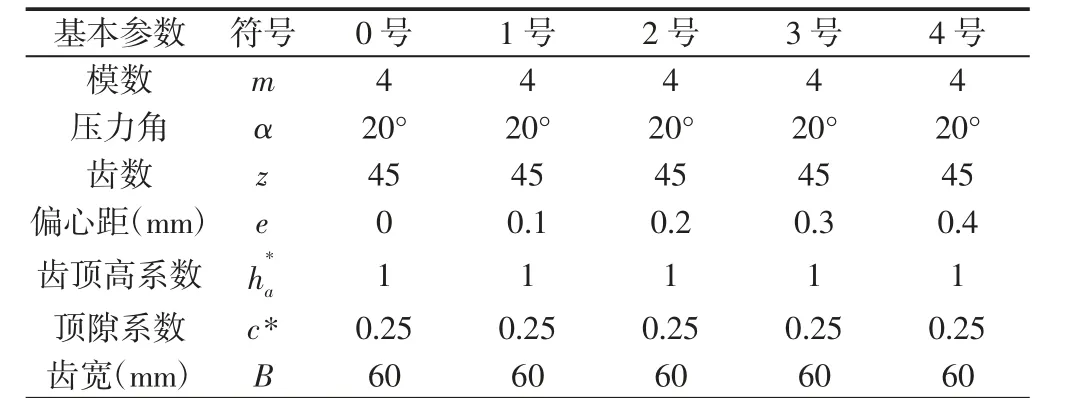
表1 偏心齿轮基本参数Tab.1 Basic Parameters of Eccentric Gear
4 ADAMS 仿真分析及结果处理
4.1 ADAMS 仿真预处理
ADAMS 是使用交互式图形环境的多体动力学仿真软件,可以从静力学、运动学、动力学方面来对虚拟机械系统进行分析。目前,ADAMS 被广泛应用于齿轮啮合分析中。在UG 中将建立的含有几何偏心误差的变双曲圆弧齿线圆柱齿轮三维装配体模型选择导出Parasolid 格式文件,该文件格式可以防止数据丢失,保证导入到ADAMS 中模型的准确性,从而保证仿真结果的正确性和有效性。为了控制插值分析中的插值误差,同时为了尽可能的减少仿真的计算时间,仿真设置中采用系统默认的积分误差。采用Intergrator选项来改变积分方式,选择Gstiff 积分求解器,积分格式为S12,积分精度为0.001。具体的仿真参数选取,如表2 所示。表格中各参量的单位按ADAMS 中默认的MMKS 单位,为了降低分析中振动对仿真结果的影响,阻尼系数选择较大值,此处选择为500。
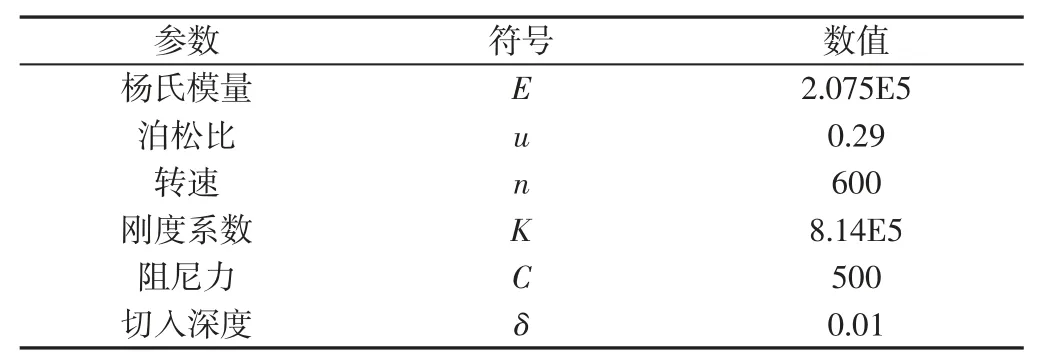
表2 仿真参数的设置Tab.2 Setting of Simulation Parameters
4.2 ADAMS 仿真结果处理与分析
根据齿轮间的运动关系,共定义了2 个转动副,1 个接触,1个驱动,1 个扭矩负载,得出最终的含几何偏心误差的变双曲圆弧齿线圆柱齿轮虚拟样机,然后在ADAMS 中建立主动轮和从动轮的转角测量Measure。ADAMS 软件能够直接得到主从动轮各个时刻转角的变化,主动轮转速恒定,转角为φ1,单位为弧度(rad)。由于其存在几何偏心误差,会使从动轮产生转角误差,转角为φ2,单位为弧度(rad)。从动轮的实际角位移与理论角位移做差即可得到从动轮的转角误差,假设传动比为i,那么可以得到从动轮的转角误差Δφ2(rad)为:
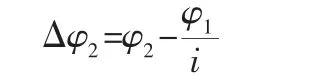
此处为方便计算,选取i=1,即 Δφ2=φ2-φ1。
将ADAMS 仿真得到的主从动轮转角数据导入到MATLAB中,进行数据处理后得到转角误差数据,重新导入到ADAMS 后处理得到各从动轮对应的转角误差曲线,如图3 所示。
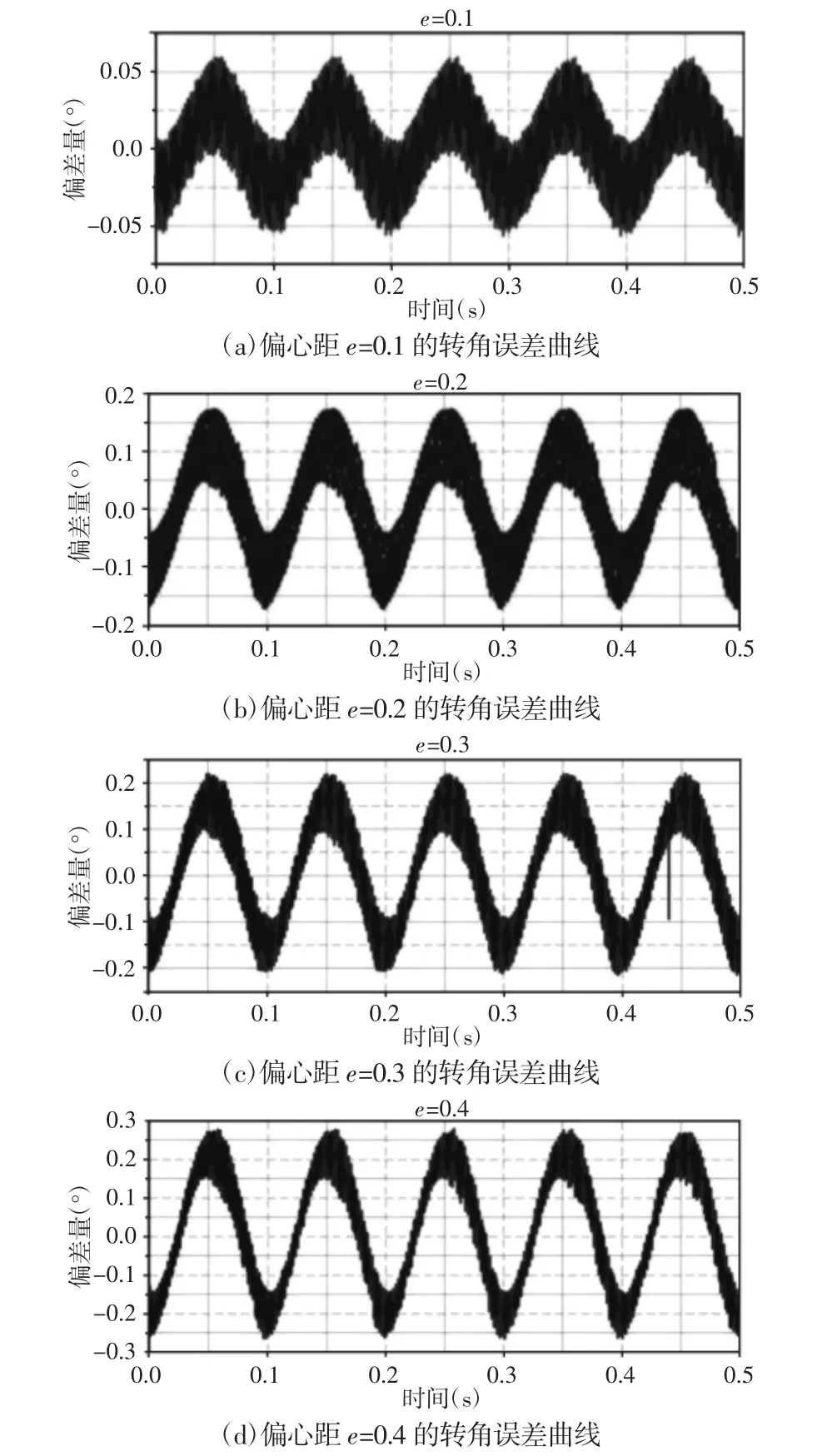
图3 转角误差曲线Fig.3 Angle Error Curve
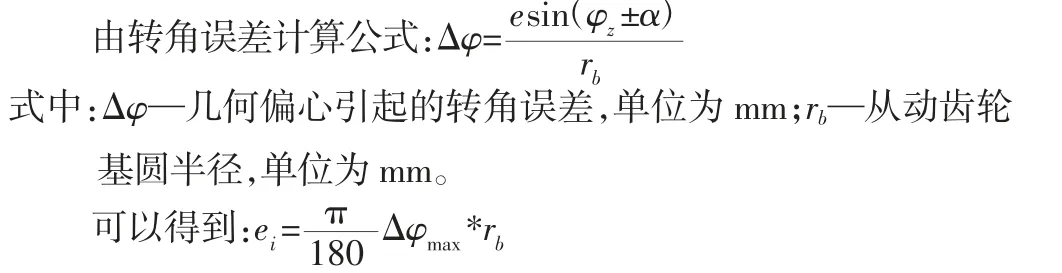
式中:Δφmax的单位是角度制(deg);ei—计算得到的几何偏心误差,单位为mm。
将基圆半径rb和最大转角误差Δφmax带入,计算可以得到经ADAMS 仿真后的变双曲圆弧齿线圆柱齿轮几何偏心误差值,再与理论几何偏心误差值进行对比可以得到相对偏差量,具体数据,如表3 所示。由表3 可以得到:(1)由基圆半径和最大转角误差计算得到的仿真几何偏心误差计算值与几何偏心理论值的相对偏差量较小,估计精度较高。(2)从ADAMS 仿真分析角度验证了转角误差理论计算公式在变双曲圆弧齿线圆柱齿轮上应用的正确性。即几何偏心最大转角误差等于偏心距与基圆半径的比值。
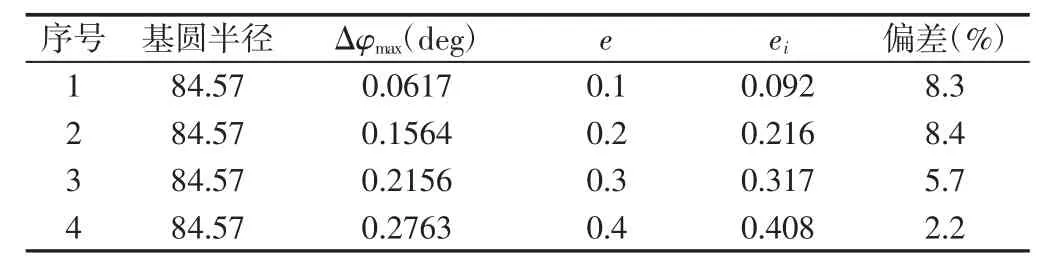
表3 几何偏心计算值Tab.3 The Calculated Value of Geometric Eccentricity
5 结论
(1)用ADAMS 仿真分析得到的几何偏心误差计算值与几何偏心理论值偏差的相对偏差量较小,估计精度较高。同时验证了理论计算方法的正确性,即变双曲圆弧齿线圆柱齿轮的最大转角误差等于几何偏心值与其对应的从动轮基圆半径的比值。(2)利用ADAMS 通过转角误差来计算几何偏心误差的方法,可以通过测量动态传递误差来间接计算变双曲圆弧齿线圆柱齿轮的几
何偏心值。为以后分析变双曲圆弧齿线圆柱齿轮的加工误差具有重要的指导意义。
