不等半径减振器叠加阀片的变形解析计算

孙未 张力云 李灿 刘钟科 郭长红

（1.成都理工大学，核技术与自动化工程学院，成都 610059；2.成都迈科创科技有限公司，成都 610015；3.四川宁江山川机械有限责任公司，成都 610106）

主题词：减振器 不等半径 叠加阀片 解析计算

1 前言

减振器的性能对车辆的行驶安全性、乘坐舒适性和操纵稳定性具有重要的影响[1-3]。车用双筒液力减振器各阀系的弹性阀片通常由多个阀片叠加构成，叠加阀片的参数对阀片变形量和阀开口值具有重要影响，因此其参数设计尤为重要[4]。对于阀系采用阀片叠加结构模型的减振器，阀片的变形解析计算一直是其参数化建模的难点。目前国内外学者主要基于小挠度变形理论和大挠度变形理论对减振器叠加阀片的力学模型、阀片的变形及阀开口值的计算方法等基础理论展开了研究[5-6]。李仕生[7]等人分别基于弹性力学原理对小挠度理论进行了深入的研究，并将其解析解应用于阀片计算。康雨[8]、韦勇[9]等人分别基于大挠度理论对节流阀片的变形进行了研究，推导出阀片大挠度变形与其半径的关系式，获得了筒式减振器环形阀片弯曲变形的大挠度变形与半径的关系。赵雷雷[10]等人对减振器变厚度阀片变形计算及应力解析计算进行了研究，建立了相应的解析计算式和应力解析计算方法。戎红俊[11]等人用AMESim 建立了一套仿真模型，并基于该模型研究了常通孔节流面积、复原孔节流面积、阀片刚度、开阀压力和活塞缝隙等几个关键设计参数对减振器动态特性的影响情况。针对不等半径叠加阀片的研究，康雨[8]等人建立了外半径不全相等时环形叠加阀片的力学模型，用大挠曲变形解析方法与有限元分析相结合的等效模型求解方式推导出该环形叠加阀片挠曲变形的解析式，Ding[12]等人建立了两片不等半径阀片叠加模型，研究了两片阀片的半径比和厚度比与阀片变形量之间的关系，但没有得出不等半径叠加阀片变形的通用解析计算式。尽管采用有限元软件可以对不等半径叠加阀片变形进行仿真，但该方法不能提供任意不等半径叠加阀片变形解析式，不可用于设计计算，不能满足对阀片进行精确设计和特性分析的要求。

本文对减振器的油液压力进行必要简化，假设被研究区域内同一时刻压力处处相等，研究在小挠度变形情况下，不等半径叠加阀片在均布压力下的变形。结合其力学模型，利用阀片变形微分方程及边界约束条件和变形连续性条件，对阀片的变形解析计算方法进行研究，并通过实例进行解析计算和ANSYS 仿真，验证模型的正确性。

2 不等半径叠加阀片的变形微分方程

2.1 阀片力学模型

如图1 所示，双筒液力减振器主要由复原阀、流通阀、压缩阀和补偿阀构成。

图1 双筒液力减振器模型

各阀系采用不等半径叠加阀片模型，其在均布压力下的力学模型如图2 所示，阀片的内圆为固定约束，有效内圆半径为ra，外圆为自由约束，最大外圆半径为r1，ri为第i片阀片的最大外半径，阀片总数为n，所受均布压力为P。

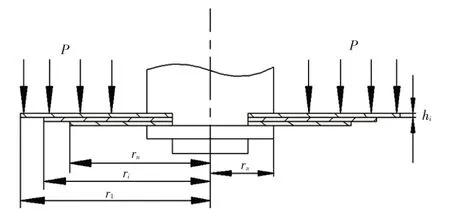
图2 不等半径叠加阀片在均布压力下的实际力学模型

根据叠加阀片的叠加原理[13]可将图2所示的实际力学模型进行等效处理，如图3 所示，其中叠加阀片的等效厚度he为：

式中，hi=δih为第i片阀片的厚度；δi为第i片阀片的厚度系数；h为阀片的基准厚度。

n=1时为单片节流阀片模型，本文不再分析。

图3 不等半径叠加阀片在均布压力下的等效力学模型

2.2 阀片变形微分方程

不等半径叠加阀片在均布压力下的变形示意如图4 所示，其中fr为半径r处的变形量。

图4 不等半径叠加阀片在均布压力下的变形示意

阀片的结构、载荷及变形均关于Z轴（Z为阀片轴向坐标）对称，因此根据弹性力学可得阀片的变形曲面微分方程[14-15]：

将式（1）带入D的表达式，可得阀片在任意半径r处的弯曲刚度为：

2.3 阀片变形微分方程的解

Ai、Bi、Ci、Ti可由叠加阀片在内圆为固定约束和外圆为自由约束的边界条件，以及在半径ri处的连续条件确定：

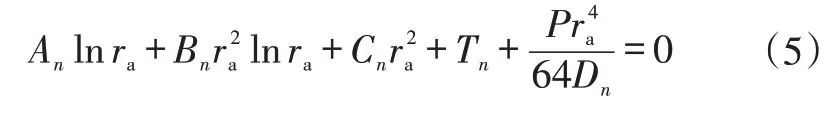
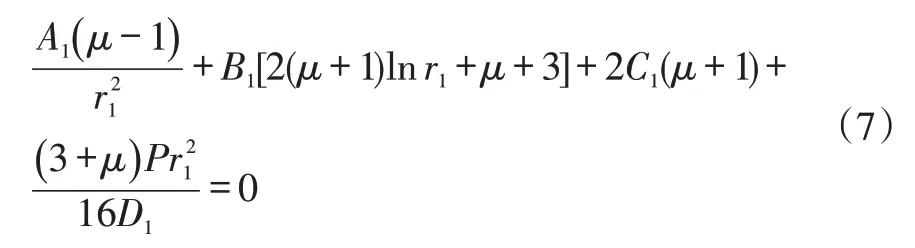
e.半径ri(2≤i≤n)处的变形连续，即可得：

f.半径ri(2≤i≤n)处的变形斜率相等，即，可得：

g.半径ri(2≤i≤n)处的剪力相等，即可得：

h.半径ri(2≤i≤n)处的弯矩相等，即，可得：

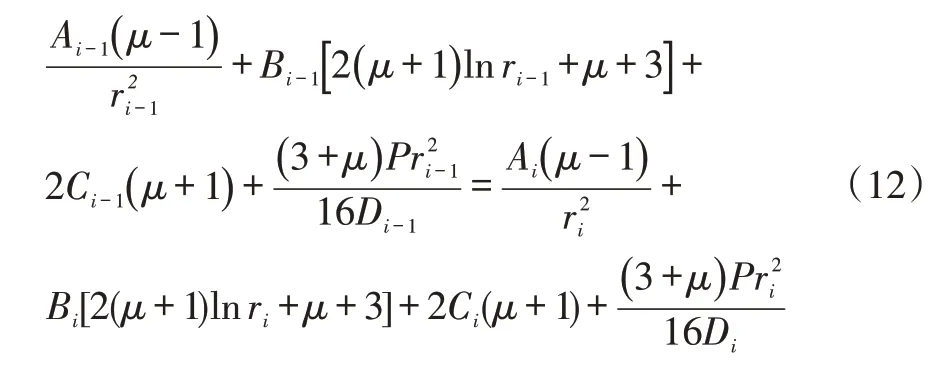
由式（5）～式（12）可以求得不等半径叠加阀片在均布压力作用下的弯曲变形微分方程通解中的Ai、Bi、Ci、Ti，从而得到微分方程的通解表达式。

2.4 阀片变形解析计算式

将求得常数代入式（4），便可以得到不等半径叠加阀片在任意半径处的变形解析式。分析可知，解析式各项均含有公因子P/h3，将式（4）提取公因子P/h3，其余项定义为常数Gr，则不等半径叠加阀片在任意半径r处的变形量可表达为[16-17]：

式中，Gr为不等半径叠加阀片在均布压力作用下半径r处的变形系数，与阀片的结构、弹性模量、泊松比、半径位置及半径差有关。

3 不等半径叠加阀片的变形解析计算与仿真验证

3.1 阀片的变形解析计算

设n=3、h=0.4 mm、μ=0.3、E=200 GPa、δ1=1、δ2=3/4、δ3=1/2，针对表1 所示的4 种半径差（0.5 mm、1.0 mm、1.5 mm、2.0 mm）尺寸方案进行分析。

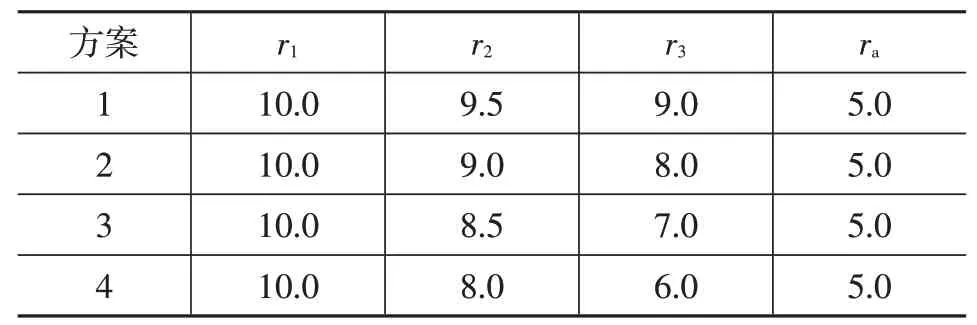
表1 4种半径差的叠加阀片的尺寸参数 mm

不同半径差的叠加阀片的变形系数Gr随半径r的变化曲线如图5所示。

图5 不同半径差的叠加阀片的变形系数随半径r的变化曲线

求得Gr后，根据式（13）求得模型在受均布压力P分别为2 MPa 和3 MPa 条件下[18]任意半径r处的变形量fr，不同半径差叠加阀片的变形量随半径r的变化曲线如图6所示。

3.2 仿真验证

利用ANSYS 有限元软件建立仿真模型，边界条件与图2 所示的力学模型一致。分别对叠加阀片施加2 MPa 和3 MPa 均布压力，阀片之间施加无摩擦（Frictionless）接触，对其进行仿真分析。方案1、方案3的变形仿真云图（显示效果放大15倍）如图7、图8所示。

图6 不同均布压力下不同半径差的叠加阀片的变形量随半径r的变化曲线

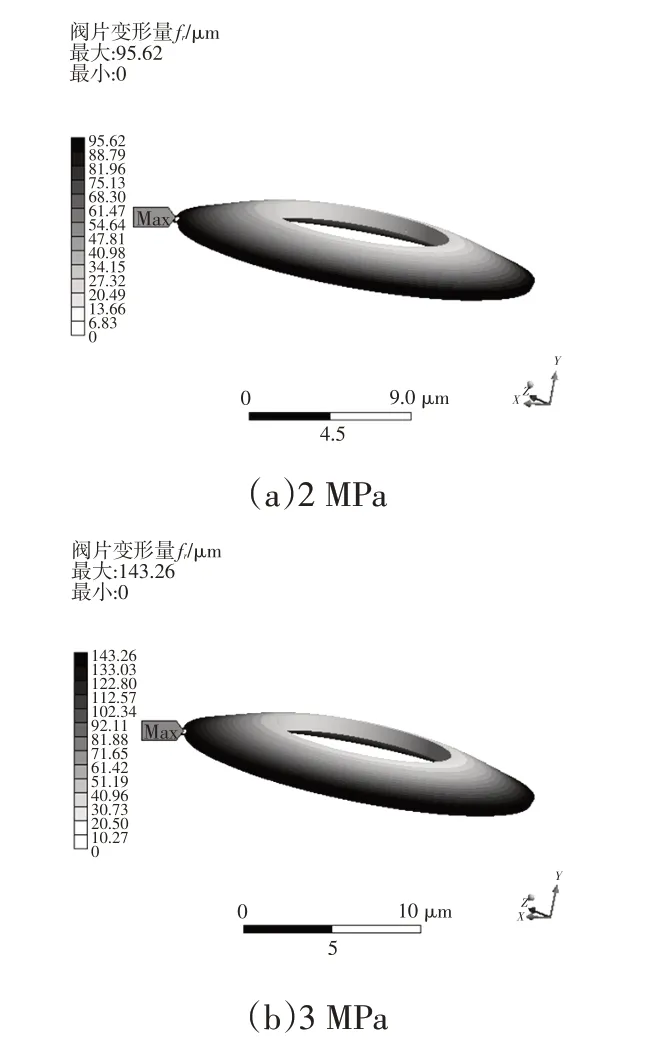
图7 不同均布压力下半径差为0.5 mm的叠加阀片仿真结果

3.3 对比验证与误差分析

4 种方案叠加阀片在半径r处的最大变形量fr的解析值与ANSYS仿真计算值对比分析结果如表2所示。

从表2可以看出，当不等半径叠加阀片的半径差值小于1.5 mm时，其解析值和仿真值相差不大，相对误差在1%左右。结果表明，不等半径叠加阀片的解析式正确，误差的主要来源为不等半径叠加阀片的网格划分、模型的简化以及计算精度等。

图8 不同均布压力下半径差为1.5 mm的叠加阀片仿真结果

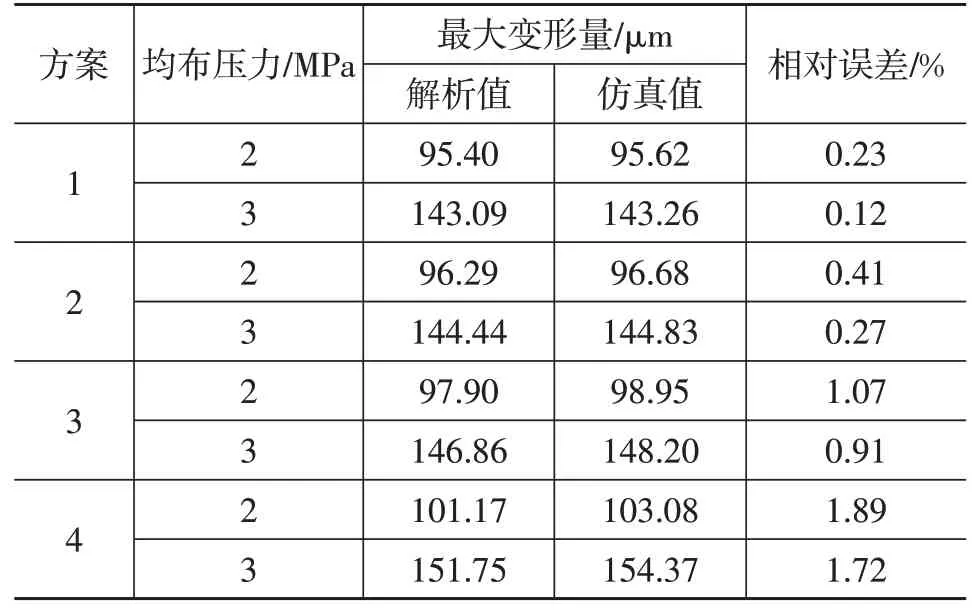
表2 不等半径叠加阀片最大变形量fr的解析值与仿真值对比

从表2还可以看出，当不等半径叠加阀片的半径差值达到2.0 mm时，其解析值与仿真值的误差增大，主要是由于该变形达到大挠度变形，所以计算误差增大。

4 结束语

本文对均布载荷作用下的不等半径叠加阀片的变形解析计算方法进行研究，得到了阀片弯曲变形曲面微分方程的通解，可以求得阀片在任意半径r处的变形量。在小挠度变形条件下，其变形量的解析计算值与ANSYS 仿真结果的误差在1%左右，但在大挠度变形条件下，该解析式的计算结果误差增大。