基于最优化理论的特大跨悬臂浇筑拱桥施工阶段拱圈节段浇筑长度分析
2020-09-07田仲初张祖军
郑 浪,田仲初,张祖军
(1.湖南交通职业技术学院,湖南 长沙 410004; 2.长沙理工大学 土木工程学院,湖南 长沙 410015)
臂浇筑拱桥作为我国近10 a新兴的拱桥施工工艺,我国学者对其进行了较为系统的研究,文献[1]-[2]中,吴欣、王祺顺等人研究了悬臂浇筑施工过程中施加临时预应力后与索力的耦合效应;文献 [4]中,周超基于最优化理论及 “一次张拉到位”的思想,利用ANSYS求解了施工阶段最优索力并分析了索力敏感性因素;文献 [5]中卢云贵等人对施工过程中索力、截面应力、扣塔偏位的控制方法进行了分析研究;胡大琳等人基于最小弯曲能量法对施工阶段索力进行了优化,以达到降低拱圈截面应力的目标。
综上,我国悬臂浇筑拱桥研究已取得相当成果,尤其在索力优化领域,研究成果有效指导了实际工程的施工及监控,达到了通过调整索力优化拱圈截面应力的目标。但调索改善截面应力方式具有一定的局限性[6-8],如跨径过大、节段自重较重时,调整索力可能达不到理想的效果,且一味增大索力会造成扣塔局部应力集中,不利于结构安全[9-10]。本文基于最优化理论,以某在建的特大跨悬臂浇筑拱桥为研究对象,通过优化拱圈节段悬臂浇筑长度,探讨其对索力及拱圈截面应力的影响规律,该项研究成果可为同类型工程施工及监控提供一种新的思路。
1 最优化理论
在实际工农业等生产活动及科学研究中,我们会遇到很多优化问题,这些优化问题绝大部分不是单一目标存在,而是多个目标之间相互联系,相互影响。在多个目标之间找到一个平衡,取得最优解的方法,称为多目标优化方法。其数学模型如下:

式中:J表示目标函数,xi表示设计变量;gj、hk、wl为状态变量;N表示设计变量的总数目,m1+m2+m3表示状态变量的总数。
在多目标问题求解时,由于复杂的约束条件与目标函数之间相互耦合,因此很难求得最优解。目前常用的方法是将有约束的优化问题转换为无约束的优化问题,引入罚函数为实现这一算法的有效途径,数学表达式为:
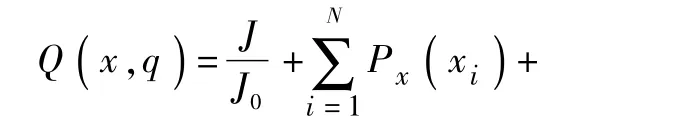
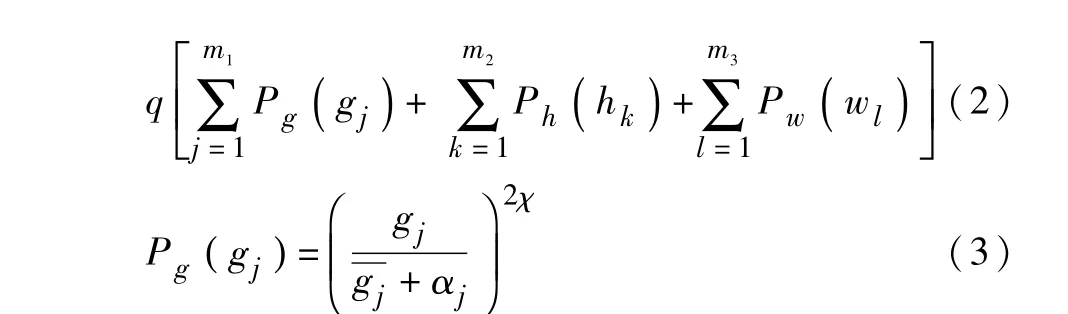
式(2)、式(3)中:J0为目标函数;q为约束条件;Px为设计变量的外罚函数;Pg、Ph、Pw分别表示状态变量的混合罚函数;χ为某一整数;αj为容许误差。
当所有设计变量均满足约束条件时,则根据罚函数,有Px(xi)=0,此时式(2)则可表述为:
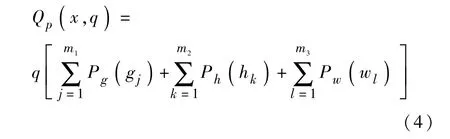
引入罚函数后,将多目标有约束问题转换成无约束问题,再基于共轭梯度法确定搜索方向,迭代公式如下:

2 工程概况
本文研究对象为一在建钢筋混凝土拱桥,主桥采用斜拉扣挂悬臂浇筑施工工艺。拱圈净跨径240 m,净矢高40 m,净矢跨比1/6,拱轴系数m=1.85,混凝土截面宽10 m、高4.5 m,主拱圈混凝土标号为C60,拱圈沿桥轴线方向分为2个托架现浇段 (拱脚位置),34个悬臂浇筑段,1个合龙段 (拱顶)。拱圈顶、腹、底板均为变高设计。桥型布置图及斜拉扣挂节段划分示意图见图1、图2。

图1 桥型立面布置图 (单位:cm)Figure 1 Bridge façade layout(Unit:cm)
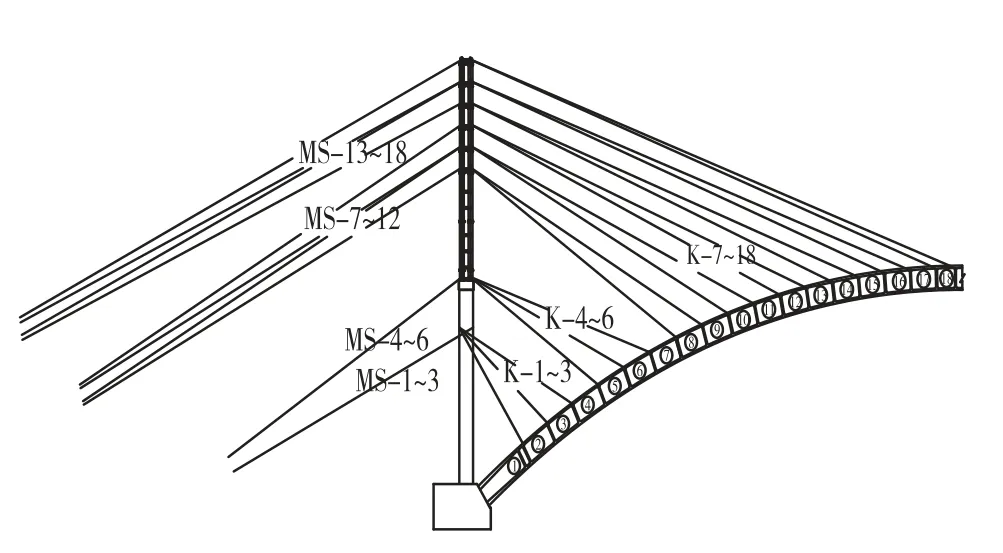
图2 节段划分示意图图 (单位:cm)Figure 2 Schematic diagram of segmentation(Unit:cm)
3 优化数学模型及有限元模型建立
a.目标函数的选取:拱桥在悬臂浇筑过程中,其控制性指标为拱圈节段截面应力水平,故选取主拱圈各节段应力平方和最小为目标,构建目标函数如下:

b.设计变量的选取:以各节段悬臂浇筑长度lni为设计变量。
c.约束条件的选取:
① 主拱圈施工过程中应保证截面最大拉应力应小于混凝土抗拉强度设计值,f≤1.96 MPa。
②根据规范要求,扣索应力应留有2.5倍安全系数富余,即σs≤744 MPa。
使用ANSYS APDL建立该桥参数化有限元模型 (见图3),主拱圈及交界墩使用Solid65三维实体单元模拟,扣、锚索采用杆单元LINK10模拟,扣塔构件采用梁单元Beam188模拟;两拱脚及交界墩底采用固结约束方式,锚索在锚锭处模拟为固结,扣塔立柱与横向联系间设置虚拟刚性梁。扣索扣点与主拱圈实体单元共节点。因主拱圈截面为实体单元,不便施加集中力和集中弯矩,在每个节段浇筑分界面处设置质量节点MASS21作为加载节点,然后将节段浇筑分界面连同质量节点联系截面刚化,将集中力和集中弯矩施加于加载节点,拱圈节段长度与扣点位置以参数数组的形式表示,以方便后继优化。
使用ANSYS中的 “单元生死功能”模拟悬臂浇筑施工过程。网格划分采用六面体扫掠、映射划分和四面体自由划分相结合的方法,在扣点处加密,远离扣点的位置网格可适当稀疏一些。

图3 有限元模型示意图Figure 3 Diagram of the finite element model
4 优化计算结果
使用MATLAB工具箱编制悬臂浇筑长度形lni优化程序,借助MATLAB强大的矩阵计算能力,寻求数学最优解,并将优化结果导入ANSYS程序中,将ANSYS仅当求解器使用,调用其 “batch”批处理模式,在后台同时运行多个指定的命令文件,根据ANSYS输出的有限元计算结果,MATLAB程序继续执行矩阵运算,如此反复,直至收敛于最优解,收敛误差为ANSYS中默认执行的
1E-6。
经MATLAB搜索收敛于最优解,提取设计变量结果如下:
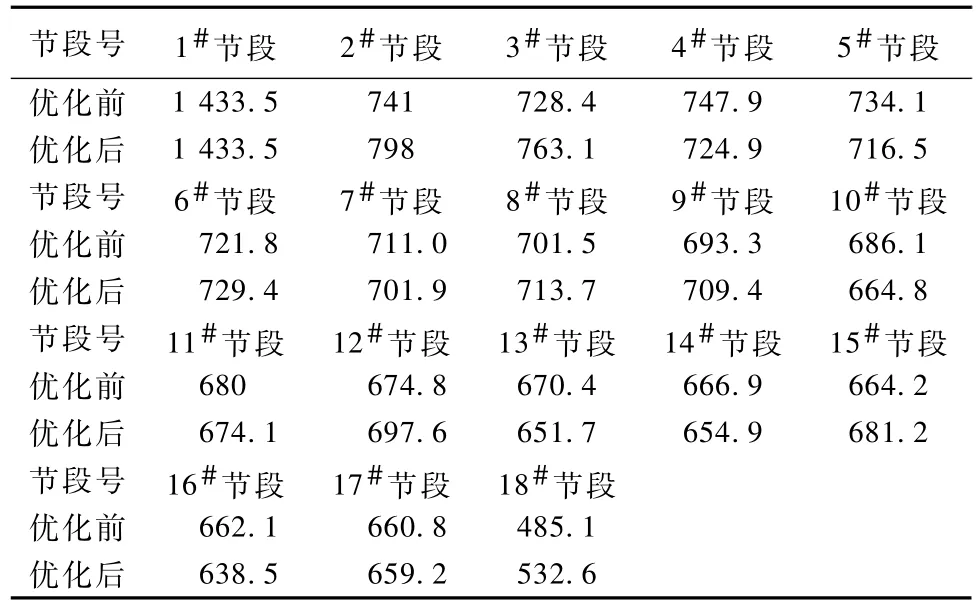
表1 优化后设计变量计算结果表Table 1 Calculation result calculation table after optimization cm
将优化后的设计变量导入ANSYS中关于节段悬臂浇筑长度的数组中重新赋值,设置相应荷载步,耦合对应节段扣索索力,对结构进行施工阶段分析。
4.1 优化后施工阶段扣索索力结果
由于节段悬臂浇筑长度的变化,扣索索力也会随之发生变化,提取优化后各节段施工过程中最大索力值,如图4、表2所示 (以西岸半跨为例)。

图4 优化前后悬臂浇筑过程扣索索力峰值对比图 (单位:kN)Figure 4 Comparison of peaks of cable tensions during cantilever casting before and after optimization(Unit:kN)
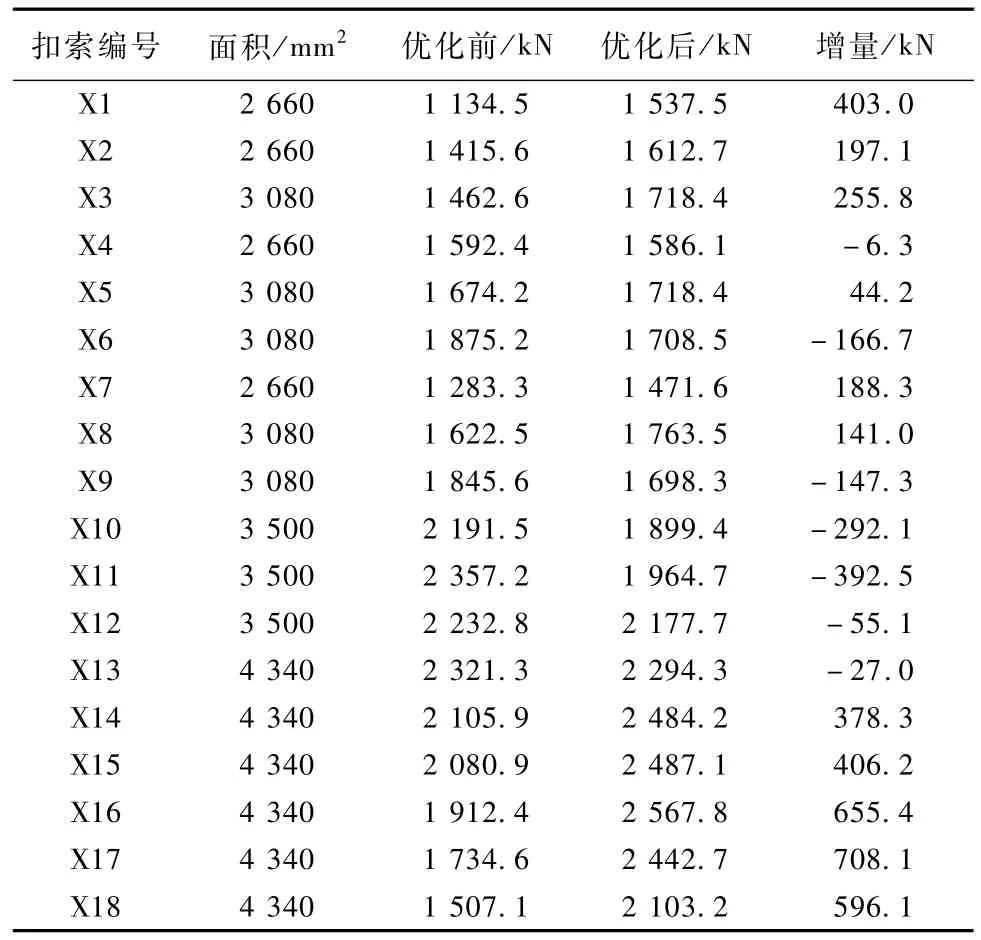
表2 优化前后扣索索力值对比表(单位:kN)Table 2 Comparison of the cable strength values before and after optimization(Unit:kN)
优化计算结果表明:由于拱圈节段长度的变化,扣索索力刚度影响矩阵也随之变化,对扣索索力值有较大影响。调整拱圈节段悬臂浇筑长度后,大部分扣索索力值增幅较为明显,其中变化最大的是17#扣锚索,增量708.1 kN,增幅40.8%,说明在原设计索力下,扣索处于低应力状态,未充分挖掘其承载能力,索力随拱圈节段浇筑长度变化后,大部分扣索索力值增大,且索力分布也更为均匀,较好利用了材料性能。
4.2 优化后施工阶段拱圈截面应力结果
施工节段拱圈截面拉应力为悬臂浇筑拱桥施工控制性指标,它决定了悬浇过程中拱圈的安全性、耐久性等,故本文目标函数为悬臂浇筑节段拱圈各截面拉应力平方和,在ANSYS中提取各施工阶段下截面最大应力,由于靠近扣点的混凝土单元存在应力失真现象,根据圣维南原理,选取每个拱圈节段中间断面,求得各断面顶底板最大拉应力如图5、表3所示。

图5 优化前后顶底板最大拉应力对比结果 (单位:MPa)Figure 5 Comparison of maximum tensile stress of top and bottom plates before and after optimization(Unit:MPa)
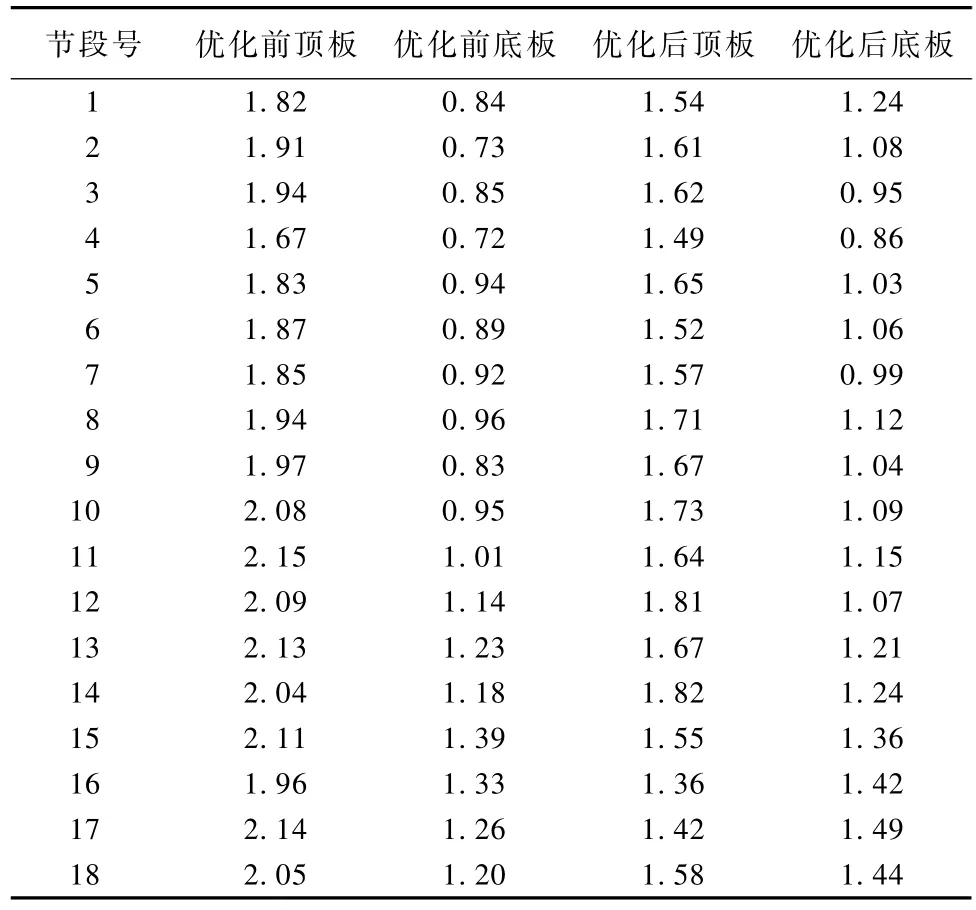
表3 优化前后拱圈节段最大拉应力Table 3 Maximum tensile stress of the arch ring segment before and after optimization MPa
以拱圈11#节段为例,其应力路径曲线及跨中截面应力云图6、图7所示。
计算结果表明:
a.优化前拱圈各节段截面拉应力水平普遍较高,顶板拉应力峰值达2.15 MPa,大于C60混凝土抗拉强度设计值1.96 MPa,拱圈在施工过程中存在开裂现象,对施工过程中结构强度及耐久性有不利影响;迭代优化后,顶板拉应力峰值显著降低,最大拉应力为1.82 MPa,降幅15.34%,小于抗力限制且有一定富余。

图6 应力路径曲线图Figure 6 Stress path graph
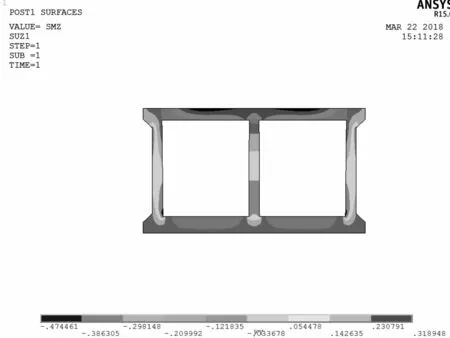
图7 截面应力云图 (单位:MPa)Figure 7 Cross-section stress(Unit:MPa)
b.优化后底板应力值较优化前有些许增大,应力增长后仍小于抗力限值且富余较大,结果在可接受范围内。
c.由图5可知,优化后拱圈截面顶底板应力差减小,应力流分布均匀,不存在截面应力流“断层跳跃”现象。
4.3 合龙工况应力对比结果
根据ANSYS优化结果,提取合龙工况下优化前后拱圈各截面应力值,并与一次成拱下拱圈截面应力进行对比,计算结果表明:优化调整后的拱圈应力线更逼近于一次成拱状态应力,截面应力分布得到良性改善,应力差明显减小,更接近于理想的均压状态,优化效果良好。
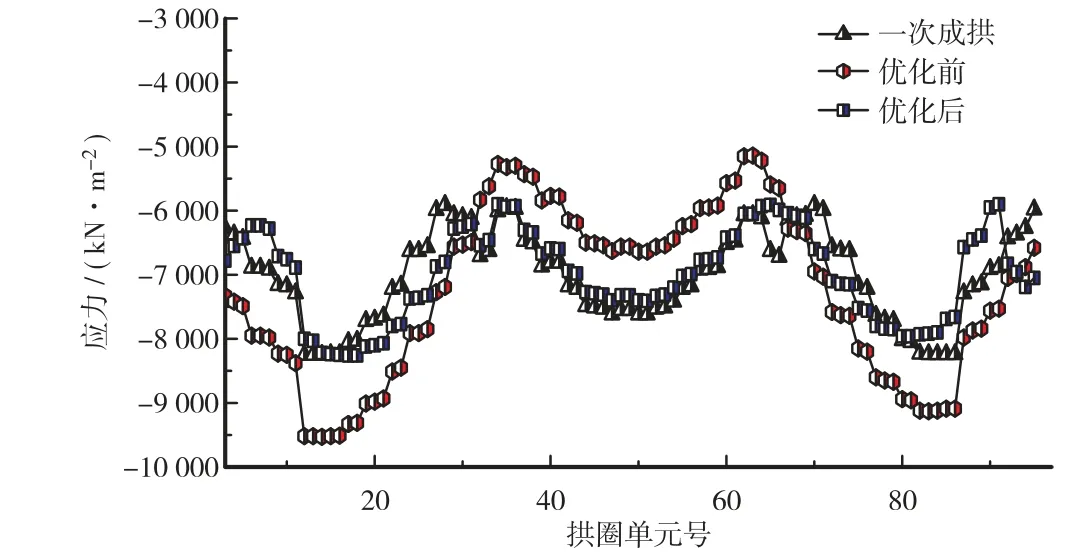
图8 合龙工况下拱圈截面应力线对比Figure 8 Comparison of stress lines of arch rings under closing conditions
5 结论
本文基于最优化理论,以某在建的特大跨悬臂浇筑拱桥为工程背景,建立该桥悬臂浇筑节段长度优化数学模型,并使用ANSYS求解了优化结果,可得到以下结论:
a.拱圈节段长度对扣索索力刚度矩阵有 “连带”影响,悬臂浇筑节段长度的变化,会显著影响施工过程中扣索索力峰值,在实际工程施工时应予以关注。
b.改变拱圈节段悬臂浇筑长度,对施工过程中截面应力峰值及分布有较大影响,以该桥为例,优化后拱圈顶板拉应力峰值显著降低,降幅15.34%,且应力流分布更为均匀。
c.改变拱圈节段悬臂浇筑长度,对拱圈成拱后截面应力线分布有一定影响,以该桥为例,优化后拱圈应力线更逼近于 “一次成拱”状态,应力差减小,接近均压状态。
