基于联合截面的圬工拱桥最小加固层分析

2018-08-28张文远

筑路机械与施工机械化 2018年6期

陈砚，张文远，李峰，向超

（1.中交第一公路勘察设计研究院有限公司，陕西西安 710075；2.西安市市政设施管理局，陕西西安 710064）

0 引言

在圬工拱桥加固过程中，只能通过拆除腹拱及填料或限制通行来卸掉二期恒载或活载，对于主拱圈恒载一般不予卸除［1］。这种加固特点就决定了圬工拱桥加固属于二次受力结构，即在二期恒载或活载加载前，新增混凝土加固层不会承担原拱圈的荷载，只有当二期恒载或活载加载时，新增混凝土加固层才开始参与受力。此种受力模式会导致加固层的应力、应变自始至终滞后于原拱圈的累计应力、应变，并且通常情况下原拱圈达到极限状态时，加固层的应力、应变可能还很低，当结构被破坏时，加固层可能达不到自身的极限状态，承载力得不到充分发挥。

圬工拱桥加固完成后，对加固效果的评定主要依靠荷载试验，即采用应变片对原圬工拱桥应变进行测量，最终确定其承载能力。但是，砌体材料为非匀质材料，测量所得应变很难真实反应结构受力状态。因此，本文通过对新旧拱圈内力及应力的分析，结合Midas Civil中施工联合截面的应用，确定最优加固层厚度并对圬工拱桥加固后的效果进行评价。

1 联合截面模拟的合理性

联合结构指由2种不同材料的构件或者同一种材料但强度和材龄不同的构件联合所构成的结构。Midas Civil中的联合截面处理主要是建立不同的施工阶段，并在适当的施工阶段将2种材料联合，即将加固层通过换算截面的方法换算成原圬工材料，然后根据2种构件的刚度和变形协调原理来分配构件的内力和应力，并考虑不同构件材龄引起的收缩徐变。此方法分析过程简单，同时可反映不同构件材料的时间依存性，从而简化结构计算和分析［2］。

2 截面受力及应力分析

设作用在原拱圈的恒载弯矩为M1，轴力为N1；二期恒载及活载弯矩为M2，轴力为N2；原截面高度为h1，面积为A1，惯性矩为I1；加固后的总高度为h2，总面积为A2，总截面惯性矩为I2。加固前后内力情况如图1所示［3－5］。

图1 加固前后截面的内力情况

2.1 恒载产生的应力

原拱圈恒载仍由原拱圈承担，计算原拱圈恒载的作用效应时采用原拱圈截面。

由原拱圈恒载弯矩和轴力引起的应力

式中：y为所求应力点到原拱圈截面形心处的距离。

截面的恒载应力分布如图2所示。

2.2 二期恒载及活载产生的应力

二期恒载及活载由原拱圈和新增拱圈组成的联合结构共同承担，计算二期恒载及活载的作用效应时采用联合截面。

由二期恒载及活载弯矩和轴力引起的应力

式中：y′为所求应力点到增大后的截面形心处的距离。

截面的二期恒载及活载应力分布如图3所示。

图2 恒载作用下的原拱圈截面应力状态

图3 二期恒载及活载作用下的截面应力状态

2.3 结合面混凝土收缩徐变应力

在混凝土和砌块黏结完好的情况下，由2种材料性能差别引起的变形差，将会使构件产生截面应力重分布和结构内力重分布，影响结构的变形、裂缝的出现和发展等使用性能，甚至影响极限承载力。相对于原结构，新增混凝土层将会产生收缩，使新、旧结合面处产生附加应力；徐变则是因为混凝土受压、长期变形增大导致新旧材料的变形差异。本文按照叠合梁的先后收缩差原理计算结构各部位的应力。混凝土收缩应变计算式为

式中：εcs（t，ts）为收缩开始时龄期（ts）到计算考虑的龄期（t）时的收缩应变；εcs0为名义收缩系数；βs（tts）为从龄期t到ts的收缩应变发展系数。

对原拱圈计算加固拱板收缩后产生的应力时，为了保证截面的变形协调性，设想在新增混凝土层的中心施加拉力N，以保持截面的变形协调，为了消除设想的拉力，再在同一位置上施加一数值相等的反向压力，如图4所示。

混凝土徐变应变计算见式（4），应力状态如图5所示。

式中：εc为徐变应变值；εe为加载时的弹性应变值；φ为徐变系数。

图4 收缩下的截面应力状态

图5 徐变下的截面应力状态

2.4 总应力

截面上的应力σ是由恒载应力和活载应力叠加在一起的。由于原拱圈恒载在新增截面处没有应力，所以在新增加固层和原拱圈的结合面处将会有应力突变。截面总应力分布如图6所示。

图6 截面总应力

3 工程概况

本文依托国道316线上的土沟中桥（图7）加固工程，采用Midas Civil中施工联合截面计算方法对原拱圈应力进行分析。

图7 土沟中桥立面

土沟中桥为单孔空腹式圬工拱桥，跨径20m，桥面净宽为7m，净矢高4.05m，拱圈厚65cm。拟采用增大截面法对既有桥梁进行加固，即分别采用10～60cm拱板以10cm为一级进行变高加固。通过应力比对，选取合理的加固层厚度。

在建模过程中，原拱圈材料根据规范采用细石料、半细石料砌体和M20号砂浆，加固层采用C30混凝土。

建模时，拱上填料的传力模拟是关键点，采用立柱单元进行传力模拟，此单元用梁单元进行模拟，不考虑面外荷载效应，所以可以对它采用释放梁端的约束进行等效传力模拟。

4 强度计算结果

根据计算，分别列出不同加固层厚度下原拱圈的拱脚和拱顶上下缘在恒载、活载、收缩徐变作用下产生的应力，分析加固层厚度对主拱圈上下缘应力的影响。

4.1 加固后原拱圈截面的恒载应力

加固后原拱圈在恒载作用下的应力如表1、图8所示。

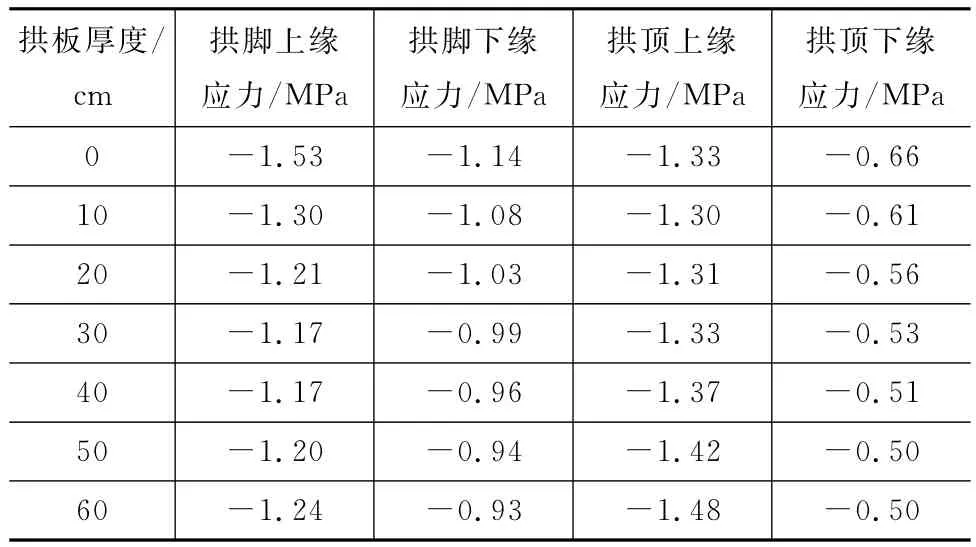
表1 加固后原拱圈在恒载作用下的应力值

图8 加固后原拱圈在恒载作用下应力值与加固层厚度的关系

通过表1、图8发现，加固后原拱圈在恒载作用下拱脚、拱顶下缘压应力都有所减小，但减小幅度较小。当加固层为60cm时，拱脚下缘压应力较加固前减小17.5%，拱顶下缘压应力减小24.2%。拱脚、拱顶上缘压应力呈先减小后增大的趋势。拱脚上缘压应力的拐点出现在加固层厚度为30～40cm之间，拱顶上缘压应力的拐点出现在加固层厚度为0～10cm之间。

由此可见，加固层的部分自重由原拱圈承担，但随着加固层厚度的增加，原拱圈对加固层自重的承担越来越少，加固层受力凸显。

4.2 加固后原拱圈截面在活载作用下的应力

加固后原拱圈截面在活载作用下的应力如表2、图9所示。

表2 加固后原拱圈在活载作用下的应力值

通过表2、图9发现，加固后原拱圈在活载作用下拱脚、拱顶上下缘拉应力均有所减小，而且在加固层厚度小于20cm时，减小幅度较大，其中拱脚上缘减小趋势较其他位置平缓。加固层厚度在20～60cm之间时，减小的趋势较平缓，可见加固层很好地分担了活载的作用。当加固层厚度为20cm时，拱脚上缘、拱脚下缘、拱顶上缘、拱顶下缘的拉应力分别较加固前减小30.9%、81.8%、50.0%、82.0%。

图9 加固后原拱圈在活载作用下应力值与加固层厚度的关系

活载由复合拱圈承担，随着加固层厚度的增加，加固层对活载的承担越来越多，减小了原拱圈的受力。

4.3 加固后原拱圈截面在收缩徐变作用下的应力

加固后原拱圈截面在收缩徐变作用下的应力如表3、图10所示。

表3 加固后原拱圈在收缩徐变作用下的应力值

通过表3、图10发现，加固后原拱圈在收缩徐变作用下拱脚拱顶上缘、拱脚下缘压应力出现先增大后减小的趋势。拱脚下缘及拱顶上缘在加固层厚度为30cm时，截面压应力较加固层厚度为10cm时增大76.2%和77.1%。拱脚上缘在加固层厚度为20cm时，截面压应力较加固层为10cm时增大27.8%，而后随着加固层厚度的增加，压应力越来越小。拱顶下缘压应力随加固层厚度的增加持续增大，但增大趋势渐缓，当加固层厚度为30、60 cm时，截面压应力较加固层厚度为10cm时分别增大98%和123%。

图10 加固后原拱圈在收缩徐变作用下的应力值与加固层厚度的关系

从应力的变化可见，随着加固层厚度的增加，虚拟拉力越来越大，并且力的作用点离原拱圈下缘越来越远，从而使原拱圈受力形式从小偏心受压趋于大偏心受压。

4.4 加固后原拱圈截面的总应力

加固后原拱圈总应力如表4、图11所示。

表4 原拱圈在自重、活载、收缩徐变作用下的应力值

图11 原拱圈总应力与加固层厚度的关系

通过表4、图11发现，在加固前原拱圈拱顶下缘已出现0.62MPa的拉应力，当加固层厚度为10 cm时，拱顶下缘已经从受拉应力变为受0.59MPa的压应力。拱顶上下缘处的压应力随加固层厚度增大而增大，且当加固层厚度小于20cm时，增大幅度较大；加固层厚度在20～60cm之间时，压应力增大的趋势趋于平缓。当加固层厚度在0～30cm时，拱脚上下缘压应力急剧增大，加固层厚度在30～60 cm时，压应力有小幅减小的趋势。可见，当加固层厚度为20～30cm，即为原拱圈厚度的0.31～0.46倍时，各截面压应力增大明显，加固效果明显。

原拱圈各截面的压应力都会随着加固层厚度增大而增大，压应力储备也会有所增加，当加固层厚度小于原拱圈厚度的0.31～0.46倍，各截面压应力增加明显；当大于此厚度时，压应力增大趋势越来越少，甚至出现压应力减小的情况。