基于收敛-约束法和ZSI的隧道初期支护时机研究

2020-09-07张子龙姜谙男吴洪涛焦明伟

公路工程 2020年4期

张子龙，姜谙男，吴洪涛，焦明伟

（1.大连海事大学交通运输工程学院，辽宁大连 116026；2.吉林省交通规划设计研究院，吉林长春 130021）

0 引言

新奥法是现代隧道施工理念的重要标志，目前已得到广泛应用。其核心的锚喷支护强调柔性支护与围岩共同变形、最大可能利用围岩承载能力。在围岩与支护相互作用的过程中，若过早施作支护结构，围岩应力得不到有效释放，支护结构承受大部分原岩应力，需要较大的支护刚度；反之若支护时机过晚，洞周围岩产生有害的松动变形，影响施工安全。因此，隧道支护结构的设计应兼顾安全与经济双重指标，支护时机如何选择成为需要解决的重要问题。收敛-约束法是解决该问题的一种隧道稳定性分析方法［1］，该方法利用围岩特征曲线和支护特征曲线的相互关系，力求最大限度地发挥围岩的自承能力和付出尽可能少的支护代价，从而确定对应的支护时机［2］。但是收敛-约束法分析给出的最佳支护时机是围岩在稳定临界状态下的应力释放率，它是围岩表观的指标，不能直接反映围岩内在稳定程度，对于实际工程而言也缺乏指导意义，因此不能直接用来作为支护时机。

由空间效应原理可知，与掌子面不同距离处的隧道断面对应了不同的围岩应力释放率。将空间效应与收敛约束法相结合，即可得到支护与掌子面的控制间距。孙钧［3-4］等提出了虚拟支撑力法，引入了荷载释放系数的概念，使研究围岩应力释放的过程简化为二维问题。张传庆［5］等通过控制节点的不平衡力将应力释放法引入到了FLAC3D当中，并结合收敛-约束原理论述了应力释放法在隧洞工程中的应用。何满潮［6］等阐述了软岩巷道支护原理，提出了最佳支护时间和最佳支护时段的概念，以围岩最大限度地发挥塑性区承载能力但并未出现松动破坏作为最佳的支护时机选择。崔岚［7］等利用隧道纵向变形曲线与围岩特征曲线相互耦合，得出了开挖面附近某一位置处相应的虚拟支撑力。张妍珺［8］等基于收敛-约束法建立了开挖荷载释放率与支护距离之间的联系，对合理的初支时机进行了估算。杨灵［9］等采用数值模拟的方法分析了不同荷载释放率下围岩应力的变化，以围岩扰动区等效应力和屈服应力比值的大小初步确定了较为合理的初期支护时机。苏凯［10］等提出位移完成率的概念，以此确定了开挖荷载释放率与开挖面间距之间的关系，给出了最佳初次支护时机的选择方法。周烨［11］等以大断面黄土隧道实际工程为背景，结合有限元数值计算，以不同荷载释放率下围岩位移的变化特征确定了初期支护的施作时机。

目前隧道初期支护时机的确定方法大多是以围岩变形规律或围岩位移速率对支护时机进行估算，位移受测点位置和围岩刚度等影响较大，并且不能完全反映围岩内部破损情况。一般基于理想弹塑性模型的塑性区指标过于单一，无法量化，不能直观地反映围岩的安全或危险状态。因此，寻求更好的定量化局部稳定性评价指标作为位移判据的补充，是相当必要的。单元状态指标（Zone State Index，ZSI）是马春景［12］等在屈服接近度［13］和破坏接近度［14］的基础上进行变换和整合而提出的，实现了对围岩单元弹性、屈服和破坏3种应力状态的完整表达，可对围岩的安全或危险程度进行定量的描述。本文以甄峰岭2号隧道为工程背景，采用有限差分软件FLAC3D建立了二维和三维数值模型，分析了埋深和围岩级别对围岩特征曲线的影响，依据围岩特征曲线以围岩位移速率对最佳的支护时机所对应的应力释放率进行初步判定，并以围岩局部稳定性评价方法单元状态指标ZSI对计算结果进行验证，得出合理的计算结果。以相同的围岩位移作为出发点，对围岩特征曲线和纵向变形曲线耦合分析，建立起应力释放率和监测断面与掌子面间距之间的关系，确定支护与掌子面之间的控制距离，可为实际工程的施工提供指导和借鉴。

1 初次支护时机选择方法

1.1 收敛-约束原理

收敛-约束法的理论基础包含围岩特征曲线（Ground Response Curve，GRC）、支护特征曲线（Support Reaction Curve，SRC）和纵向变形曲线（Longitudinal Deformation Profile，LDP）。其中，围岩特征曲线和支护特征曲线反映了隧道开挖过程中围岩和支护结构之间相互制约的关系，如图1所示。其中，横坐标为隧道开挖后围岩的径向位移ur，纵坐标为支护结构所承担的径向围岩压力σr或支护反力Pi。

图1 围岩与支护相互作用关系示意图Figure 1 Relationship between surrounding rock and supporting structure

曲线①为隧道洞周某点的围岩特征曲线，分为弹性变形阶段（A点之前的直线段）、塑性变形阶段（AC段）、松动变形阶段（CD段）。曲线② ～④为支护特征曲线，反映支护结构的受力变形特征。两者的交点表示围岩与支护受力达到平衡，变形也不再继续发展。对比分析支护特征曲线②～④：曲线②在围岩变形处于弹性阶段时即施作支护，原岩应力未得到有效释放，支护结构承担较大的原岩压力，此时支护结构需要极大的支护刚度。反之，若支护结构施作过晚，洞周围岩已产生有害松动变形，所需的支护力反而有所增加，如曲线④。由此可知，围岩进入塑性屈服并不意味着已经完全失稳，隧道最佳的支护时机应允许围岩产生一定的塑性变形，但应控制其不产生过多的有害松动，曲线③即为较为理想的支护选择。

因此，隧道最佳支护时机的选择可以简化为在围岩特征曲线上确定一点（例如点B），该点处围岩已经最大限度地发挥了塑性区承载能力但并未出现松动破坏。这就需要对该点处围岩的稳定性进行分析，选择合理的稳定性评价方法是十分重要。

1.2 单元状态指标评价方法

单元状态指标ZSI是一种围岩的局部稳定性评价方法，它将岩土材料视为不同的单元，以ZSI值的大小表征围岩在弹性、屈服和破坏不同应力状态下的安全或危险程度。规定拉应力为负，压应力为正，且 σ3＜σ2＜σ1，ZSI推导过程如下：a.弹性阶段。

弹性阶段单元的破坏服从Mohr-Coulomb屈服准则，应力空间中的屈服面如图2所示。其中，P为应力空间中任意一点，坐标为（σπ，τπ）；O′为等倾线与π平面的交点，视为相对最安全的参考点，坐标为（σπ，0）；D点为O′P的延长线与BAC平面的交点，D点位于屈服面上，坐标为（σπ，τπ′）；点状线O′E位于 π平面上，与O′A垂直，则O′E与O′D的夹角等于应力罗德角 θσ。弹性阶段的单元不产生塑性应变，σ1≤0时不存在拉应力，单元以弹性剪切状态考虑，ZSI值按单元的实际应力状态点P进行计算。此时ZSI值等于应力空间中O′D与O′P的比值，表述为：空间应力点中相对最稳定参考点沿罗德角方向到屈服面的距离与该参考点和实际应力点间的距离的比值。

图2 应力空间上应力点状态Figure 2 Stress state of a point in stress space

I1为应力张量第一不变量，J2为偏应力张量第二不变量。具体推算过程如下：

点P位于屈服面上时，ZSI＝1。点P位于等倾线上时，ZSI＝＋∞，表示单元在弹性剪切状态下所能达到的最安全状态。

上述推算过程仅考虑了单元的弹性剪切状态，而岩土体的抗拉强度远小于其抗剪强度，因此拉伸状态下单元的安全性亦不容忽视，此时的ZSI＝σt／σ1。当 σ1接近于0时，ZSI值趋于无穷大，此时单元达到受拉状态下相对最安全的状态，但是仍不能排除发生剪切破坏的可能性。因此，弹性阶段ZSI取值为同时考虑剪切与拉伸破坏下的较小值，表达式为：

弹性阶段ZSI的取值为［1，＋∞），ZSI＝1时，单元进入屈服阶段；ZSI＞1时，单元处于弹性阶段，ZSI值越大安全程度越高。

b.屈服阶段和破坏阶段。

屈服和破坏阶段岩土体产生塑性变形，其等效塑性应变大于0。此时应用应变来来描述岩土体屈服和破坏的条件［15］，同时参考在文献［16］用剪应变与临界塑性剪应变的比值作为破坏度，将破坏临界点的等效塑性应变值 ¯εps为破坏的判据。εps／¯εps表示材料在剪切屈服段内距离破坏段的接近程度，其相补参量1-εps／¯εps作为剪切屈服状态的单元安全指标ZSI。εpt和¯εpt分别代表等效塑性拉伸应变和极限等效塑性拉伸应变。考虑拉伸情况的ZSI值取2种情况下的较小值，即：

屈服阶段ZSI的取值为［0，1），材料刚刚进入屈服段时，εps＝0，ZSI＝1。到达等效塑性应变阈值时，ZSI＝0。ZSI值越大单元安全程度相对越高。破坏阶段剪切与拉伸状态的ZSI表达式与屈服阶段相同，此时ZSI的取值为（-∞，0），ZSI值越小单元破坏程度越大。

围岩在不同应力状态下的ZSI值汇总如表1所示。

1.3 最佳支护时机选择方法

最佳支护时机的确定分为以下两步：对不同应力释放率下的围岩稳定性进行评价，给出基于应力释放率的最佳支护时机判定；将应力释放率应用于三维空间，最终给出基于支护与掌子面控制间距的最佳支护时机选择。

表1 围岩不同应力状态下的ZSI值Table 1 ZSI of surrounding rock under different stress state

采用二维数值模型和应力释放法［5］计算隧道在开挖完成后不同应力释放率（λ＝0～100%）下的应力和位移状态，绘制围岩特征曲线（GRC）。对各应力释放率下围岩的稳定性进行评价，确定出围岩在稳定临界状态下的应力释放率作为隧道最佳的支护时机。对围岩稳定性的评价分两步进行，首先以围岩位移速率作为稳定性评价指标对围岩在各应力释放率下的稳定性进行评价，对支护时机对应的应力释放率进行初步判断；其次，以围岩局部稳定性判断方法单元状态指标ZSI对围岩在不同应力释放率下的稳定性进行评价，对第一步计算结果进行验证，最终得出合适的应力释放率。

将应力释放率与空间效应相结合，计算隧道进行支护时与掌子面之间的距离。围岩纵向变形曲线（LDP）直观地展现了隧道开挖的空间效应，反应出与掌子面不同间距处隧道断面的位移，可利用三维数值计算得出。围岩特征曲线（GRC曲线）又反应了应力释放率与围岩位移之间的关系。由此可以利用相同的变量围岩位移，构建起LDP曲线和GRC曲线之间的对应关系见图3，将二维空间中的应力释放率对应至三维空间的中支护与掌子面的控制距离，使支护时机的选择更为直观，也可以为实际工程的施工提供借鉴。

图3 GRC曲线与LDP曲线对应关系Figure 3 Relationship between LDP and GRC

2 数值计算模型的建立

2.1 工程概况

甄峰岭2号隧道入口位于和龙市北部西城镇境内，出口位于安图县松江镇境内，属长白山系北侧，隧道分左右两幅，隧道间距32～40 m，右幅5 561 m，左幅5 497 m，属于特长隧道。隧道穿越甄峰岭北部山地之间，周围山峦连绵起伏，沟谷纵横，属于构造剥蚀低山地貌。隧道主体走向以北东向为主，主体围岩分级涵盖Ⅲ～Ⅴ级围岩，隧道最大埋深近400 m。隧道区在大地构造上位于中朝准地台的IV级构造单元与和龙地块北部边缘带接触，其北侧为古洞河北西向深大断裂带。隧道通过的地区岩性主要为新太古代甲山岩组：岩性为变质英云闪长岩、新生代船底山组：玄武岩。上覆第四系松散层。

2.2 数值计算模型

采用FLAC3D有限差分软件建立二维和三维数值模型，为了消除边界效应的影响，左右边界和下边界取隧道3倍洞径以上，上边界竖直向上取至地表，二维模型深度方向取单位长度1 m，三维模型深度方向取100 m，隧道横断面按设计取用。模型尺寸分别为92 m×99 m×1 m和92 m×99 m×100 m，如图4所示。模型底部边界设置固定约束，四周边界设置法向约束，上部边界为自由面。计算模型采用应变软化模型，软化参数的取值方法参考文献［12］，围岩的物理力学参数取值如下表2所示。

表2 围岩物理力学参数Table 2 Physico-mechanical parameters of surrounding rock

2.3 计算方案

隧道主体部分涵盖Ⅲ～Ⅴ级围岩，埋深跨度亦较广。Ⅴ级围岩段由于岩体本身的物理力学性能较差，实际施工中一般采用多种超前支护措施来保障施工安全，支护时机的问题不予讨论。因此，本文主要针对Ⅲ、IV级围岩条件下隧道结构的稳定性进行计算，同时依据埋深的不同，分为以下4组工况进行分析，见表3所示。

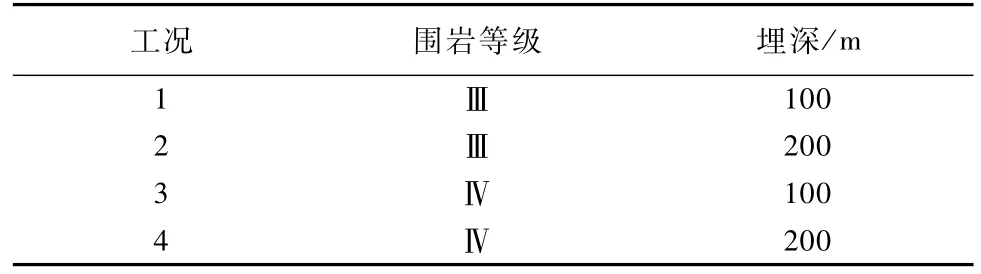
表3 工况定义Table 3 Case definition

3 计算结果分析

3.1 不同应力释放率的围岩位移速率分析

利用FLAC3D内置的Fish语言，在开挖后的隧道洞周节点添加不同大小（λ＝0～100%）的虚拟支撑力来模拟围岩应力逐渐释放的过程，计算得到不同应力释放率下的围岩位移值，从而得出围岩特征曲线，结果见图5。对比工况1、3或工况2、4可知，相同埋深下，围岩性质越好，其围岩特征曲线越接近于直线，曲线的斜率变化较小；反之，围岩性质较差，围岩特征曲线为发散状，曲线斜率变化较为明显。对比工况1、2或工况3、4可知，相同围岩级别，埋深和地应力水平的增大，围岩特征曲线的斜率变化较大，相同变形量所对应的围岩支护力有较大程度的增加。围岩性质越差或埋深越大，围岩特征曲线的曲线段长度越长，同时曲线斜率也呈单调递增的趋势。

图5 各工况下围岩特征曲线Figure 5 Ground response curve under different conditions

图6 各工况下围岩洞周节点位移增量Figure 6 Displacement increment of surrounding rock under different conditions

以洞周围岩的位移速率作为支护时机判断依据的方法认为：隧道开挖完成后，围岩应力释放的初期阶段围岩位移近似线性变化，而当应力释放程度达到某一值后围岩位移会出现突增点，则此点所对应的应力释放率则作为最佳支护时机的参考［8］。以工况1和工况4为例，图6给出了其围岩洞周监测点位移增量的变化情况。工况1为Ⅲ级围岩和较浅的埋深，对应的在应力释放率达到80%时洞周围岩位移增量出现陡增，则认为此时岩体进入明显塑性屈服阶段，宜采取支护措施。而工况4为Ⅳ级围岩且埋深较大，在应力释放率为50%时洞周围岩位移增量已出现陡增。以此得出各工况下隧道的最佳支护时机所对应的应力释放率分别为80%、

60%、50%、50%。

3.2 不同应力释放率的围岩ZSI分析

单元状态指标ZSI的评价方法可以依据ZSI值的大小直观的反映围岩所处的应力状态，并对围岩的安全或危险程度进行评价。依据1.2节对于单元状态指标ZSI的理论推导，利用FLAC3D内置的Fish语言进行二次开发，实现了在FLAC3D中对ZSI的计算。对隧道开挖完成后洞周围岩在不同应力释放率下ZSI值进行计算，分析各状态下的围岩稳定性，给出隧道最佳支护时机所对应的应力释放率。以工况4为例进行分析，计算结果如图7所示。

分析可知，λ＝20%时，地应力是引起洞周围岩内力变化的主要因素，隧道拱脚处出现应力集中，此时洞周围岩的破坏区（ZSI＜0）和屈服区（0＜ZSI＜1）主要分布在拱脚位置，拱腰处围岩均处于弹性状态（ZSI＞1），围岩整体稳定性较好。随着围岩应力释放程度的增加（λ＝40%），屈服区从拱脚向拱腰延伸，破坏区仍集中在拱脚处，起拱线以上围岩屈服区较小，未产生破坏区域，此时洞周围岩大部分区域仍处于弹性状态，不宜进行支护。当λ＝50%时，拱腰处围岩的屈服区进一步向深部扩展，同时破坏区开始出现，拱脚和拱腰处围岩的屈服区实现贯通，破坏区亦接近贯通，起拱线以上已有大部分屈服区和部分破坏区。此时拱腰处已存在安全隐患，宜及时进行支护。当λ＝60%时，围岩的屈服区已覆盖整个拱顶，破坏区在拱腰处进一步向深部发展并向拱顶延伸，起拱线以上已出现大面积破坏区域，洞周围岩完全进入塑性屈服，此时进行支护可能存在围岩松动脱落，有较大的安全隐患。当应力进一步释放（λ＝80%），屈服区和破坏区不断向围岩深部发展，破坏区也进一步向拱顶延伸，当应力完全释放时（λ＝100%），破坏区已经基本覆盖拱顶。根据以上分析可知，在λ介于40%和50%之间时进行支护最为合理，这与上文计算结果λ＝50%保持一致。

图7 不同应力释放率下单元状态指标Figure 7 Zone state index under different stress release rates

3.3 基于LDP和GRC耦合的支护时机确定

LDP曲线反映了距离开挖面一定距离处隧道洞周围岩的变形情况。在FLAC3D三维数值模型中，对隧道进行分步循环开挖，每步开挖1 m，记录各步开挖完成后掌子面与监测断面的间距及监测断面洞周节点的位移，以此建立围岩位移与开挖面间距之间的关系曲线，即LDP曲线。GRC曲线在3.1中已进行了相关计算。以隧道开挖后最危险位置拱顶位移作为同一因变量，将LDP曲线和GRC曲线建立在同一坐标系中进行耦合分析，构建起应力释放率和隧道某一断面与掌子面距离之间的关系，给出基于支护与掌子面的控制距离的支护时机选择。仍以工况1和工况4为例进行二维和三维数值计算，耦合分析结果如图8所示。图中横坐标表示隧道开挖后围岩的拱顶位移；左侧纵坐标代表隧道监测断面与掌子面之间的距离，坐标为正表示位于掌子面后方，负表示位于掌子面前方；右侧纵坐标表示围岩的应力释放率。

图8 LDP与GRC耦合曲线Figure 8 Coupling curve of LDP and GRC

分析可知，工况1计算所得的最佳支护时机所对应的应力释放率为80%，此时的拱顶位移所对应的隧道断面位于掌子面后方4.6 m，则工况1下隧道最佳的支护时机滞后于掌子面4.6 m开始施作。同理，工况4计算所得的支护时机所对应的应力释放率为50%，此时的拱顶位移所对应的隧道断面位于掌子面前方1.9 m，因此工况4应超前掌子面1.9 m进行支护。由此计算得出各工况下开始施作支护时与掌子面之间的间距分别为4.6、1.6、-1、-1.9 m。则各工况下最佳支护时机施作时分别为滞后掌子面4.6、1.6 m，超前支护1、1.9 m，计算所得结果符合实际工程规律。