数控加工过程中缺陷振动仿真

杨亚楠 朱春华 刘春东 马立勇* 王久强 刘向辉 孙佳悦 马晓明

(1.河北建筑工程学院，河北张家口，075000；2.领克汽车张家口工厂，河北张家口，075000)

0 引 言

数控加工过程中，无论工件表面缺陷，还是电机缺陷，均会引起刀具与工件之间的相对振动[1].影响加工过程中振动的因素较多，因此振动过程的振幅、频率、相位角及振幅的增衰等参数一般不可控，目前国内的减振刀杆还无法完全将其消除[2].有研究表明，3.5×106ms内刀-件间便有可能会产生300万次振动(即850 Hz左右，此数据仅为文献[3]中实验所得，并非一般性规律).若工件表面有类似图1中的缺陷，其引起加工过程中垂直于机床方向的振动如图2所示[3].对于机械加工来说，刀-件之间的相对振动是引起表面形貌不平整的重要因素[4].因此研究工件、电机缺陷引起的振动意义深远.本文将利用小波包算法对加工过程中的振动进行计算，并基于ANSYS仿真模拟软件分别对加工过程中工件表面缺陷、电机缺陷引起的振动进行仿真计算，并利用现有数据进行对比分析.

图1 待加工缺陷工件 图2 缺陷工件引起垂直于机床方向的振动

1 小波包振动计算

1.1 算法简介

为了改善傅里叶变换在实际应用中的局限性，在其基础上进行小波变换，虽然更加抽象，但是有着处理能力更强，时频域范围更广等显著优点.

1.2 算法及分析

小波包算法是一种信号分析方法，特点是将较难计算的高频信号分成更多的小频段，因此其计算结果更加精准[5].其频段自适应的特点也可以大大提高计算的分辨率.首先有多分辨模型：

(1)

其中，L2(R)为可积空间域；Wj是函数的子集.

将多辨函数进行空间分解，可以得到不同尺度集下的空间子向量.这些不同频段下的空间子向量正交之和即为函数本身，此时高频段的分辨率达到最大，有：

(2)

(3)

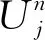
(4)

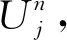
(5)

(6)

式中，gk=(-1)kh(1-k)，两系数空间相乘为0.

当l=0时，有：

(7)

(8)

将一阶函数u0(x)与二阶函数u1(x)分别进行退化计算，即可得到尺度函数φ(t)与小波函数ψ(x).

1.3 算法实现

正交分解小波包的使用范围很广，任何信号内的所有频域均可以对其计算.算法的步骤是先进行分解，然后分别对任意高频低频部分进行二次抽值计算，只存储奇数位或偶数位的数据.最后继续对其子信号进行分解、抽值、存储.分解的级数越高，频域段的拟合更加细腻，所得到的信号分辨率也相应地更高.所以有小波包分解及重构的公式为：

(9)

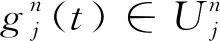
根据该式得小波包分解算法：

(10)

(11)

式中，ak-2i和bk-2i为求解小波包函数所需的滤波系数.

得到重构的小波函数：

(12)

2 基于ANSYS缺陷振动仿真分析

2.1 加工过程中工件表面缺陷振动

仿真需要利用三维绘图软件UG进行工件模型的绘制，为了使模型在导入ANSYS前便有较好的网格划分，要以X_T接口导出模型.导入到ANSYS中的模型需要进行前处理(材料属性设置、约束设置以及网格划分等)为了提高计算精度设置网格245175个，有节点462153个，划分结果如图3所示.已经有文献实测出铣削“S”试件铣削力，本文直接以载荷的方式施加到三维模型上[6].

图3 工件表面网格划分 图4 试件六阶固有频率

材料设置为铝合金6160，因此求得该工件的六阶固有频率如图4所示.求振动情况前，需要先对加工“S”试件过程中变形进行求解(本次仿真认为刀具为刚性).变形结果如图5所示.

a)等效变形 b)工件的总变形

在已知工件变形的情况下，结合刀具加工轨迹(刀具轨迹为摆线，但是利用微元法可以将其简化为圆弧)即可求得三个方向的振动情况，如图6所示.

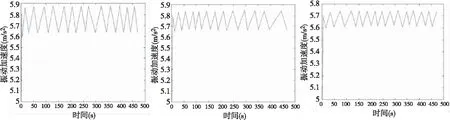
a)x方向 b)y方向 c)z方向

2.2 加工过程中伺服电机缺陷振动

机床伺服电机转动时，若电机内出现磨损等不良现象便会引起动不平衡，进而加剧加工过程中正常产生的振动.仿真方法同2.1，为了简化计算，不对电机不同位置进行单独材料设置，均设置为结构钢.建模步骤同样为：三维建模、接口导入、划分网格，划分结果如图7所示.

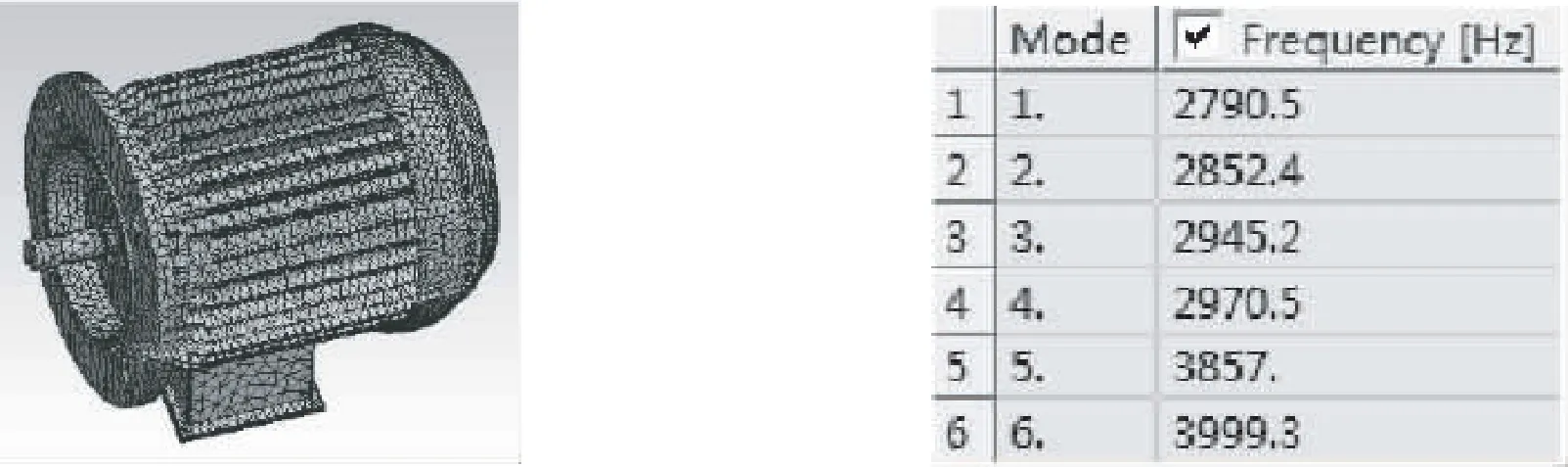
图7 电机网格 图8 缺陷伺服电机固有频率

图中共有单元：321564个单元；节点：526573个.得到其固有频率，如图8所示.其三个方向振动仿真结果如图9所示.

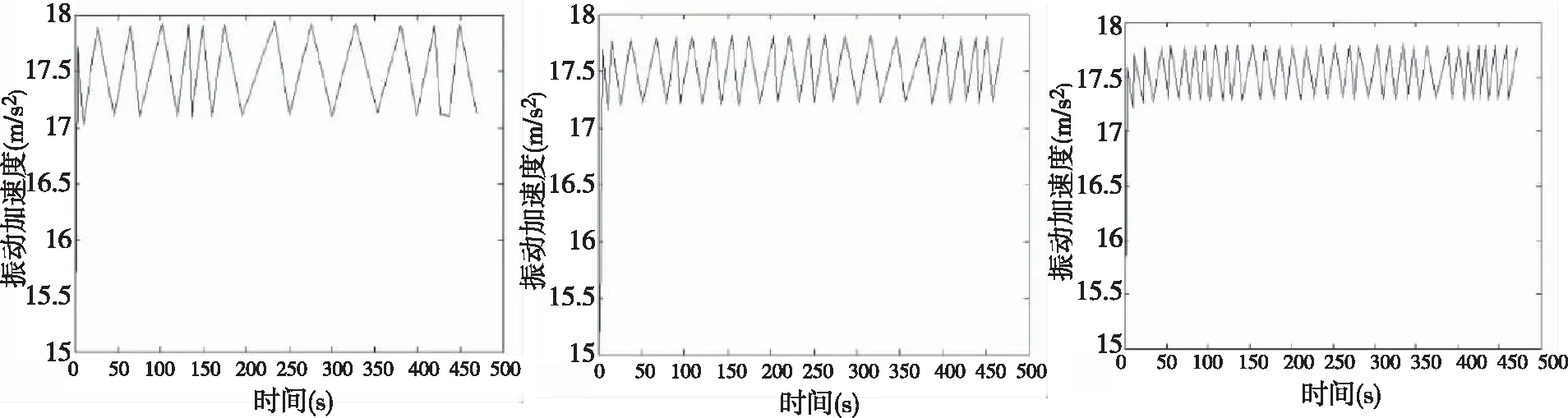
a)x方向 b)y方向 c)z方向

3 总 结

首先对傅里叶变换进行优化，得到小波包变换算法，以得到满足考虑缺陷的计算模型.然后分别对有缺陷的工件表面、动不平衡的电机进行振动仿真分析(对其中一个对象进行仿真时，认为另一个为刚性不产生振动，若想要得到两个缺陷同时存在的振动结果可用叠加原理进行计算求解).由文献[1]可知，振动加速度越大，越会对加工产生不利影响(非线性关系)，通过对比两种缺陷的振动加速度不难看出，电机振动缺陷明显大于工件.通过工件加工缺陷的实验与仿真结果对比分析，可以得知仿真方法符合实际.因此，可以判断电机的仿真结果应与实际相符，为今后如何控制振动奠定基础.