带冲突约束两台平行专用机排序的一个改进算法
2022-06-08陈光亭
张 亮,张 安,陈 永,陈光亭
(1.杭州电子科技大学理学院,浙江 杭州 310018;2.台州学院电子与信息工程学院,浙江 台州 318000)
0 引 言
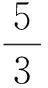
1 问题描述
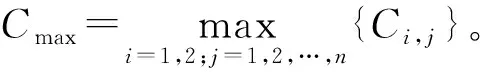
本文研究的是PD2conflict,seq1Cmax问题的一种特殊情形,即各个工件的加工时间需满足
min{p1,1,p1,2,…,p1,n1}≥max{p2,1,p2,2,…,p2,n2}
(1)
Hong等[4]已经证明该情形是强NP-难。
2 算法设计与分析
对于满足式(1)假设的PD2conflict,seq1Cmax问题,文献[5]提出一种基于工件加工时间非增顺序(Largest Processing Time first,LPT)规则的近似算法,简称LPT算法,主要步骤如下。
(1)将J1中的工件按给定的次序从零时刻开始无空闲地在M1上加工,直至完工。
(2)将J2中的工件按照加工时间非减次序排列。
(3)对J1中任意一个工件J1,j,其加工时间窗口为[S1,j,S1,j+p1,j]。从j=1到j=n1,在J2的序列中挑选出当前尚未加工且与J1,j不冲突的工件,在M2上的时间窗口[S1,j,S1,j+p1,j]内无空闲地加工该工件,除非该工件的完工时间超出上述时间窗口。
(4)若J2中仍有未加工的工件,则从S1,n1+p1,n1时刻开始,在M2上无空闲地加工这些工件,否则结束算法。
(1)令S1,1=0,即将工件J1,1安排在M1的零时刻加工。

(3)若J2中仍有未加工的工件,则在J1,n1的时间窗口中的最后一个工件的完工时,开始在M2上无空闲地加工这些工件,否则结束算法。


证明在J1,n1完工时间之后,才开始加工的那部分工件的集合,记为B5,B5可以为空集;J1中,在其时间窗口内,M2上工件加工时间之和不小于自身加工时间的工件的集合记为A1;J1/A1中,与B5中所有工件均冲突的工件的集合记为A4;J1/(A1∪A4)中,在其加工窗口内,M2上只加工专属工件的工件的集合记为A3;记A2=J1/(A1∪A3∪A4)。在A1,A2,A3,A4中,工件的时间窗口内,M2上加工的工件集合分别记为B1,B2,B3,B4。MLPT算法所得排序类型如图1所示。

图1 MLPT算法所得排序类型

根据MLPT算法步骤,算法所得排序的最大完工时间可以表示为:
(2)
由A1,B1的定义及MLPT算法的步骤2,可知
(3)
显然,有
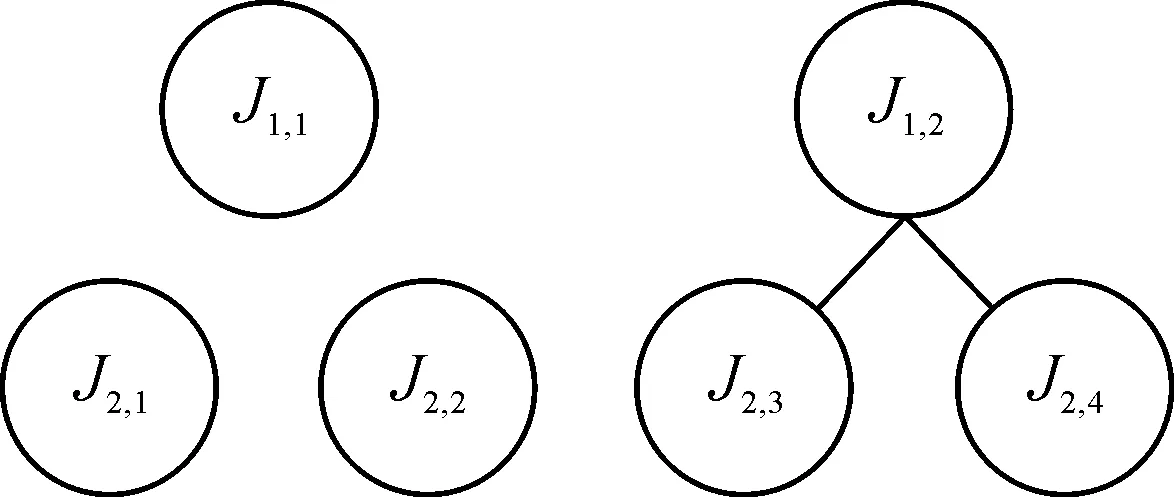
0≤b4 (4) 最优排序需加工完J1和J2中的所有工件,又由于A4和B5的冲突关系,最优排序中这两个集合中的工件的加工时间窗口不允许重叠,则最优排序的最大完工时间需满足: (5) (6) 图2 J1,x时间窗口内加工情况 (7) 图3 J1,y时间窗口内加工情况 由a1,a2,a3和T1间的大小关系,MLPT算法的近似比分析分为以下两种情形。 由式(2)、式(3)、式(5)可知, (8) 由式(6)、式(7)可知, (9) 由式(2)、式(5)和式(9)可知, (10) 专用机M1和M2分别加工工件集J1={J1,1,J1,2}和J2={J2,1,J2,2,J2,3,J2,4},M1上工件的加工顺序为J1,1,J1,2。各工件的加工时间如表1所示,冲突图如图4所示。 表1 实例中各工件的加工时间表 图4 实例的冲突图 图5 加工实例的排序结果

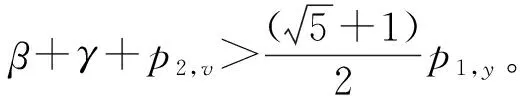




3 算法紧例



4 结束语

