铁尾矿砂浮石混凝土梁抗剪性能数值模拟研究
2020-09-07曹传海翁维素马晨洋孙晓涵郭洪礼潘宏宾
曹传海 翁维素 马晨洋 孙晓涵 郭洪礼 潘宏宾 杨 宁
(河北建筑工程学院,河北省土木工程诊断、改造与抗灾重点实验室,河北 张家口 075000)
0 引 言
轻骨料混凝土是用轻粗骨料、普通砂或轻细骨料、胶凝材料和水配制而干表观密度不大于1950 kg/m3的混凝土[1].本文研究的是以40%的铁尾矿砂代替天然砂,浮石作为粗骨料的铁尾矿砂浮石混凝土.近些年以来,国内外对于铁尾矿砂混凝土和浮石混凝土的研究越来越多,高旭[2]等对铁尾矿砂浮石混凝土的基本力学性能进行了研究,得到了混凝土的基本的力学性能参数以及基准配合比.本文通过数值模拟的方法,找到最适合铁尾矿砂浮石混凝土的塑性本构关系计算方法,并对铁尾矿砂浮石混凝土梁的抗剪性能进行数值模拟,为后续的研究提供经验.
1 有限元模型
本次研究通过建立11个轻骨料混凝土梁模型,对其混凝土强度等级、剪跨比以及配箍率的不同来研究铁尾矿砂浮石混凝土梁的抗剪性能.构件梁的尺寸150 mm×300 mm×2200 mm,钢筋采用HRB400级钢筋,直径分别为6 mm、10 mm和22 mm.模型分为三组:(1)混凝土等级为LC25、LC30、LC35;(2)剪跨比分别为0.5、1、1.5、2、3、3.5;(3)配箍率分别为0.76%、0.38%、0.253%、0.19%.
1.1 模型建立
部件(Part)采用分离式建模,混凝土梁采用C3D8R积分单元.箍筋和纵筋采用Truss单元.模型建完如图1所示,以LC30为例.

图1 模型示意图
1.2 分析步和相互作用
ABAQUS有多种的分析部以适应不同的加载形式,本次试验模拟采用静力通用(Static,General),一共分为2个分析步,分别为接触荷载和受力荷载.本次模型钢筋采用嵌入区域约束(Embedded Region)形式约束到混凝土模型里.垫块和混凝土之间采用绑定(Tie)约束,垫块和混凝土之间没有相对运动.模型施加位移时,在垫块上方建立一个参考点,并将参考点和垫块上表面通过耦合(Coupling)作用在一起,把位移施加在参考点上,通过参考点传递到垫块上.
1.3 荷载和网格划分
混凝土梁模型的荷载施加采用位移加载,加载位置为两点对称分级加载.混凝土的边界条件一边支座为固定支座,另一端为铰支座.
有限元软件模拟分析时,单元的类型和单元的网格的大小对模拟精度、模拟时间以及模型的收敛起到了很重要的影响,综合考虑和多次试验模拟以后,选择网格宽度为50 mm来布置全局种子.
2 材料的本构关系
2.1 钢筋的本构关系
本次模拟中,钢筋均采用HRB400级钢筋,其应力-应变关系采用双线性强化模型,根据实验测得的基本力学性能见表1.

表1 钢筋基本力学性能
2.2 轻骨料混凝土的塑性损伤本构关系
铁尾矿砂浮石混凝土的基本力学性能的试验的结果如表2所示.

表2 混凝土基本力学性能
铁尾矿砂浮石混凝土的塑性损伤本构关系还没有一个准确的公式,在翻阅了大量的文献以后,总结出国内轻骨料混凝土的本构关系大致有两种算法.第一种采用《混凝土结构设计规程》GB 50010-2010[3]里的全曲线方程,并采用里面的参数,公式如式(1)、(2)所示;王振宇[4]等采用的公式如式(3)所示,参数采用文献里的参数进行模拟.第二种是丁发兴[5]等提出的轻骨料混凝土本构关系,公式如式(4)所示.
σ=(1-dc)Ecε
式(1)
式(2)
式(3)
式(4)
从图中可知,不同计算方法的本构关系的上升段和试验值的结果相差不大,而下降段的差距相差很大,丁发兴提出的计算方法比王振宇和规范提出的计算方法相同荷载下应变值更大.对于同一个计算方法,参数的不同导致的下降段的曲线也相差很大,王振宇给出的参数算出来的应变比规范给出的参数要小很多.
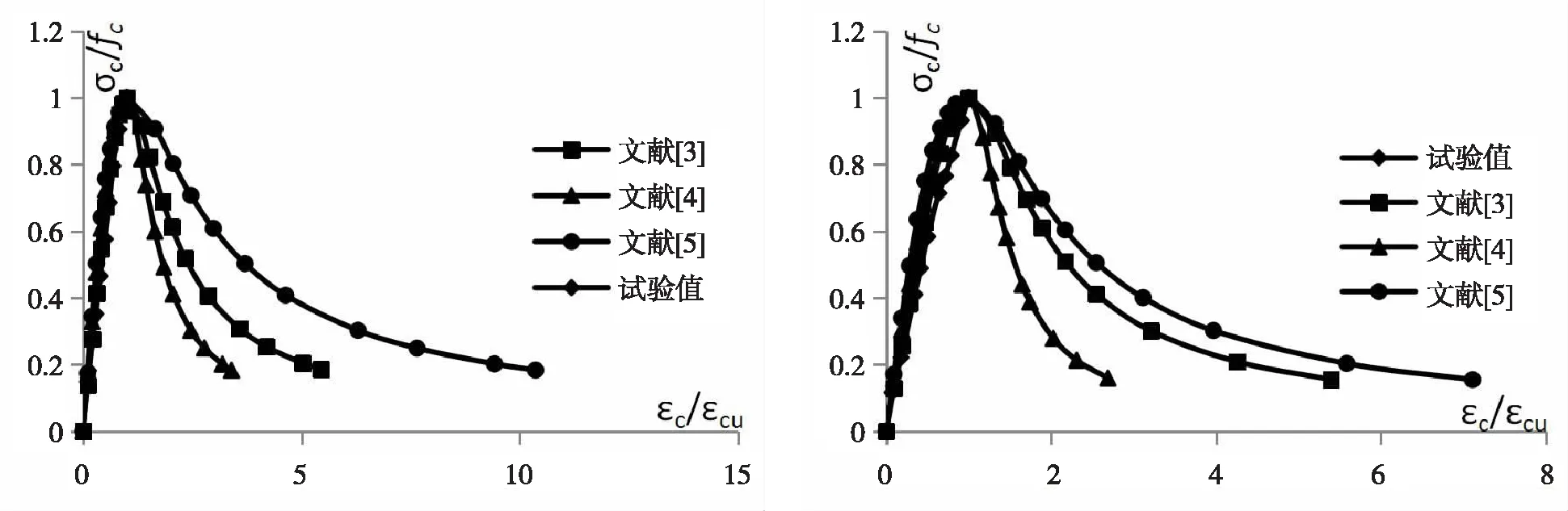
图2 LC25受压应力-应变关系对比 图3 LC30受压应力-应变关系对比
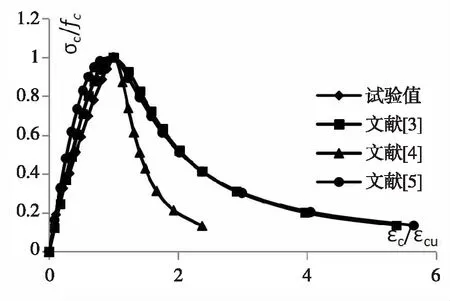
图4 LC35受压应力-应变关系对比
ABAQUS有很多本构模型,其中塑性损伤本构可以很好的模拟混凝土的破坏损伤,对于损伤因子的计算,现在国内关于混凝土损伤因子的计算有以下4种情况,分别为曾宇[6]等、杨飞[7]等、张劲[8]等、李伟琛[9]等提出的4种计算方法,其计算公式见式(5)-(8)所示.
式(5)
式(6)
式(7)
式(8)
以上公式中D为《混凝土结构设计规范》GB 50010-2010中的损伤演化系数,εc~in为非弹性应变,γ为非弹性应变与极限应变的比值.LC25-LC35的应变-塑性损伤因子曲线图见图5-图7所示.
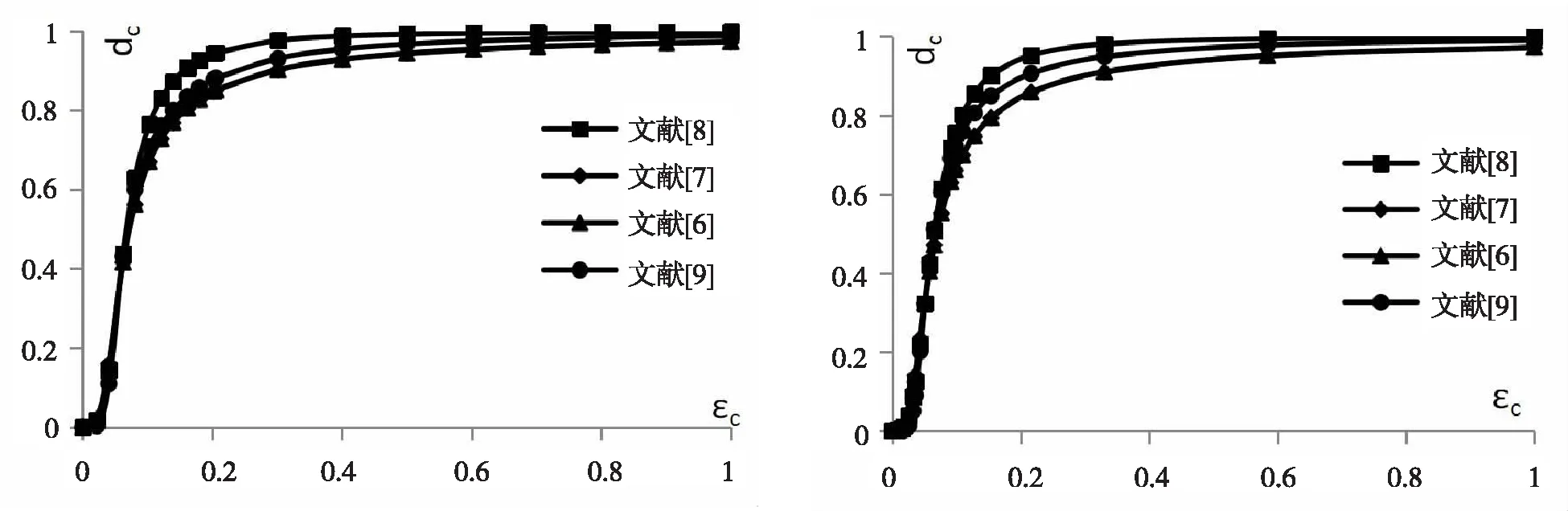
图5 LC25受压损伤因子-应变关系 图6 LC30受压损伤因子-应变关系
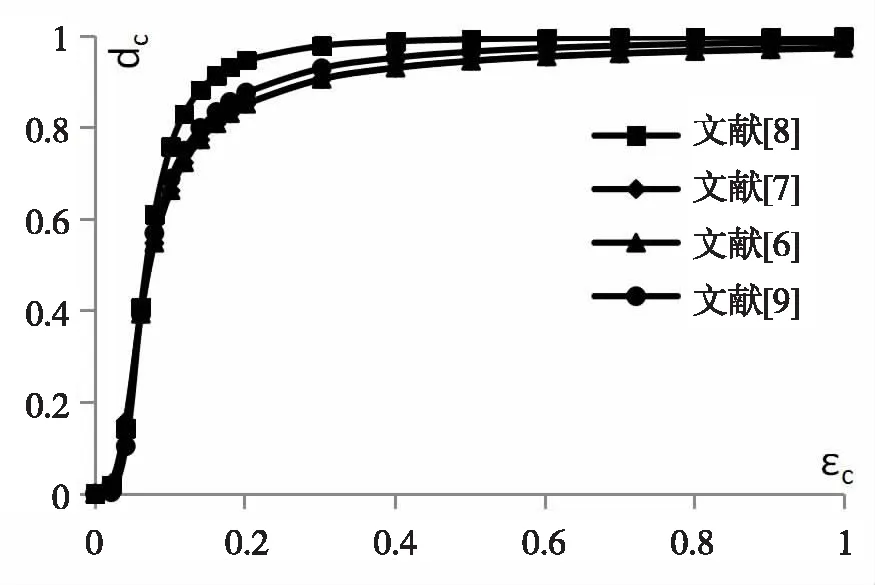
图7 LC35受压损伤因子-应变关系
从图上可以看出,张劲提出的损伤因子的算法比其他人的都大一点,混凝土抗剪模拟出来的荷载值相对的更小.李伟琛的算出来的损伤因子在比曾宇和杨飞算出来的结果大一点,但混凝土抗剪模拟出来的值与试验值差别很大.杨飞和曾宇给出的损伤因子计算方法计算出来的结果相差不大.
不同的塑性损伤本构关系,在其他条件相同的情况下,对铁尾矿砂浮石混凝土等级为LC25,LC30,LC35的梁进行模拟,其荷载-挠度结果见表3,表4所示.
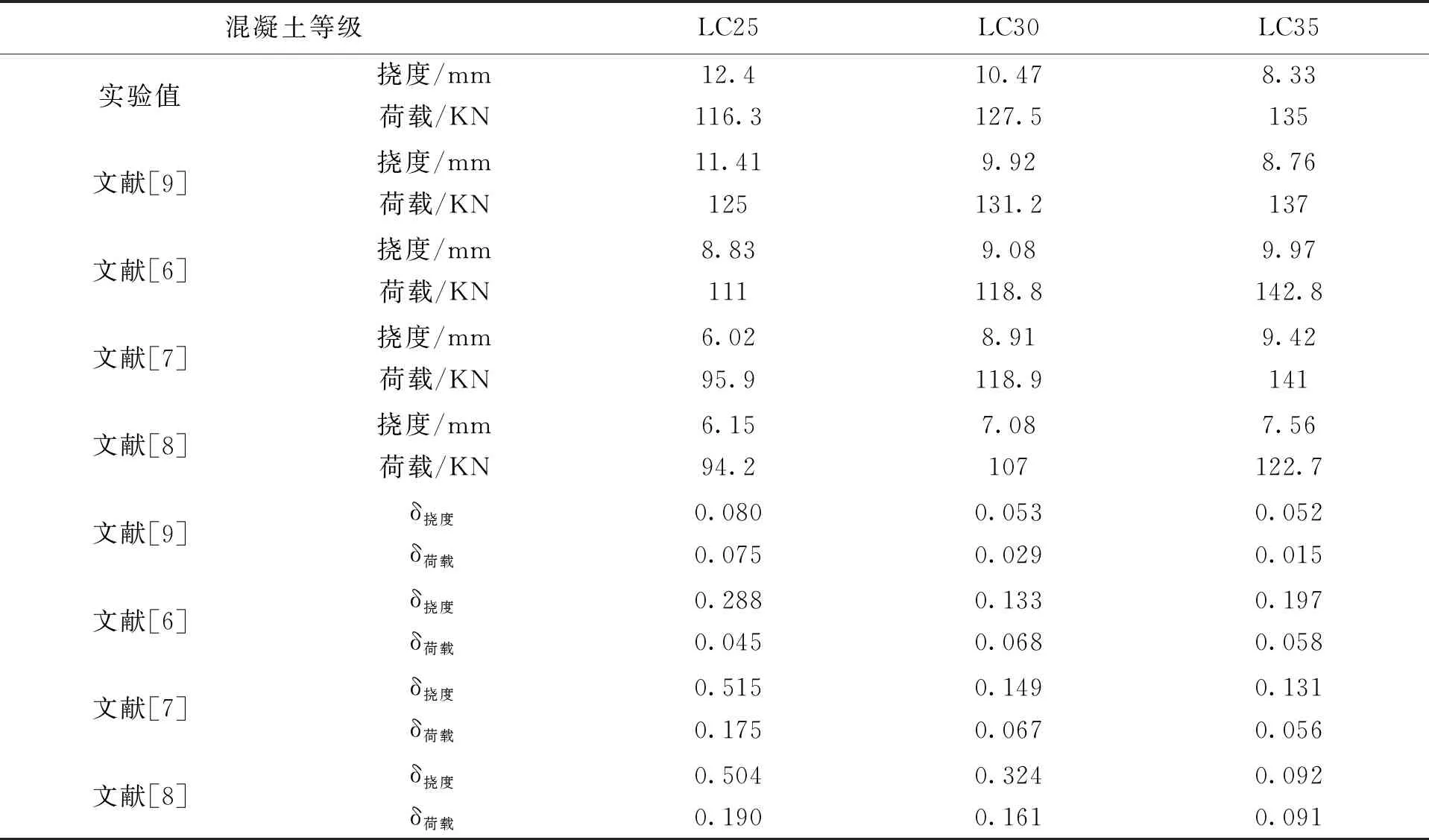
表3 损伤因子不同模拟结果
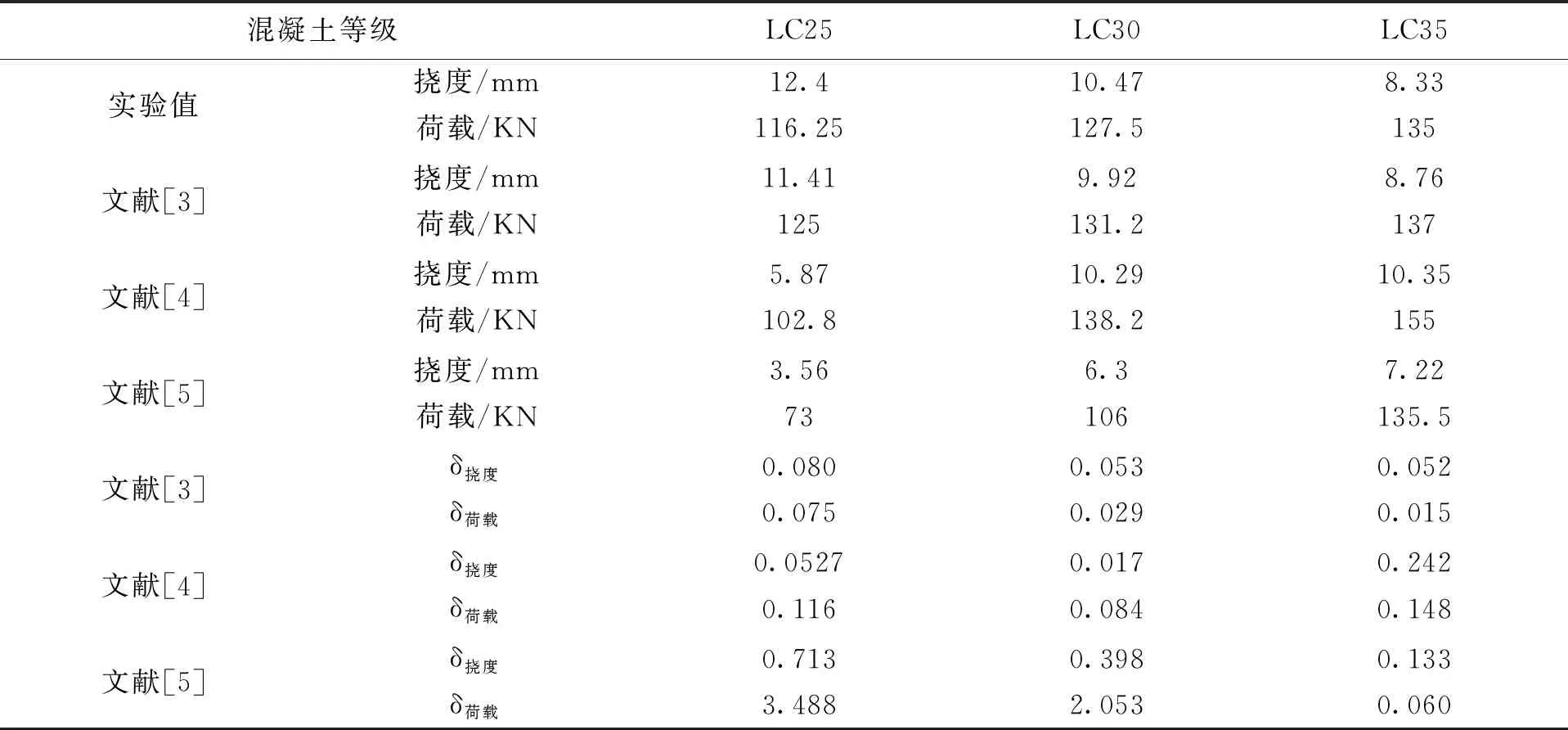
表4 本构关系不同模拟结果
通过数据处理,与试验结果进行对比,可以发现《混凝土结构设计规范》GB50010-2010里给的全曲线方程,对于铁尾矿砂浮石混凝土时最符合的,误差在10%以内,损伤因子则采用李伟琛提出的计算公式,误差在8%以内.最后采用的本构关系见图8-图9所示.
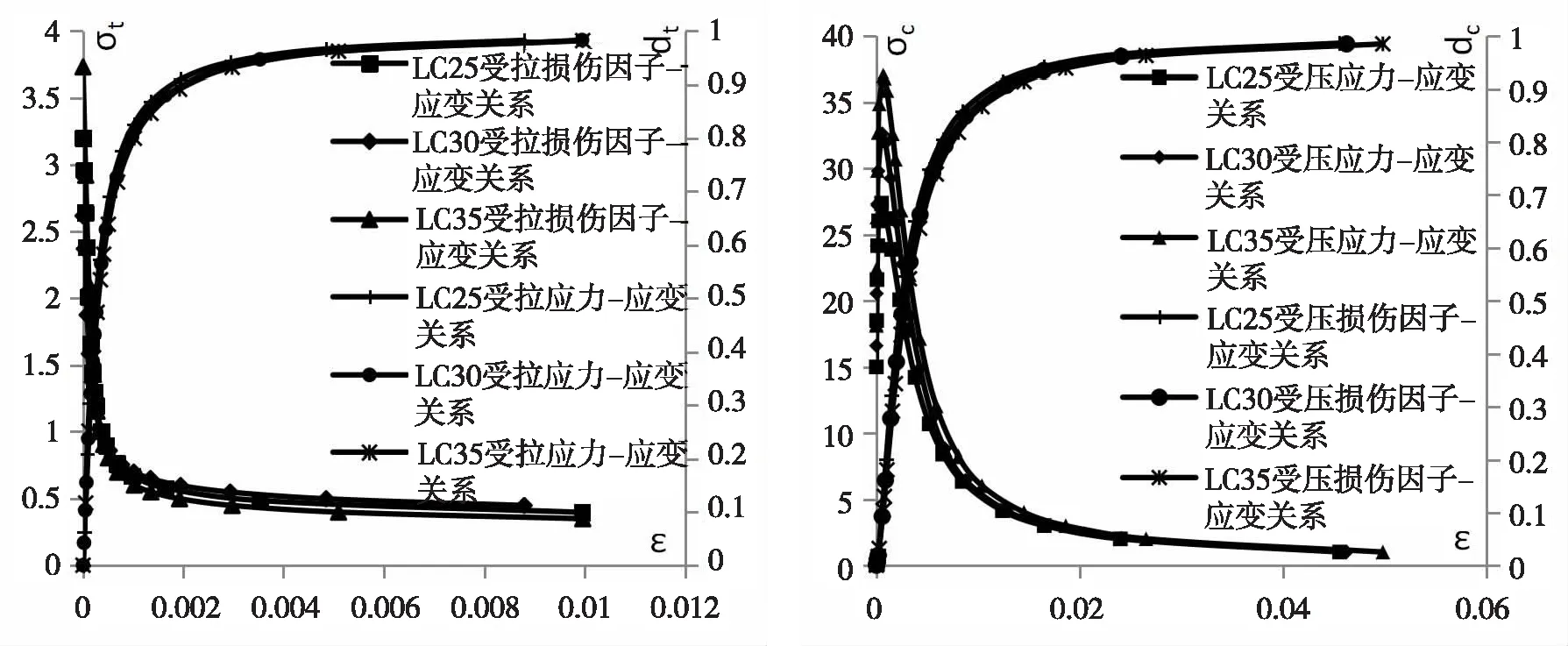
图8 受拉塑性损伤本构关系 图9 受压塑性损伤本构关系
3 有限元模拟结果及分析
3.1 剪跨比不同时的模拟结果
剪跨比是反映梁斜截面受剪承载力变化规律和区分发生各种剪切破坏的重要参数,它对再生混凝土受剪承载力的影响起到了主要作用.剪跨比为0.5、2.0、3.5的应力以及等效应变模拟结果图见图10-图12.不同的剪跨比模拟荷载-跨中挠度关系见图13,不同的剪跨比试验和模拟结果极限荷载和挠度见表5.
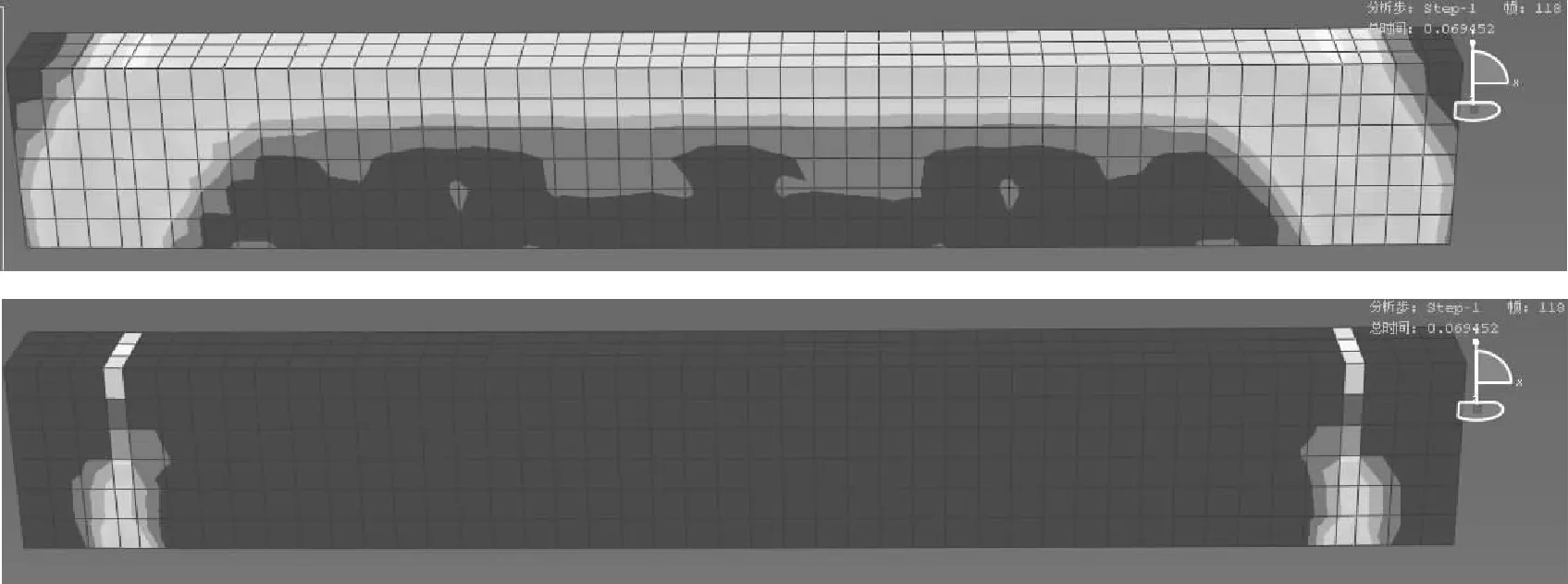
图10 剪跨比0.5应力及应变模拟图
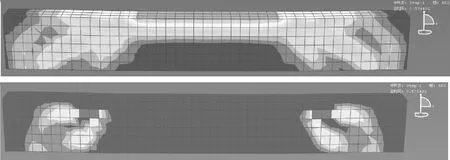
图11 剪跨比2.0应力及应变模拟图
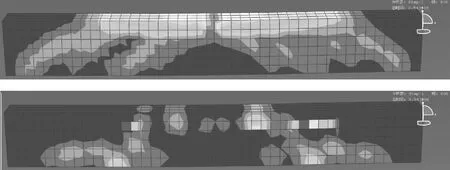
图12 剪跨比3.5应力及应变模拟图

图13 剪跨比不同荷载-跨中挠度关系
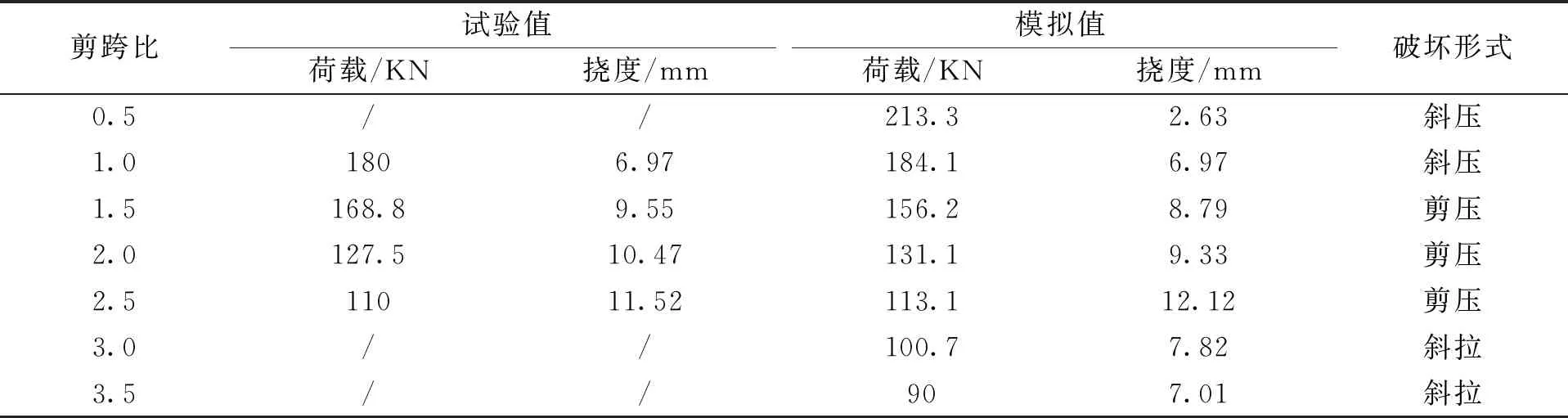
表5 剪跨比不同时试验和模拟结果
从以上的图表可知:剪跨比小于1.0时混凝土梁为斜压破坏,剪跨比大于1.0小于2.5时混凝土梁为剪压破坏,剪跨比大于2.5时混凝土梁为斜拉破坏.随着剪跨比的增大,混凝土梁的抗剪承载力越来越小.斜压和剪压破坏时,随着剪跨比的增大,跨中挠度越来越大.斜拉破坏不仅承载力减小,跨中挠度也随之减小.
3.2 配箍率不同时的模拟结果
配箍率为0.38%的钢筋应变图见图14,配箍率为0.19%的钢筋应变图见图15,配箍率不同时荷载-跨中挠度关系见图16,试验和模拟值得极限荷载和挠度值见表6.

图14 配箍率为0.38%钢筋应变图

图15 配箍率为0.19%钢筋应变图
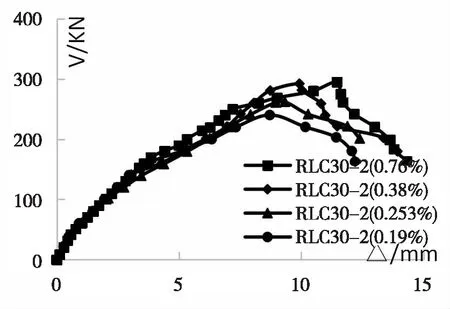
图16 配箍率不同荷载-跨中挠度关系

表6 配箍率不同时试验和模拟结果
从以上图表可知:配箍率大于0.38%时,混凝土梁的抗剪承载力没有很大的变化.配箍率在0.19%-0.38%之间,随着配箍率的增大,承载力变小了.随着配箍率的增大,跨中挠度不断减小.混凝土梁设计时,要选取合理的配箍率,不能超筋和少筋,既能提高抗剪承载力,也能有更大的挠度.
3.3 混凝土强度等级不同时的模拟结果
混凝土等级不同时荷载-跨中挠度关系见图17,试验和模拟值的极限荷载和挠度值见表7.
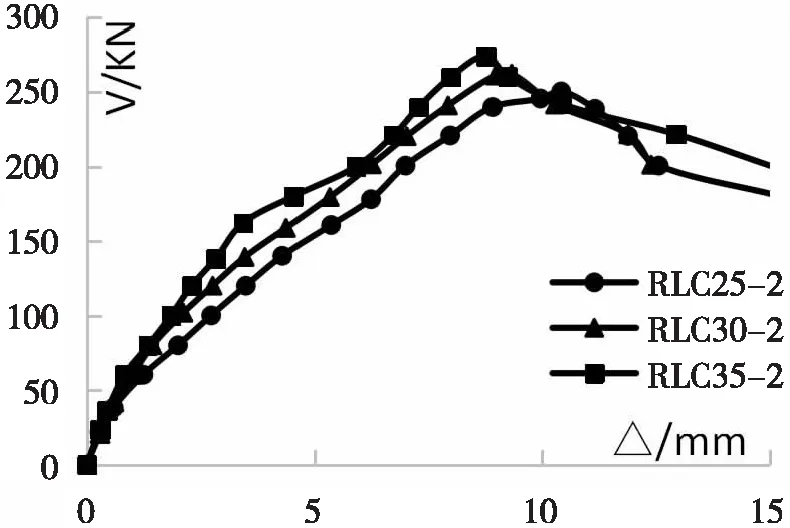
图17 混凝土等级不同荷载-跨中挠度关系

表7 混凝土等级不同时试验和模拟结果
从以上图表可知:随着轻骨料混凝土等级的提高,抗剪承载力得到了一定的提高,但跨中挠度变小了.
4 结 论
本文对于铁尾矿砂浮石混凝土的塑性损伤本构关系以及铁尾矿砂浮石混凝土梁模型进行了抗剪性能数值模拟,通过控制混凝土等级、剪跨比以及配箍率的不同,可以得到以下结论:
(1)对国内轻骨料混凝土塑性本构关系的研究和总结,并对各种本构关系进行模拟计算和比较,得到了最适合铁尾矿砂浮石混凝土的本构关系计算方法是《混凝土结构设计规范》GB 50010-2010里给出的本构关系,模拟出来的结果与试验结果相差不大.
(2)运用ABAQUS有限元软件对铁尾矿砂浮石混凝土梁进行抗剪性能模拟结果显示:剪跨比的减小可以使得混凝土梁的抗剪承载力得到提高,但变形能力最好的是在剪跨比为1.0~2.5之间.在设计铁尾矿砂浮石混凝土梁时,最合理的破坏形式是剪压破坏,不仅有很高的抗剪承载力,同时挠度也是最大的.
(3)配箍率和混凝土强度等级对铁尾矿砂浮石混凝土梁的影响没有剪跨比那么明显,混凝土强度越高,抗剪承载力就越大,但是挠度相对变小了.配箍率在一定的范围内,配箍率越大,抗剪承载力越大,跨中挠度越小.在铁尾矿砂浮石混凝土的应用中应合理的选取配箍率和混凝土强度.
