口算能力测查分析与教学启示
2020-09-02邬盼盼白丹娜王婵丹
邬盼盼 白丹娜 王婵丹


【摘 要】口算是运算的基础。测查学生的口算综合能力,可从测查方案制订、测查数据分析这两方面进行,并据此建立区域口算能力参照常模,针对口算算法相似度高、容易产生负迁移等现象,提出增加理法表征比较、立足单元整体教学、想笔算教口算的教学建议。
【关键词】口算;评价指标;教学建议
口算是运算的基础,口算能力会直接影响笔算、估算能力。教师对口算能力的认识及评价意识是否达到相应的水平?课题组对本区域25所学校的296名数学教师进行了调查,发现“三个不全面”现象:①口算测查内容不全面。96%的学校仅对“20以内加法”进行过关检测,对“表内乘除法”等其他口算内容均未涉及。②能力評价维度不全面。多数学校的能力测查主要以每分钟的正确题数作为评价依据,对算理、方法合理性均未涉及。③口算速度要求不全面。部分教师对课程标准中口算速度要求并不了解,存在要求过高或过低的现象。为此,制定切合本区域实际情况的口算能力评价标准迫在眉睫。
一、口算能力测查方案简介
人教版教材一至十二册中涉及的口算教学内容包括:20以内加减法口算、100以内加减法口算、表内乘除法口算、万以内数的加减法口算、多位数乘一位数口算、除数是一位数的除法口算及除数是两位数的除法口算。针对这些内容,测查可分三期进行:一是单元内容测查,可在单元内容学习之后或期末进行测查;二是阶段性口算能力测查,针对学生已学的口算内容;三是在四年级上学期学习完所有口算之后进行综合性口算检测,全面了解学生的口算能力水平。
每种测查都需设计测查方案,现以综合口算检测为例,方案如下。
(一)测查的维度
正确运算的维度,包括运算的正确性和运算的速度。算理理解和方法合理的维度,包括算理表述的正确性、算理迁移的通用性、运算方法的多样性。
(二)测查内容及水平划分
1.“正确运算”的要求标准
检测卷共有200题口算,图1是检测卷的第1列,每列都包含100以内的加减法口算、万以内数的加减口算、多位数乘一位数口算、除数是一位数以及除数是两位数的除法口算,每类各5题,每一列涉及的加减法、表内乘除法口诀均不同。根据学生答题的速度和正确率划分为水平0~水平3四个等级,具体标准如表1所示。
2.“算理理解”和“方法合理”的要求标准
检测要求:以图2为例,第一题测查学生对含有整十数口算算理的理解;第二题测查计算方法,让学生记录思考过程,分析学生的计算方法。
水平划分:根据学生答题情况,划分算理理解和方法合理水平。算理理解根据能否正确表述及迁移算理,分为四个水平;方法合理根据计算方法的多样性程度,分为四个水平。具体内容如表2所示。
二、区域综合性口算能力测查数据分析
(一)综合性口算四维数据统计及分析
根据表3~表6统计的数据表明,各层级学校在口算能力四维水平上存在差异。其中在速度和正确率维度上各层级学校差异较小,并且都保持了较高水平,这与平时学校、教师较重视口算速度与正确率有关。在算理理解和方法合理维度上各层级学校差异较大,且水平普遍偏低。在口算四维能力发展水平上,农村完小不均衡性特点显著。
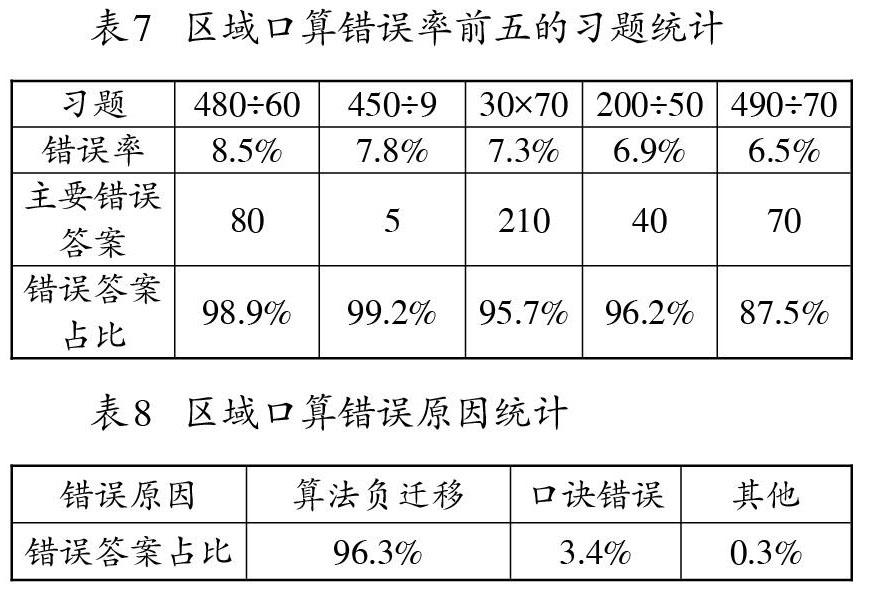
(二)习题错误率分析
根据表7~表8统计的数据表明,学生的错误主因是算法负迁移,如480÷60,错误答案“80”占比98.9%。这与口算算法相似度高有关系,这类口算教学中常用方法是转化为基本加减法或表内乘除法,运用“去零添零”“去零不添零”等方法进行口算,如“60+80,60×8,480÷6”在计算时都存在“先去零再添零”的过程,如计算“60+80”,先把60、80看作6个十、8个十,算出“6+8=14”,表示14个十,也就是140。但在计算480÷60时却只需要“去零”不需要“添零”,因此学生如果仅仅停留在算法的模仿上,很容易出现负迁移。
三、测查启示
(一)建立区域口算四维能力水平参照常模,明确发展目标
建立区域口算四维能力水平参照常模可避免出现要求过高或过低的现象,有利于改善全区学生的口算四维能力水平。结合区域测查结果,按城区、乡镇、农村三个层级,分别给出优秀、合格的参照常模数据如表9。
(二)加大理法表征的比较沟通,防止算法负迁移
针对学生容易混淆的含有整十数的口算算法,教师可以通过加大算理与算法表征的比较沟通,防止出现算法负迁移。
以除数是两位数的除法口算为例,作为口算最后一课时,需要全面梳理口算乘除法的算理算法,通过题组比较,系统构建口算方法。如在分析“80÷20为什么可以先算8÷2”时,应将表征多元化,通过小棒图、圈画图、计数器等进行说理分析,强化算理与算法的比较沟通。在巩固练习中加强变式训练,如“60÷2,60×20, 60÷20”围绕“积或商末尾为什么会出现0,出现几个0”进行算理和算法的分析,避免学生进入随意“添零去零”的误区。
(三)立足单元整体,想笔算学口算
在运算教学单元中,教材是按“口算(估算)→笔算”的顺序进行的。立足单元整体教学,可采用“倒叙”的思路(“笔算→口算”),通过笔算方法来逆推口算教学需承载的思想方法,从而确定口算教学的重点和难点,为笔算孕育必要的技能方法。以80÷20为例,学生在计算时主要有以下两种方法:①转化为表内除法,把80和20看作8个十和2个十,8÷2=4,80里面有4个20;②想乘算除,20×4=80,所以80÷20=4。本课之后将学习除数是两位数的笔算除法,学生最大的困难在于试商,如548÷81,需要把548和81先估成整十数试商,试商时需要用到( )×80接近550,这时想乘算除的口算方法就显得尤为重要,它是试商的基础。因此在教学除数是两位数的口算时,教师让学生用多样化的算法尝试计算后,要对“想乘算除”方法进行强化。同样,在计算除数是一位数的除法时,也需要有意识地强化“想乘算除”方法。
通过速度、正确率、算理理解及方法合理等口算能力评价,明确学生各维度水平层次,以及学习的难点、易错点,结合区域常模开展有针对性的强化练习,能真正提高学生的口算能力水平。