由静思动,发展学生的联系思维
2020-09-02费岭峰吴晓敏徐兆丹
费岭峰 吴晓敏 徐兆丹
【摘 要】联系思维是一种突出溯源、类比与贯通意识的思维方法,将其运用于数学学习中表现为发现数学知识的内在联系,寻找要素之间的关联点,打破点状思考问题的方式,形成立体的数学认知结构的思维过程。在人教版“认识几时几分”的内容学习中,将学生对“时刻”的认识由静止的状态上升到动態的状态,并开展“弱操作、强想象”的数学活动,以引导学生认识几时几分,从而有效发展学生的联系思维。
【关键词】小学数学;由静思动;联系思维;认识几时几分
所谓联系思维,体现在数学学习中,是指运用事物间存在着普遍联系的哲学观,努力发现数学知识的内在联系,寻找要素之间的关联点,从而打破点状思考问题的方式,形成立体的数学认知结构的思维过程。具体表现为三个特点:一是有溯源的意识,即从知识本质的维度思考问题;二是有类比的意识,即努力发现知识间的联结点;三是有贯通的意识,努力实现结构化的思考,促使知识成线、成网、成块。下面以人教版二年级上册“认识几时几分”一课为例,就如何在课堂教学中发展学生的联系思维谈谈我们的实践与思考。
【课前调查】学生对“几时几分”的认识究竟有怎样的基础水平?
“认识几时几分”是教材第七单元的内容。这一单元的知识是建立在一年级上册“认识钟面和整时”的基础上,主要包括认识几时几分及理解时分之间的关系,知道分针转动1格是1分,转动1圈是60分,知道“1时=60分”。为了解学生的学习基础,我们在课前选取一个班级共43名学生做了一次微调查。调查内容如下。
第一题:照样子,写出钟面上显示的时间(如图1)。
选用这道习题,主要在于调查学生对某个时间点(即时刻)的认读水平。调查结果如下:
调查结果表明,在认识类似“几时几分”这样的时刻时,分针刚过整时的时刻,学生认读难度较小,比如上题中的①和②;分针过半时的时刻,学生认读难度明显增加,如上题中的③。这与以往的经验相符,刚过整时的时刻认读中,分针靠近数字“12”比远离数字“12”更易出错。学生的典型错误有:将6时5分看成“6时1分”,将7时15分看成“7时3分”,将10时45分看成“11时9分”等等。
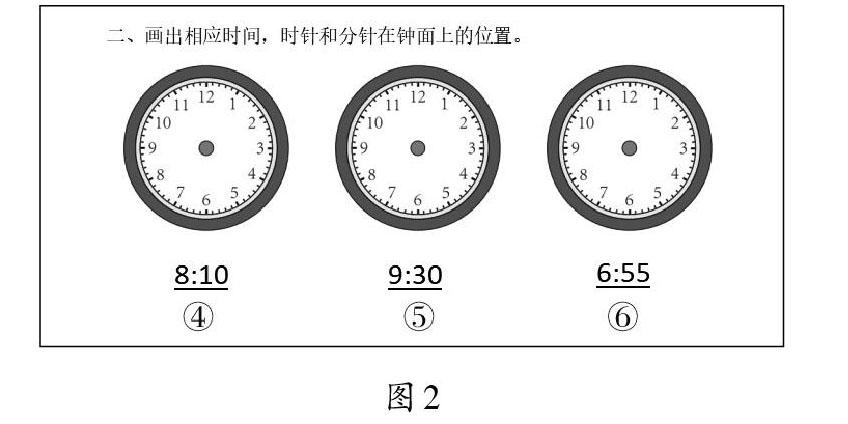
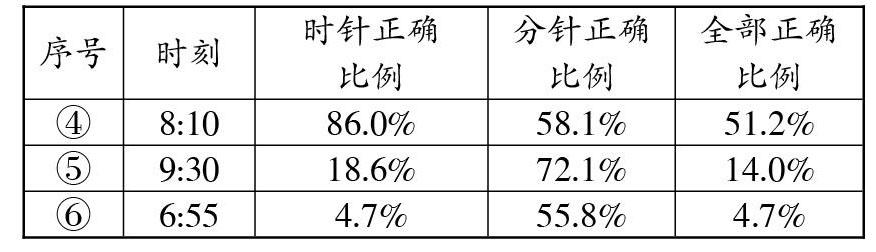
第二题:画出相应时间时针和分针在钟面上的位置(如图2)。
选用这道习题,意在通过画出相应时刻时针和分针在钟面上的位置,了解学生对具体时刻时针和分针的空间表达水平,同时也是了解学生对时针和分针联系思考的水平。调查结果如下:
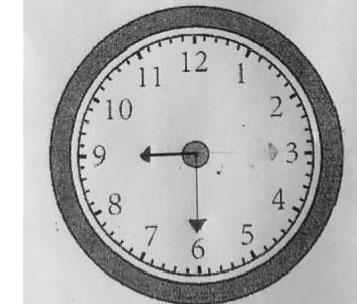
调查结果表明,刚过整时,难度较小;半时或将近整时,学生则比较容易忽略时针和分针的同步转动规律,出现错误。典型的有:画9时30分时,分针对着6,但时针仍然对着9(如图3);对于如“6时55分”这样的时刻,只有4.7%的学生能正确表示,说明对于此类时刻的认识是学生学习中的难点。
【文本解读】“认识几时几分”这节内容中需要思考哪些问题?
我们知道,时刻虽然只是个点,但在认识过程中,却需要理解它是怎样形成的,这也是本节课中寻求知识联系、发展联系思维的关键。因此,关于本节课内容的教学,我们需要思考以下三个问题。
一、“认识时间”仅仅是会认识某个时刻吗?
“认识时间”的教学,其实质是引导学生学会认识某个“时刻”,这也是本节课的基本目标。当然,在这个过程中,还包含着对钟面结构的进一步认知,即时针和分针的关系,分针转动1小格就是1分钟,转动1大格就是5分钟,转动1圈就是1小时;时针转动1大格就是1小时;分针在转动时,时针也同时在转动,只是两者转动的角度不同而已。这既是对“时间”作为一种量的知识的认识与理解,也是对时针、分针在钟面上所体现的“空间观”的具象支持。
二、如何引导学生对“时刻”的认识由静止认知上升到动态认知的水平?
对于某个“时刻”而言,那是一个固定的点,表现在钟面上,时针和分针有着固定的位置。然而,认识“时刻”的过程,无法仅通过静止的点来识读,而需要借助动态的过程,体会“几时几分”与“几时”之间的关系,由“几时”来识读相应的“几时几分”。唯有这样认识“几时几分”,才能帮助学生突破认读中的一些难点,如认识“几时55分”,时针与分针的同步转动,等等。也就是说,动态认识,既是学生认读时刻的学习方法,也是学生对时间认知能力的体现。
三、体验动态的过程中有没有比动手操作更有价值的学习方式?
我们在低段教学“认识钟表”与“认识时间”这些内容时,首先想到的引导方式是组织学生自己去操作,即在学具钟面上“拨某个时刻”。这种方式对于激发学生的学习兴趣,引导学生体验时刻的形成过程,有一定的积极意义。但在实际课堂上采用时,存在着两个方面的不足:一是低年级学生本就喜动,手里有个学具,会分散他们的学习注意力,使他们的思维游离于课堂学习之外,而且由于一般的学具操作起来不太方便,学生手部肌肉的灵活性本就存在差异,以致学生完成的速度快慢不一,不利于课堂的组织与调控;二是因为动手操作是一个具体的活动,钟面上有具象的时针和分针,且有些时针和分针本身就是联动的,学生只需拨动一根针,另一根针就自然随之转动,因而学生无须关注两根针的同步转动,不能暴露思维的问题,也就不利于学生思维的深度介入,不利于学生的深度思考。因此,我们认为,“画出钟面上时针和分针的位置”比直接动手操作更有利于学生自主思考、探索问题,并展示思维过程,也有利于教师发现学生的学习状况,从而给予更有针对性的指导。
基于以上思考,关于本节课内容的教学,我们制定了以下三个层面的学习目标。
1. 通过观察与交流,基本掌握几时几分的认读方法,理解几时几分与整时之间的关系,会认读几时几分。
2. 通过画、说、辩等方式,体会钟面上时针与分针的关系,认识时针和分针同步转动的现象,理解其本质。
3. 借助几时几分的学习过程,发展学生观察、比较、操作等能力,培养学生的时间观念。
以上三个目标中,目标1指向基本知识和基本能力的定位,目标2指向学习过程中学生思维的发展,目标3则指向数学基本活动经验的积累。综合分析整节课内容,“正确读写几时几分,理解几时几分与整时之间的关系”是重点,而难点则是对接近(不到)整时的认读(如几时55分)与时针、分针同步转动的理解。
【教学实践】如何引导学生准确理解“时针”与“分针”的动态联系?
整节课的教学,我们主要设计了“两画一认读”三个数学活动。
活动一:画9时5分,认识分针转动1小格就是1分钟。
复习旧知:8时。导入新课。
呈现9时5分,请学生先想象,然后尝试在钟面上画出这个时刻。
根据学生的作业进行交流(比较画了9时5分和画成9时25分的作业),认识分针转动1小格就是1分钟,转动5小格就是5分钟。
组织讨论画出了“9时5分”的作业。请学生说说想法。(板书:分针,1小格1分钟,1大格5分钟)
观看PPT,学生数时间,感受分针从12开始的转动过程以及单位时间的累积过程。
组织讨论画成“9时25分”的作业:你知道他画的是什么时间吗?你是怎么想的?
重点体现用不同的方法来得到分针的时间:一小格一小格数、用前一次的时间继续往下数、一大格一大格数、乘法口诀来算……
辨析“9时25分”时针的位置:你觉得时针的位置对吗?
观看PPT,得出感受:时针跟着分针走。
小结:看来要画几时几分,不仅要找准分针的位置,还要想着时针会跟着分针走。
(设计意图:通过画9时5分,了解学生的认知经验,发现学生的认知困难,从问题入手,引导学生理解认读某个时刻所需要的相关知识。其间,也真实地反映了学生的认识水平,为后续交流提供了依据,创造了必要的条件。)
活动二:画9时45分,认识分针与时针的同步转动。
呈现9时45分,请学生再次尝试画出这个时刻。
根据学生的作业组织反馈交流(比较时针的差异),强调时针和分针的同步性。说理(关注分针怎么数、时针的大概位置在哪里)。
利用9时55分过渡,感受时针接近10:时针看上去已经指着10了,你觉得它到了吗?那时针什么时候才正好对着10呢?(学生说想法后PPT演示)
引到10时,认识1时=60分。PPT完整展示9时到10时的过程。
教师结合学生的交流板书如下:
时针一大格 = 分针一圈
1小时 = 60分
小结:分针一圈时针一大格,周而复始,永不停止……
(设计意图:再画9时45分,一是检验前一个环节的学习效果,二是将难点分散在两个层次的活动中,即第一层次解决的是分针转动的问题,第二层次解决的则是时针的指向问题,然后通过两个环节中知识点的沟通,生成联系。)
活动三:结合情境认读时刻,突破与提升。
给出几个情境,请学生根据钟面上的时刻,认读时间。
根据学生的作业状况再次交流,关注难点,适度提升。
拓展练习,加深认识。隐去分针,只看时针估时间,用4:15,4:30和4:59三个时刻,组织游戏,交流讨论。
(设计意图:拓展性练习,再次回到想象,其意义基于本节课,又高于本节课。这样的活动,有一定的挑战性,是学生联系思维发展的重要活动经验。)
【教后再思考】
一、对钟面结构的认识是准确认识“几时几分”的基础
教学实践表明,将时间的认识置于钟面上进行,这其实已经达到了将“量”的计数与空间认识相结合的层面。因此,对钟面上12大格、60小格的结构的认识以及“分针转动1小格就是1分钟,转动5小格就是5分钟,时针转动1大格就是1小时”的经验,是学生认识“几时几分”的基础,也是学生理解“1时=60分”的基础。
二、时针与分针的动态联系是认识“几时几分”的核心
其实“认识几时几分”这节课的难点就是需要学生以“動态联系”的观点来理解“分针转动几小格,时针也会相应转动一定的角度”。比如,分针转动20小格,即转动了60小格(1圈)的三分之一,相应的时针也会转动某大格的三分之一。两者只是由于计量的单位不同(一个以“分”为计量单位,一个则以“时”为计量单位),造成转动角度的不同,其实际计量的时间长度则是一样的。由此,学生在理解“1时=60分”时,才能借助图示(转动1圈和转动1大格)建立起“时”与“分”的联系。
三、“弱操作、强想象”是培养学生联系思维的重要过程
操作是发现的过程,画出结果则是思考的过程。以钟面结构为基础,引导学生想象分针和时针的动态变化,不仅可以促使学生形成联系起来想问题的意识,同时也能强化学生对分针、时针联动的思维,积累相应的认知经验。可以客观地说,弱化操作,突出想象思考,是发展学生联系思维的重要目的,也是本节课教学的创新之处。当然,在实际教学中,弱化动手操作,并不是完全不去操作。当学生“画”出相应的时刻,并讨论交流了思考过程,有了相应的理解之后,以动手操作——“拨出相应时刻”进行验证确认,则能丰富学生的感性经验,强化学生的认识,让学生的理解更加深刻。这也是本课设计中需要加强的。