基于势函数聚类的改进RBF网络算法研究

黄朝辉， 闻辉， 车艳

( 莆田学院 信息工程学院， 福建 莆田 351100 )

0 引言

径向基函数(RBF)网络因其结构简单、稳定性强的优点，目前被广泛应用于工业诊断、图像分类以及语音识别等领域中.传统的优化RBF网络的算法包括k均值聚类(KMRBF)[1]、模糊C均值聚类(FCRBF)[2]和正交前向选择[3]，这些算法需要预先固定RBF网络隐节点的个数；但是固定隐节点的个数往往使得网络结构与实际问题不匹配，致使网络泛化性能下降.为了改善网络结构与实际问题不匹配的问题，一些基于序学习的RBF网络结构优化算法被相继提出.例如：文献[4]提出了一种最小资源分配网络(MRAN)模型，该模型通过统计邻近样本之间的相关性影响来删除部分冗余的隐节点，但该方法未能考虑样本空间的整体分布.文献[5]提出了一种基于序列增加和裁剪的RBF网络(GAP -RBF)模型，该模型通过度量RBF隐节点的重要性来规划学习策略，但该算法需设定样本服从统一分布.文献[6]在 GAP -RBF的基础上提出了一种泛化的 GAP -RBF (GGAP -RBF)模型，该模型虽然克服了 GAP -RBF 中样本需服从统一分布的问题，但是网络训练阶段的参数选取过于复杂.文献[7-8]提出了一种基于敏感度分析的RBF网络模型，该模型通过分析隐节点对整个网络的影响来动态调整RBF网络结构.上述文献研究的模型虽然可以建立自适应的RBF网络结构，但未能从整体上考虑不同样本之间的关联信息，因此网络的泛化性能会受到不同程度的影响.为此，本文提出一种基于势函数聚类的改进RBF网络算法，并通过双月人工数据集[9]以及UCI机器学习数据库[10]中的Blood Transfusion、Diabetes与Image Segmentation 3个基准数据集验证本文算法的有效性.

1 RBF网络算法原理

RBF网络由输入层、隐藏层和输出层3个模式层组成，其中输入层和隐藏层各节点的连接权值为1. 网络隐节点通常使用高斯核函数来实现对输入向量的映射.对于输入向量x∈Rh， 其经过隐节点的核映射后的输出可表示为

k=1,2,…,K.

(1)

其中μk(μk∈Rh)和σk分别为网络第k个隐节点的中心和核宽，K为RBF网络隐节点的个数.

RBF网络的输出可表示为

(2)

其中ωk为第k个隐节点与输出层对应节点之间的连接权值.

2 基于势函数聚类的改进RBF网络算法的实现

由于势函数可以度量样本空间中的两个不同向量随距离的变化情况，因此本文提出基于势函数聚类的改进RBF网络学习算法，即通过对样本空间的学习来增量生成不同的隐节点，以此实现对样本空间不同区域的有效覆盖.设x1和x2为样本空间的两个向量，γ(x1,x2)为由这两个样本建立的势函数.γ(x1,x2)的表达式为

(3)

其中：T为常数，用以控制势函数随距离变化的衰减速度；d(x1,x2)为x1,x2之间的距离.

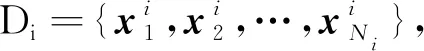
(4)

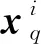
(5)

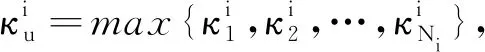
(6)

式中k为在RBF网络隐藏层中生成的高斯核个数.将高斯核宽σ与μk相结合，即可建立一个对应的高斯核用以实现对样本空间某个局部区域的有效覆盖.

q=1,2,…,Ni,q≠u.

(7)

3 实验及分析

为了验证本文所提算法的性能，将本文所提算法与4种典型的优化RBF网络算法(KMRBF、FCRBF、MRAN、GAP -RBF)进行实验对比.表1为不同分类数据集的信息.图3为双月人工数据集的结构图，图3中r=10,ω=6,d=-6.实验中各数据集中的样本全部归一化到[-1,1]范围内.将实验参数T和δ设置为T=1，δ=0.01,σ的取值为0.1～0.6.实验运行环境为Intel(R) Core (TM) i5-7500， 3.4 GHZ CPU， 8 G RAM， MATLAB 2013.

表1 不同分类数据集的信息

3.1 双月数据集下本文算法的学习效果

图4为训练集样本数为500且 核宽参数取不同值时的本文算法的学习效果.图4中每一个圆圈表示本文所建立的高斯核对样本空间的一次覆盖，且每一个圆圈都生成一个RBF网络隐节点.由图4可以看出，样本空间的覆盖区域随核宽参数的增加而增大，所生成的网络隐节点的个数及中心参数也随之改变，这表明本文所提算法具有良好的自适应性，可应用于复杂数据分类下的RBF网络隐节点个数以及参数估计.

3.2 双月数据集下不同算法的性能对比

图5为双月数据集下不同算法的性能.从图5(a)可以看出，随着训练样本个数的增加，本文算法生成的隐节点个数明显少于MRAN和GAP -RBF算法，但多于KMRBF算法.虽然本文算法生成的隐节点个数多于KMRBF算法，但因本文算法的隐节点个数是自动生成的，而KMRBF算法的隐节点个数需经过多次实验和手动设定才能实现，因此本文算法对样本空间具有更好地适应性.需要说明的是，在本实验中当FCRBF算法与KMRBF算法的隐节点个数相同时，FCRBF算法可以获取相对更高的分类精度，因此在图5(a)中未给出FCRBF算法.从图5(b)中可以看出，本文算法的分类精度优于KMRBF、FCRBF、GAP -RBF和MRAN算法，尤其是在训练样本个数为200～500时，本文算法的分类精度相对更高.

3.3 基准数据集下不同算法的性能对比

在UCI基准数据集下，本文算法与其他4种算法的性能对比见表2—表4.由表2—表4可以看出：本文算法的测试精度均优于其他4种算法.在隐节点个数方面，本文算法优于GAP -RBF算法和MRAN算法，但低于KMRBF算法和FCRBF算法.在Blood Transfusion基准数据集下，本文算法的训练时间优于GAP -RBF和MRAN算法，但略低于KMRBF和FCRBF算法；在Diabetes和Image Segmentation基准数据集下，本文算法的训练时间均优于其他4种算法.

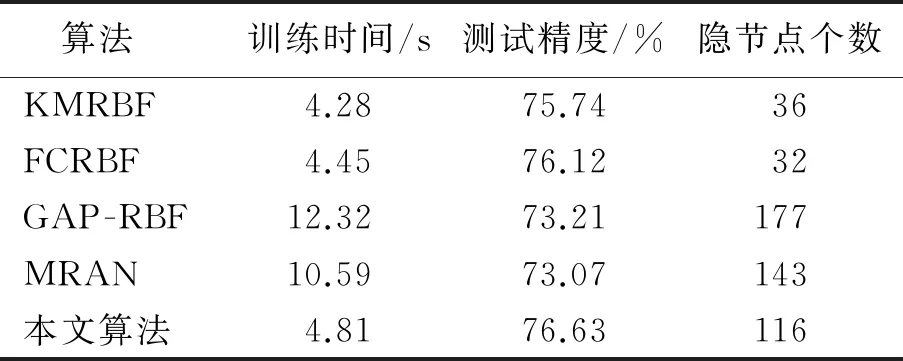
表2 Blood Transfusion基准数据集下不同算法的性能

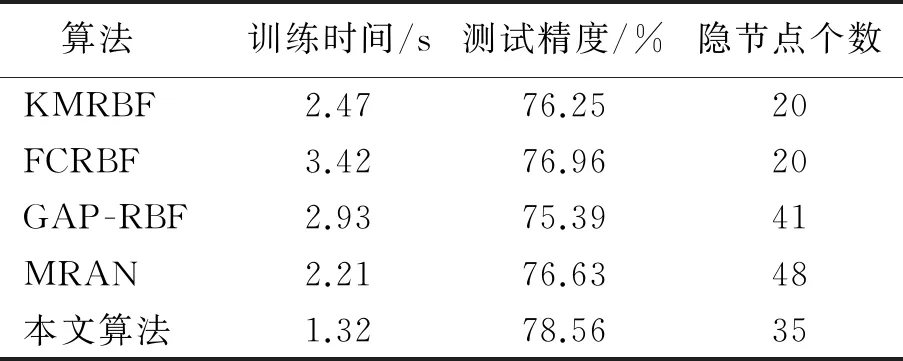
表3 Diabetes基准数据集下不同算法的性能

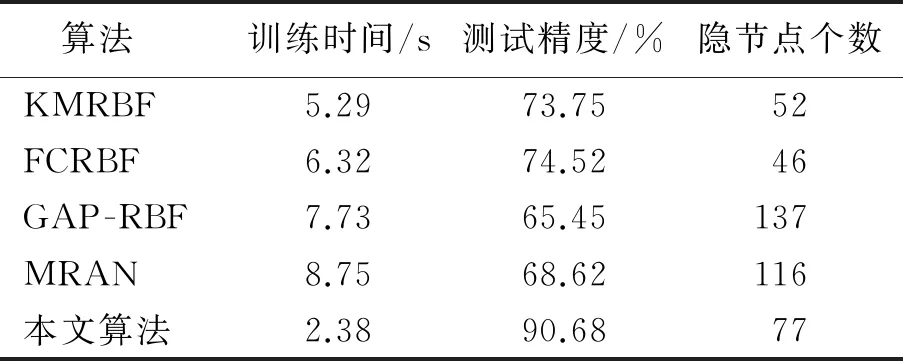
表4 Image Segmentation基准数据集下不同算法的性能

4 结论

研究表明，本文所提出的基于势函数聚类的改进RBF网络算法可有效利用样本空间的分布信息，并据此自动确定RBF隐节点的个数及参数.本文算法的分类精度优于KMRBF、FCRBF、GAP -RBF、MRAN 4种算法.与KMRBF和FCRBF算法相比，本文算法可以有效克服RRF网络结构需手动调整的问题；在Diabetes和Image Segmentation基准数据集上，本文算法的训练时间均优于上述4种算法；与 GAP -RBF 和MRAN算法相比，本文算法所得的网络结构更加简单，训练时间也相对更优.本文研究结果为优化RBF网络隐节点核参数提供了新的思路.本文在研究中未能考虑核宽的动态调整情况，因此在今后的研究中我们将引入核宽覆盖因子，建立样本空间的局部优化覆盖，以完善本文模型.