拟线性退化抛物方程组解的存在性和爆破性

林志强

( 福州理工学院， 福建 福州 350506 )

0 引言

文献[1-5]的作者研究了不同条件下的退化抛物型方程

受上述研究成果启发，本文将考虑拟线性退化抛物方程组

(1)

1 解的局部存在唯一性

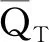
(2)

(3)

φ1(x,t)=φ2(x,t)=0,φ1(x,T)=φ2(x,T)=0.

证明构造如下问题(1)的近似问题:

(4)

由于问题(4)对于所有的确定εn 1和εn 2都是非退化的，因此根据Schauder不动点定理可得到问题(4)的解(un,vn).再由引理1得到问题(4)解的唯一性.以下分4个步骤证明序列(un,vn)的极限为(u(x,t),v(x,t))：

步骤1 考虑以下Cauchy问题：

U1(0)=|u0|L∞(Ω),V1(0)=|v0|L∞(Ω);

(5)

U2(0)=-|u0|L∞(Ω),V2(0)=-|v0|L∞(Ω).

(6)

易证存在一个依赖于|u0|L∞(Ω)和|v0|L∞(Ω)的常数t0(t0∈(0,T))， 使得式(5)和式(6)在[0,t0]上存在解(U1(t),V1(t))和(U2(t),V2(t)).再根据引理1有|un(x,t)|,|vn(x,t)|≤max{U1(t),V1(t),-U2(t),-V2(t)}.设T0=t0/2,C1=max{U1(t),V1(t),-U2(t),-V2(t)}， 则存在一个小的常数T0(T0>0)及一个正的常数C1(不依赖于n)， 使得

|un|L∞(QT0),|vn|L∞(QT0)≤C1.

(7)

步骤2 根据式(4)进行计算得：

(8)

步骤3 根据式(4)进行计算得：

有

其中常数C3>0, 并且对于小的η(η>0), 存在一个正的常数C3(不依赖于n)， 使得

(9)

因此通过自反序列理论和式(7)—(9)，可选择一个序列{un,vn}, 使得：

un→u,vn→v, (x,t)∈QT0;

(10)

(11)

(12)

unt→ut,vnt→vt, 弱收敛于L2(0,T0;L2(Ω));

(13)

(14)

(15)

(16)

(17)

根据式(7)、(10)和式(13)有：

其中φ1(x,t),φ2(x,t)∈C1,1(QT0),φ1(x,t),φ2(x,t)≥0.因式(16)和式(17)左边的结论与参考文献[10]中的定理2.1类似，故此处从略.

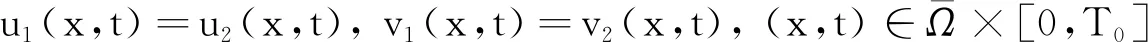
2 解的整体存在性

定理2假定(u0,v0)满足定理1， 且只要以下的一个条件成立，则方程组(1)的解整体存在:

1)p2q1<(m-1-p1)(n-1-q2).

2)p2q1=(m-1-p1)(n-1-q2)， 且|Ω|充分小或者a1,a2充分小.

3)p2q1>(m-1-p1)(n-1-q2)， 且初值u0(x),v0(x)充分小.

证明设φ1(x)和φ2(x)是下面椭圆问题的唯一解:

进而得

选取

则有

(18)

(19)

当a1和a2充分小时，选取a1和a2满足下列不等式：

由以上可知式(18)和式(19)成立.类似1)的证明，可得到解(u(x,t),v(x,t))整体存在.

3 解在有限时间内爆破

定理3假定(u0,v0)满足定理1， 且只要以下的一个条件成立，则方程组(1)的解在有限时刻爆破:

1)当m>2,n>2时，若p2q1>(m-1-p1)(n-1-q2), 且初值u0(x),v0(x)充分大.

2)当1

3)当m>2,n>2时，若p2q1=(m-1-p1)(n-1-q2), 且Ω包含一个充分大的球.

(20)

(21)

由于

其中Hx(w1),Hx(w2)是w1(x,t),w2(x,t)关于x的Hess矩阵，所以有：

当0≤yi≤A时， 1≤V(yi)≤1+A/2,V′(yi)≤0,i=1,2.对于充分小的T， 则有:

(22)

(23)

当yi≥A时，则V(yi)≤1,V′(yi)≤-1,i=1,2， 并且有：

(24)

(25)

当0≤y1≤A,y2≥A时，式(22)、(25)成立；当0≤y2≤A,y1≥A时， 式(23)、(24)成立.

1)当m>2,n>2,p2q1>(m-1-p1)(n-1-q2)时,有p2q1>(p1-1)(q2-1).选取充分小的σ1和σ2, 使

选取两个常数γ1,γ2>0, 使

由上式可得: (γ1+2σ1)(m-1)<γ1+1<γ1p1+γ2q1-2N(σ1+σ2)， (γ2+2σ2)(n-1)<γ2+1<γ1p2+γ2q2-2N(σ1+σ2).选取A>max{1,γ1/σ1,γ2/σ2}， 对于充分小的T>0则有:

由于φ1(0)>0,φ1(x)连续，因此存在两个常数ρ1>0,ρ2>0, 且对任意x∈B(0,ρi)⊂Ω,i=1,2， 都有φ1(x)≥ε.选择充分小的T(T>0)， 且满足B(0,RTσi)⊂B(0,ρi),i=1,2， 则在(x,t)∈∂Ω×(0,T)上有w1(x,t)≤0,w2(x,t)≤0.由式(20)和式(21)知，选取k0充分大时有(w1(x,0),w2(x,0))≤(k0φ1(x),k0φ1(x)).假定(u0(x),v0(x))≥(k0φ1(x),k0φ1(x))， 根据引理1可得(w1,w2)≤(u,v)， 并且(u,v)存在的时间不超过T.故解(u(x,t),v(x,t))在有限时刻爆破.

2)当1

选取两个常数γ1，γ2>0， 使

即(γ1+2σ1)(m-1)<γ1+1<γ1p1+γ2q1-2N(σ1+σ2)， (γ2+2σ2)(n-1)<γ2+1<γ1p2+γ2q2- 2N(σ1+σ2).选取A>max{1,γ1/σ1,γ2/σ2}， 对于充分小的T>0, 有：

由于φ1(0)>0,φ1(x)连续，因此存在两个常数ρ1>0,ρ2>0, 且对任意x∈B(0,ρi)⊂Ω,i=1,2， 都有φ1(x)≥ε.选择充分小的T(T>0)， 且满足B(0,RTσi)⊂B(0,ρi),i=1,2， 则在(x,t)∈∂Ω×(0,T)上有w1(x,t)≤0,w2(x,t)≤0.由式(20)和式(21)知，选取k0充分大时有(w1(x,0),w2(x,0))≤(k0φ1(x),k0φ1(x)).假定(u0(x),v0(x))≥(k0φ1(x),k0φ1(x))， 由引理1可得(w1,w2)≤(u,v)， 并且(u,v)存在的时间不超过T.故解(u(x,t),v(x,t))在有限时刻爆破.

3)当m>2,n>2,p2q1=(m-1-p1)(n-1-q2)时，选择两个常数l1>1,l2>1， 使

(m-1-p1)l1=q1l2>1, (n-1-q2)l2=p2l1>1.

不失一般性，假定0∈Ω.定义BR(0)是以0为圆心，R为半径的球，BR(0)⊂Ω.令φ1(r),φ2(r) (r=|x|)是下列椭圆问题的解:

考虑Cauchy问题：

s′(t)=min{(a1k1-1)/C1,(a2k2-1)/C2}sδ(t)，s(0)=s0.

w1(R,t)=sl1φ1(R)=0,w2(R,t)=sl2φ2(R)=0,t∈[0,T];

由引理1知在QT上(w1,w2)≤(u,v).由于(w1,w2)在有限时刻爆破，所以解(u(x,t),v(x,t))在有限时刻爆破.证毕.