一类矩阵迹方程正交解的一些研究

林志兴, 杨忠鹏, 陈梅香, 晏瑜敏

( 莆田学院 数学与金融学院， 福建 莆田 351100 )

0 引言

由于正交矩阵具有良好的运算性质，所以一直受到学者们的关注.文献[1]研究了用两个未知的正交矩阵求解线性系统的问题，文献[2-8]的作者分别研究了AX=B,XA=B和AXB=C等矩阵方程的对称正交解和反对称正交解问题，文献[9-10]给出了如下一个3阶的行列式为1的正交矩阵迹等式：

命题1设A为3阶正交矩阵(记A=(al j)∈O3×3)， 行列式|A|=1， 则

受命题1启发，本文从矩阵迹方程角度出发给出如下迹方程：

(1)

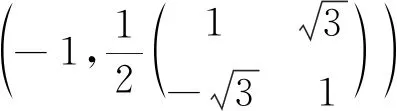
由例1可知命题1未包括迹方程(1)的全部正交解.以下本文将考虑更有意义的一般迹方程：

(2)

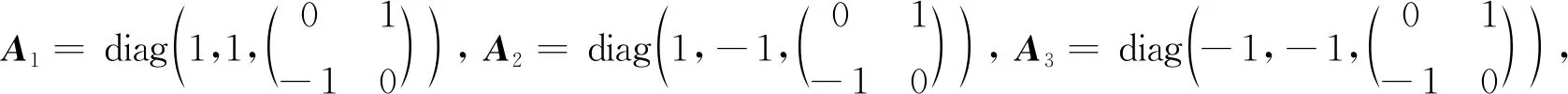
由例2可知A=(al j)∈O4×4是否为迹方程(2)的正交解与|A|=1没有关系.基于上述问题，本文应用正交矩阵的标准形和不变性，给出迹方程(2)有正交解的充分必要条件及其对称正交解的通解的显示表达，并指出不存在反对称正交解.为了讨论方便，下面给出各记号的说明.

设C为复数域,R为实数域，Z为所有整数的集合.E(En)为(n阶)单位矩阵，r(A)、AT、|A|、trA分别表示矩阵A的秩、转置、行列式、迹.复数i∈C满足i2=-1, 记|a|为a∈C的模.实矩阵A∈Rn ×n的特征多项式pA(x)=|xE-A|在C上的n个根(λ1,λ2,…,λn)为其特征值，且记σ(A)={λ1,λ2,…,λn}.如果ATA=E, 称A∈Rn ×n为正交矩阵.On ×n、SOn ×n和IOn ×n分别为n阶正交矩阵、对称正交矩阵和特征值全为实数或纯虚数正交矩阵的集合.当A∈Rn ×n满足AT=-A=A-1时，称其为反对称正交矩阵，类似于文献[2]用ASOn ×n表示n阶反对称正交矩阵的集合.以下总假设t,s分别为A=(al j)∈On ×n的特征值1和-1的重数，k为A两两共轭的非实特征值的对数.

1 正交矩阵为迹方程(2)的正交解的充要条件

引理1设A=(al j)∈On ×n,σ(A)={λ1,λ2,…,λn}， 则

|λj|=1,λj∈σ(A), 且 |A|=(-1)s, -1为A的s重特征值.

(3)

证明由文献[9]和[11]知|λj|=1， 进而由行列式性质可知式(3)成立.

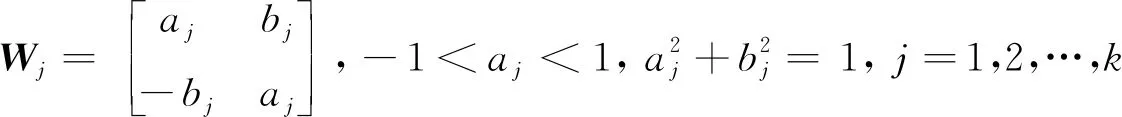
Q-1AQ=diag(Et,-Es,W1,…,Wk)=OA,t+s+2k=n,

(4)

且A∈SOn ×n⟺式(4)中k=0，A∈ASOn ×n⟺式(4)中t=s=0, 其中aj=0,bj=1,j=1,2,…,k.

证明由文献 [12-14]可得到正交标准形(4).由式(4)知A∈SOn ×n⟺式(4)中k=0,A∈ASOn ×n⟺式(4)中t=s=0, 其中aj=0,bj=1,j=1,2,…,k.

引理3[14]设A∈Rn×n,σ(A)={λ1,λ2,…,λn}， 则trA=-tr(-A),σ(-A)={-λ1,-λ2,…,-λn}， 且A∈On ×n⟺-A∈On ×n.

引理4设A∈Rn ×n, 如果pA(x)=|xE-A|=xn+c1xn -1+c2xn -2+…+cn -1x+cn, 则c1=

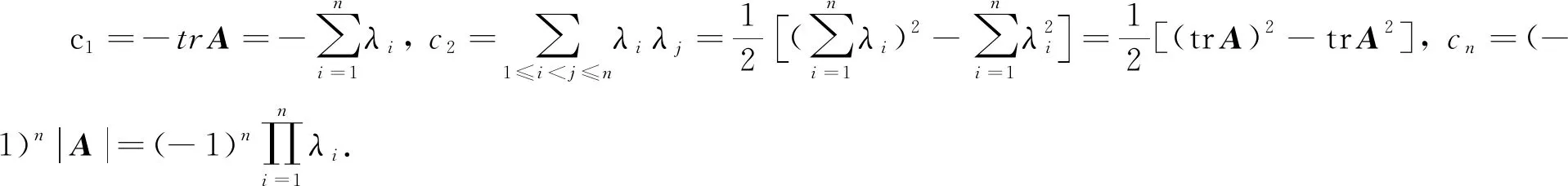
下面考虑迹方程(2)的“对偶”方程：

(5)

定理1设A=(al j)∈On ×n, 则：

(6)

(7)

A为矩阵迹方程(2)的正交解⟺ (trA)2-2trA=trA2,

(8)

A为矩阵迹方程(5)的正交解⟺ 2trA+(trA)2=trA2.

(9)

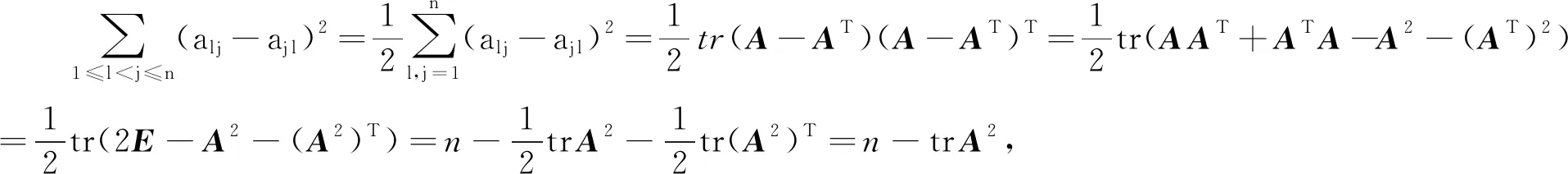
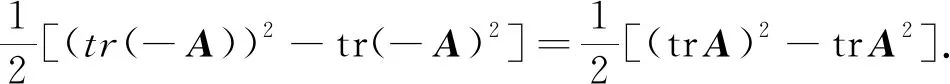
由式(6)即可得到式(8)，由式(5)和式(7)即可得到式(9).

式(6)和式(7)不仅给出了迹方程(2)和方程(5)有正交解A=(al j)∈On ×n的充要条件,而且还表明求解迹方程(2)和方程(5)的正交解就是确定矩阵迹方程(trA)2-2trA=trA2和(trA)2+2trA=trA2的正交解.因A和A2在迹相似下不变, 所以求迹方程(2)和方程(5)的正交解可转化为对正交矩阵的正交标准形的研究.由定理1和引理3可得以下推论:

推论1设A=(al j)∈On ×n, 则A是迹方程(2)或方程(5)的正交解⟺OA是迹方程(2)或方程(5)的正交解，且A满足迹方程(2)⟺B=-A满足迹方程(5).

推论1说明迹方程(2)和方程(5)的正交解是互为确定的,因此本文只讨论迹方程(2)的正交解.

2 迹方程(2)的所有特征值为实数或纯虚数的正交通解的显示表达式

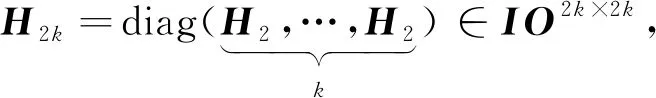
IOn ×n={A∈On ×n|OA=diag(Et,-Es,H2k)},t+s+2k=n.

(10)

引理5设A∈IOn ×n, 则:

trA=t-s∈Z, 0≤t,s≤n,A∈IOn ×n;

(11)

(12)

(13)

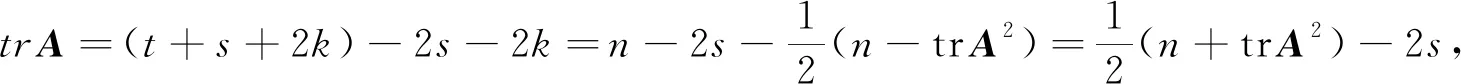
引理6设任意A∈IO2 ×2, 则A不满足迹方程(2).

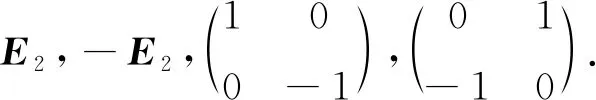
由引理6可知,讨论IOn ×n的迹方程(2)的正交解时设n≥3是合理的.以下用UIOn ×n表示迹方程(2)的IOn ×n正交解集合.

定理2设A=(al j)∈IOn ×n,n≥3， 则A∈UIOn ×n， 即A为迹方程(2)的正交解⟺

(14)

式中s,t都是非负的,同时

或

(15)

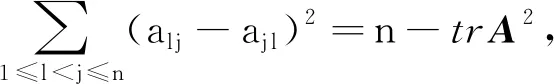
(trA-1)2=trA2+1, 当A∈UOn ×n时.

(16)

(17)

由式(17)知

(18)

或

(19)

当式(18)成立时,如果k=0， 则由n≥3和式(18)得

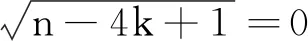
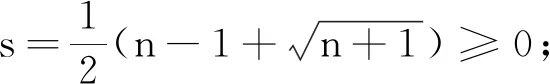
其次证明充分性.当式(14)成立且非负的t,s取式(15)的第1组数时, 由式(11)得

由例3可以看出，用式(10)中的正交标准形无法判定是否A∈IOn ×n， 因此本文给出以下实用的判别方法.

引理7设A∈On ×n， 则A∈IOn ×n⟺A2∈SOn ×n.

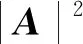
(20)

由bj≠0和式(20)中的2ajbj=0可知aj=0, 进而可知bj=±1.于是由引理2可知A的特征值为实数或纯虚数,即A∈IOn ×n.

由引理7知IOn ×n={A∈On ×n|A2∈SOn ×n}与式(10)等价，因此由定理2、引理8和推论1可得如下定理3成立.

定理3设A=(al j)∈On ×n,n≥3,A2∈SOn ×n,t和s由式(15)确定, 则

(21)

定理3给出了迹方程(2)的所有特征值为实数或纯虚数的正交解的简单实用的判定方法.设USOn ×n、UASOn ×n分别是迹方程(2)的对称正交解、反对称正交解的集合，则由引理2和引理7、式(10)、定理2和定理3、推论1可得如下定理4成立.

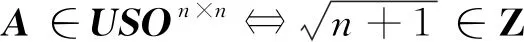
定理4不仅给出了迹方程(2)存在对称正交解的等价描述,还给出了迹方程(2)的对称正交解的通解表达.由引理2的结论和定理2可得定理5.

定理5不存在A∈ASOn ×n满足迹方程(2),即迹方程(2)的反对称正交解的集合UASOn ×n=∅.

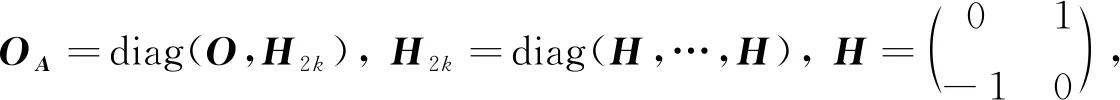
定理6设A=(al j)∈On ×n,n≥3, 且A2∈SOn ×n， 则A∈UOn ×n⟺ 4|n或4|n-3 (4整除n或4整除n-3).

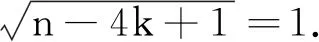
其次证明必要性.当n≥3时，如果对某个n有UIOn ×n≠∅且4|/n, 4|/n-3， 则必有4|n-1或4|n-2.当存在正整数q使得n=4q+1, 且A∈UIOn ×n时，由式(14)知有整数l∈Z使得n-4k+1=4(q-k)+2=l2， 因此存在t∈Z使得l=2t∈Z.于是可知有4(q-k)+2=4t2， 进而得到矛盾式1=2(t2-q+k).当存在正整数q使得n=4q+2, 且A∈UIOn ×n时，由式(14)知有整数l∈Z使得n-4k+1=4(q-k)+3=l2, 因此存在t∈Z使得l=2t+1∈Z.于是可知有4(q-k)+3=4t2+4t+1, 进而得到矛盾式 2=4(t2+t-q+k).必要性得证.

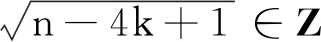
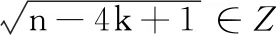
表1 满足的非负整数k及其对应的正交标准形

表1中数组(t,s,k)是正交标准形diag(Et,-Es,H2k)的简单记法.由定理3和定理4知，当n=5,6,9,10,13,14,17,18时,相应的UIOn ×n为空集，依此可列出3≤n≤20时矩阵迹方程(2)在相似意义下的UIOn ×n的全部元素.

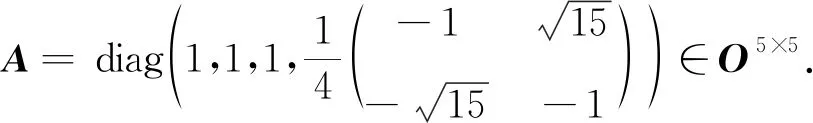
由例4知，当UIOn ×n=∅时,UOn ×n=∅不一定成立.