高中物理力学解题中整体法的应用方法分析

赵 彬

（江苏省江阴华士高级中学，江苏江阴 214421）

引 言

整体法指的是从整体角度审视、分析高中物理题的解题思想，尤其是在高中力学题中，教师可将物体运动的过程和结果、个体和整体、动态和静态相结合，详细了解物体运动环节的关联作用，从而剔除不必要的受力和运动分析，以梳理解题思路。

一、高中物理力学题中的整体思想

（一）整体法概念

整体法强调的是用整体的眼光去审题，将多个物体受力整合为一个整体受力，并分析多个力作用下物体的关系。教师将整体化思想应用到力学题中，能有效地解决学生在做题时视野过于局限的问题，能从全局角度对教学内容进行系统的总结和概括[1]。

（二）整体思想中的受力过程分析

在高中物理教学中，一般都涉及物体受力和运动以及多个物体之间互相作用。学生要判断有些力是否存在，在受力过程中物体的运动状态是怎样的。其一，学生要按照顺序来分析物体受力。一般题目中出现最多的是重力、摩擦力、弹力等。学生可以根据这些力产生的原因，分析时按“一重二弹三摩擦”的顺序。其二，确定受力的方向、数量等。力是矢量，有方向、有大小，如重力，方向竖直向下。弹力发生的条件是物体之间有接触，但是不同物体接触也不一定会产生弹力。所以面对不同的题目时，学生要结合条件来分析弹力的大小和方向。摩擦力中并不是两个物体接触就会产生摩擦力，学生要分析摩擦力产生的条件。

（三）整体法和隔离法的对比分析

表面上整体法和隔离法互相对立，但本质上二者存在一致性。整体法的思想是将多个物体当作一个整体进行分析，本质上也是将这个整体和它所处的环境隔离开，分析环境内其他物体对这个整体的力的作用。

整体法是从局部到全局的构思过程。运用整体法分析力学问题，可以让整体的受力情况更加明显，从整体的变化上来解释事物内部的变化，忽略不同环节的干涉和误导。相比较而言，隔离法是将一个整体拆分成若干组成部分，只分析其他部分对研究对象的力的作用，不考虑研究对象对其他事物的力。

尽管思维过程不同，但是在具体的解题过程中，整体法并不是和隔离法完全分割使用的，解题时两者可以互相融合、交叉，根据题目的特点灵活应用。

二、整体思想在不同力学概念中的应用

（一）系统内的物体存在相互作用时的整体思想

1.物体静止状态中的整体思想

例题1：已知在一个水平面上放置一个三角形，三角形斜面和水平面接触，在三角形一端α放置物体A，另一端β放置一物体B。已知三角形和A、B的质量分别为m0、mA、mB，且α＞β，mA＜mB，如果A、B都保持静止，求此时三角形斜面受到的摩擦力、支持力。

解析：根据题中条件，物体A、B都处在静止状态，那么可以用整体思想分析这道题，把斜面和A、B看作一个整体，它们之间的互相作用可以看作整体的内力，对问题的结果没有影响，所以忽略不计。

综合可得，这个整体受到的重力为：－（m0+mA+mB）g，又由于整体处在静止状态，那么这个物体受到的支持力也是－（m0+mA+mB）g，则在这个水平面上，整体不受到外力作用，摩擦力为零。

2.整体思想分析动力学知识

例题2：现在在一个光滑的斜面上部，用一根绳子将一根长木板拴住，已知倾斜角为θ。当松开绳子时，让一人甲往长木板上端跑，不考虑木板长度的影响，同时保持甲和斜面的相对角度不变。假设木板质量是甲质量的三倍，那么甲沿着木板奔跑时的加速度应该是多少？

解析：这道题考查的是用整体思想来解决动力问题。如果甲和斜面的位置保持不变，那么可以将甲和木板之间的相互作用看作内力不做分析。根据整体法思想，将甲和木板作为一个整体，由于整体只受重力作用，那么通过力的分解可知：绳子松开，整体向着斜面向下滑动，作用力为（M+m）gsinθ，结合题中条件：M板=3m甲，那么再结合牛顿第二定律，（M+m）gsinθ=ma，可得：a=4gsinθ。

（二）物体运动过程中整体思想的分析

1.整体思想体现在动能定理中

例题3，已知一斜面斜角α为60°，现将一物体以某速度从斜面低端O向上运动，滑动到S处A点时动能为E，继续向上滑动到B点时动能为零，并物体下滑。当下滑到OA中点D时，动能又为E，现知物体和斜面的摩擦µ=0.6，求问AB距离是多少？

解析：这道题是典型的运用整体思想来解读的力学动能题。一般学生在遇到这种题时，第一想法都是将不同阶段的运动单独分析。分析过程不仅复杂，还容易计算错误。运用整体思想，将该物体从A点到D点时的运动过程看作一个整体，不再分析整体内部各个点的运动状态。

分析过程如下：物体在运动过程中，重力和摩擦力同时发挥作用，物体的高度差、距离差会影响重力做功。物体在运动过程中同时受到摩擦力和重力的作用，并对其做功，影响重力做功的是物体运动的高度差或距离差，而对摩擦力作用产生影响是在运动全过程结合动能定理可知：求解可得：

2.机械能守恒定理中的整体思想

例题4，在光滑的水平面上有一根链条，已知长度为S，质量为M，让链条一半在水平面上，一半放在水平面外。将链条静止松开，则链条完全离开桌面时的速度是多少？

解析：在光滑水平面上没有任何阻碍的话，链条没有受到任何的外力作用。因此，这道题适用机械能守恒定律，题目给出条件是一半链条放在外面，而在思考和解题时要将链条看作一个整体，将光滑水平面看作零势能面，来分析链条整体的运动过程，即可得：

三、整体法在高中物理力学题中的实践解题分析

（一）整体角度构建解题思维

整体角度就是从整体观念，将系统看作一个整体进行分析，从而发现事物的变化特征。

例题5，在一个水平光滑桌面上放置两个物体A、B，如图1所示，已知mA=1kg，mB=2kg，一条无法伸长的细线连接物体A、B，F1水平向左，大小为10N，F2水平向右，大小为40N。两力同时作用，则求A和B之间的拉力。

解析：这道题运用整体法，不要把A、B 隔离开来分析，而是将它们作为一个整体，首先考虑由于细线不可伸长，确定A和B的加速度相同，先求出共同加速度：

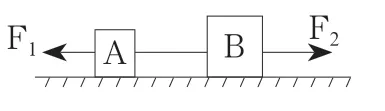
图1

继而分析个体，以A物体进行分析，由于受到拉力F和H1的共同作用，根据牛顿第二定律可得：F-F1=MAa，即F=F1+mAa=10+1×10=20N。

例题6，如图2所示，将一个质量为2kg的物体放在水平面上，动摩擦因数µ=0.2，在一个拉力为8N的水平拉力作用下，物体A沿着水平面运动了2s，然后将推力减小到6N，保持同样方向作用，物体又运动了2s，然后撤去外力。那么撤去外力之后物体还能滑行多长时间?

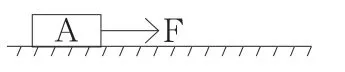
图2

解析：这道题用传统的做题法也能解决，就是按照题目中所给条件，来分析不同阶段的力的作用，运用隔离法分析。

第一阶段：F1t1-ft1=mv1，可得v1=4m/s。

第二阶段：F2t2-ft2=mv2-mv1，可得v2=6m/s。

第三阶段有-ft3=0-mv2，可得：t3=3s。

当然，如果用整体法，将全程运动看作一个整体，将全过程的动量表示为：F1t1+F2t2-f（t1+t2+t3）=ΔP=0，可得t3=3s。

通过比较可以看出，用隔离法分析的计算过程要比整体法复杂一些，计算也比较麻烦，而用整体思想考虑全过程的动量，不仅思路清晰，运算也更简洁，答题过程也比较简单。

（二）一动一静运动过程中的整体思想

对于一动一静的连接体，学生也可以用整体思想来解题。

例题7，如图3所示，将一个质量为M的木箱放在水平面上，在木箱的杆子上套着一个小球，质量为m。刚开始将小球放在杆子顶端，静止释放后，小球沿着杆子向下滑动，加速度是重力加速度的一半，即a=。那么在小球往下滑的过程中，木箱对地面的压力是多少？

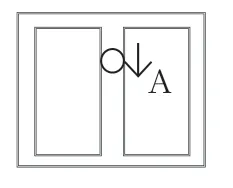
图3

解析：这道题可以结合整体思想，考虑到小球滑动时，木箱对地面的压力是处在一动一静状态中，依照牛顿第二定律：（mg+Mg）-FX=ma+Mx0，所以在这道题中，木箱所受的支持力为：根据牛顿第三定律，木箱对地面的压力为：

（三）将整体思想和隔离思想有效结合分析解题

对于整体思想来说，并不会完全隔绝分割思想，而是根据题目中的条件，适当地对其中有价值的条件进行隔离分析。所以将整体思维和分割法相融合，也是一种有效的解题手段。

结 语

物理是高中的一门重要课程，而力学是物理课程的重要组成部分，也是高考的重要考点之一。学生在学习时，不仅要分析物体受力，还要分析物体的运动特征，结合动静态分析，关注运动过程和结果等。整体法是立足培养学生从整体角度来分析物理力学问题的能力，让学生能在较短时间内找到合适的解题思路，以简化思维和计算过程，从而提高解题效率。因此，教师在开展力学时要加强对整体法的应用，不断提高学生的力学解题能力。