延长内曲线液压马达导轨疲劳寿命的研究
2020-08-17曾良才湛从昌
孙 龙,曾良才,方 明,湛从昌
(武汉科技大学机械自动化学院,湖北 武汉 430081)
1 引言
导轨作为内曲线径向柱塞式液压马达的关键零部件之一,内曲线液压马达出现故障大部分由于压力冲击造成导轨的失效引起的。国内外研究人员对内曲线液压马达压力冲击进行了许多研究,例如文献[1]对柱塞腔困油现象引起压力冲击进行了分析,文献[2]对液压马达背压不足引起压力冲击进行了仿真分析。但均未对由于马达转速变化出现的滚柱脱离导轨这个具体现象进行考虑,对其产生的压力冲击造成导轨的疲劳破坏未进行具体的分析。在马达转速变化的情况下,解出滚柱脱离导轨的具体位移变化情况,对其产生的冲击力与在该载荷下的导轨疲劳寿命的具体情况进行求解。为延长导轨的疲劳寿命,通过对导轨进行有限元优化分析,解出导轨结构参数与产生的冲击力、导轨疲劳寿命之间的变化关系,并选用最佳的导轨结构参数。为减小压力冲击,提高导轨的疲劳寿命提出一种优化结构的方法,提升了液压马达工作性能。
2 滚柱脱离导轨产生的冲击力
滚柱沿导轨不同区段运动时,导轨所受的各种力,现以回油区段加速区滚柱与导轨的作用力来分析其脱离导轨情况,如图1所示。当转速过大时,回油加速区背压力较小导致背压力与离心力之和小于加速度惯性力,使滚柱脱离导轨。根据该马达工作原理,滚柱不脱离导轨的条件是:

式中:Fg—滚柱作回转牵连运动时,因向心加速度而产生的离心力;Fp—始终压向导轨的液压力。

式中:m—滚柱的质量,kg;n—马达转速,r/min;aφ—滚柱的回油区加速度,由导轨曲线决定,mm3/s。
由式(1)确定滚柱不脱离导轨时转速与回油背压的关系:

式中:M1—回油背压,MPa;d—柱塞直径,mm;pgmin—滚柱到转子的最小中心距,由马达型号尺寸决定,mm。
由式(3)可以看出,当液压马达的尺寸参数确定后,施加在滚柱的回油背压与转速成反比,且回油背压过大会降低马达效率。由式(1)、式(2)可知当回油背压确定,马达的转速增大,导致滚柱在回油加速区时惯性力的增大,发生滚柱脱离导轨曲面的现象。滚柱在进入进油区后,在高压油作用下滚柱瞬时冲击导轨,产生巨大冲击力。

图1 滚柱与导轨间作用力Fig.1 Force of Roller and Guideway
3 内曲线液压马达动力学仿真
以某型号内曲线液压马达为研究对象,搭建了马达的主要运动部件,并添加材料、载荷和有关约束条件,对滚柱脱离导轨的现象进行动力学仿真分析[4]。
3.1 液压马达主要运动部件的材料、载荷和约束
(1)液压马达的主要零部件有内曲线定子导轨和运动部件转子、柱塞、滚柱,定子导轨采用50 号高强度钢,其他部件均采用结构钢。材料参数,如表1 所示。(2)根据马达工作原理,各部件之间的约束关系,如表2 所示。

表1 材料特性参数表Tab.1 Material Characteristic Parameters Table

表2 内曲线液压马达动力学模型中各部件之间的约束关系Tab.2 Constraints Among Components in Dynamic Model of Internal Curve Hydraulic Motor
3.2 液压马达仿真结果及分析
不同转速的滚柱位移曲线,如图2 所示。看从曲线1 可以看出,当马达转速为180r/min 时,随着进油口关闭,柱塞腔排油,滚柱位移逐渐减小,直至位移最低点165.25mm 处;当进油口开启,柱塞腔吸油,滚柱位移逐渐增大,滚柱紧紧压住马达导轨,可知曲线1 为滚柱未脱离导轨的位移曲线。随着马达转速增大,从曲线2 看出,当马达转速为270r/min 时,滚柱位移最低点降低到165mm,同时滚柱到达位移最低点时间明显的提前,这是由于马达转速增大,导致滚柱加速度惯性力过大,大于滚柱的背压力与离心力之和,使滚柱接近导轨最低点处脱离了导轨。通过对比曲线2 与曲线1 可知滚柱脱离导轨最长距离为0.4mm,然后在导轨最低点处瞬时进入进油区,柱塞腔瞬时通入高压油,使与柱塞连接的滚柱受到液压力瞬间与导轨发生了碰撞,从而引起对导轨曲面的冲击。

图2 不同转速对应的滚柱运动的位移曲线Fig.2 The Displacement Curve of the Roller Motion in Different Speeds
4 滚柱冲击导轨动力学模型
4.1 Newmark 理论算法
导轨失效是由于点蚀疲劳,故采用Newmark 算法,通过逐步施加边界载荷以增量方程的形式逐步求解,并在每一增量步内对静态平衡方程进行计算,更加精确[7]。
设X 为节点自由度,X˙为节点自由度相对时间变化率,X¨为节点加速度,M 为质量矩阵,K 为刚度矩阵,C 为阻尼矩阵,Ft为合力。
由达郎贝尔原理可得:

运用时间积分算法将位移和加速度在Δt 时间内进行有限差分展开:
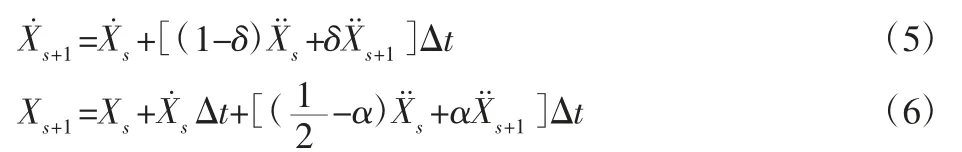
式中:α,δ—确保得到无条件稳定的积分参数,设定α=0.2525,δ=0.5050;时间间隔 Δt=ts+1-ts。
ts+1时刻的达朗贝尔方程:

将式(8)与式(9)代入式(10)经整理得:
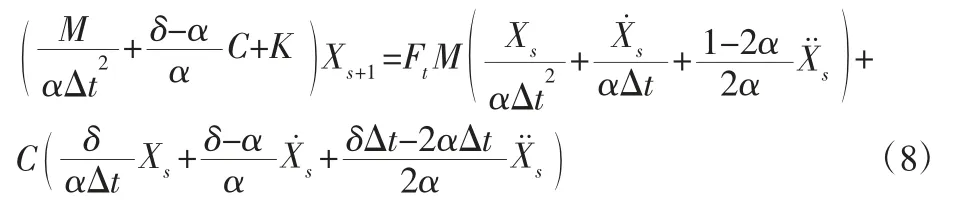
由式(8)求出 Xs+1,再由式(5)与式(6)计算出和。
4.2 滚柱冲击导轨有限元分析
由于导轨最低点的受力情况都是相同的,因此在马达实体模型的基础上,分出单个柱塞滚柱组件、内曲线导轨与转子模型。导轨的集中应力,如图3 所示。由此可知,导轨的最大应力为427.37MPa,已超过该材料疲劳极限341.5MPa[7]。这是由于马达转速由180r/min 变大到270r/min 时,滚柱的加速度惯性力增大,在向导轨最低点运动时脱离了导轨,滚柱脱离导轨0.4mm 后,在导轨最低点处瞬时进入进油区,在高压油的作用下,瞬间冲击导轨;且滚柱与导轨是线面接触,因此产生巨大的冲击力,是液压马达导轨出现失效的主要原理。

图3 脱缸时导轨应力云图Fig.3 The Stress Nephogram of Roller Deviates from the Guideway
4.3 马达导轨疲劳寿命的有限元分析
失效的一个种常见原因是疲劳,其破坏原因与频繁变载有关,而导轨最低点处承受脉动循环载荷。我们采用Goodman 方法对导轨最低点位置的平均应力进行处理[10],将实际的应力状态设为等效于平均应力,其值为零的受力状态,以得到等效于平均应力为零的S-N 曲线。Goodman 方法为:

式中:Δσ等—等效平均应力为零的应力幅;Δσ实—导轨实际应力幅;σ平—为导轨实际平均应力;σ强—强度极限。
在30MPa 工作压力下应用疲劳分析软件求解出当滚柱脱离导轨0.4mm 时,导轨的疲劳寿命。可知疲劳破环出现在导轨的最低点表面,导轨的位置随着远离导轨最低点其疲劳寿命逐渐增大,如图4 所示。而根据文献[8]可知出现疲劳破坏都在导轨的最低点表面,因此,导轨的最低点表面在该载荷下冲击201650 次后会出现疲劳失效[9]。

图4 脱缸时导轨疲劳寿命云图Fig.4 Fatigue Life Nephogram of Roller Deviates from the Guideway
5 提高导轨疲劳寿命的主要措施
在提高导轨疲劳寿命的主要措施中,可以对内曲线液压马达导轨的结构参数进行优化,能有效的提高导轨的使用寿命。
内曲线液压马达导轨的实际使用寿命往往要达(108~1010)次应力循环,所以用107的疲劳试验数据进行疲劳强度设计并不安全,且导轨材料50 号高强度钢的在1010次应力循环后仍会发生疲劳断裂[10]。因此,将以1010次应力循环作为标准来计算50 号高强度钢的疲劳强度。
马达导轨的原始结构尺寸:导轨宽度B=62 mm,导轨外径R=460 mm。经计算其作用间隔时间为0.04167s,折合工作时间64252.3 h,若液压马达每天工作12 h,则可以连续工作14.6 年。
将导轨尺寸设置为自变量,导轨的最大集中应力和疲劳寿命设置为因变量。液压马达自变量导轨宽度B 设置范围为(62~70)mm;自变量马达导轨外径R 设置范围为(450~470)mm。
由优化结果图5 得知,导轨外径从450mm 到462.5mm 最大集中应力逐渐减小,且462.5mm 到470mm 最大集中应力逐渐增大,而导轨最大集中应力宽度随着宽度增大而减小。导轨外径462.5mm 时最大集中应力最小,而考虑到滚柱的长度,选择导轨宽度选择70mm。所以在30MPa 的工作压力下,马达导轨外径462.5mm、宽度70mm 时最大集中应力最小,为286.35MPa。

图5 导轨外径和宽度对最大集中应力的影响Fig.5 The Influence of Guideway Diameter and Width on Maximum Stress Concentration of the Guideway
由图6 得知,同理,导轨外径在462.5mm 时,导轨发生疲劳破坏的循环次数最大,且导轨产生疲劳破坏的循环次数随着导轨宽度增大而增大,说明液压马达导轨在最佳尺寸为外径462.5mm、宽度70mm,其产生疲劳破坏的循环次数最大,为0.85082×1010。经计算折合工作时间98474.5.37h,若每天工作12h,可以连续工作22.5 年,导轨疲劳寿命得到提高。

图6 导轨外径和宽度对疲劳寿命的影响Fig.6 The Influence of Guideway Diameter and Width on the Fatigue Life
6 结论
(1)根据液压马达滚柱与导轨间作用力的分析,当转速增大,在进入回油区段加速区,滚柱的加速度惯性力增大,滚柱会脱离导轨,在进入进油区段加速区,滚柱冲击导轨产生冲击力。(2)对由滚柱脱离导轨这个因素产生的压力冲击与导轨的疲劳寿命的变化情况进行了的分析。根据内曲线液压马达工作原理建立动力学模型,定量的分析滚柱脱离导轨的距离变化,并具体求解出滚柱脱离导轨产生的冲击力与在该交变冲击载荷下的导轨疲劳寿命。(3)提出一种降低压力冲击,提高导轨使用寿命的有限元分析方法。本篇论文对导轨进行了响应曲面优化分析,解出液压马达导轨结构参数与产生的冲击力、导轨的使用寿命之间的关系,选择导轨尺寸参数,极大降低导轨受到的冲击力,提高导轨的使用寿命。
