3-SPS/1-S 张拉整体并联机构的研究与应用

郭京波 ，张海东 ，，纪志飞 ，李 杰

（1.石家庄铁道大学机械工程学院，河北 石家庄 050043；2.集美大学机械与能源工程学院，福建 厦门 361021）

1 引言

盾构管片是隧道的最终受力体，管片拼装质量是施工安全的重要影响因素[1]。管片拼装机是盾构施工实现衬砌安装的关键装备，其拼装质量、精度及效率直接影响隧道施工安全和进程。

并联机构是在动平台与基座之间包含2 个及以上串联运动链的闭环机构。学者们将其应用于盾构管片拼装机微调机构，具有承载能力强、精度高、刚度大等特点[2]，可获得更优性能。文献[3]构造3-SPS/S 并联机构，将其用于管片拼装机的姿态微调机构，实现3 个自由度的空间旋转；文献[4]对3-RPS 并联机构并进行运动学和动力学分析，并应用于管片拼装机设计方案；文献[5]基于3-PRPS 并联机构设计了管片拼装系统，可同时拼装两个管片，提高施工效率；文献[6]将3UPS-S 并联机构引入管片姿态微调机构，并进行了工作空间规划，空间内无奇异点；此外，文献[7]对用于管片拼装机的4-SPS-S 并联机构进行位置反解分析，推导出了雅克比矩阵，并给出了机构性能评价指标。张拉整体结构是一种在连续受拉的构件中包含离散受压构件，从形成的稳定自平衡结构[8]。张拉整体并联机构是近年来提出的新型并联机构，与传动刚性并联机构的区别主要是含有弹簧构件，具有更高的运动精度和灵活性。将3-SPS/1-S[9]张拉整体并联机构引入管片拼装机微调机构，分析位置反解、正解及工作空间问题，并进行数值验证。

2 方案设计与构型分析

管片拼装机微调机构要求实现3 个自由度的旋转，完成管片的横摇、俯仰及偏转动作，使前后两环及单环不同管片之间的螺栓孔准确对齐[6]，如图1 所示。要求机构具有很高的控制精度、承载能力及刚度。引入3-SPS/1-S 张拉整体并联机构为管片拼装机姿态微调机构，其拓扑结构，如图2 所示。该机构由上平台（运动平台）和下平台（固定基座）组成，上下平台均为等边三角形。下平台与管片拼装机主体相连，上平台为微调机构。机构有3 条SPS 结构的驱动支链，S 为球铰，P 为驱动副；K 为弹簧，3 个弹簧分别将基座与运动平台的铰点连接；此外，机构有一条S 结构的从动支链。3 条驱动支链、3 个弹簧及1 条从动支链将上下平台连接起来。

图1 管片拼装机结构图Fig.1 Segment Erector Structure Diagram

图2 3-SPS/1-S 张拉整体并联机构拓扑结构图Fig.2 Topology Structure of 3-SPS/1-S Tensegrity Parallel Mechanism

3-SPS/1-S 张拉整体并联机构自由度为：

式中：M—机构自由度数；d—机构阶数；n—构件总数；g—运动副总数；fi—第i 个运动副自由度数；v—冗余约束量；ζ—局部自由度数。

因此，机构自由度为3。由于驱动支链的存在，动平台没有沿X、Y、Z 轴的移动自由度，仅存在3 个转动自由度。引入该机构可实现管片拼装机的横摇、俯仰、偏转动作。

3 位置反解

在固定基座上建立一个定坐标系｛O｝-OXYZ ，在动平台上建立一个动坐标系｛O1｝-O1X1Y1Z1，O、O1分别为基座和运动平台的几何中心，如图2 所示。（1）运动平台位置变量：X=［x，y，z］T，式中：x、y、z—运动平台几何中心在｛O｝-OXYZ 下的坐标；（2）运动平台姿态变量：φ=［α，β，γ］T，式中：α、β、γ—运动平台绕 X、Y、Z轴的转角。令基座边长a，运动平台边长b。基座各铰点在｛O｝-OXYZ 下的位置为[9]：

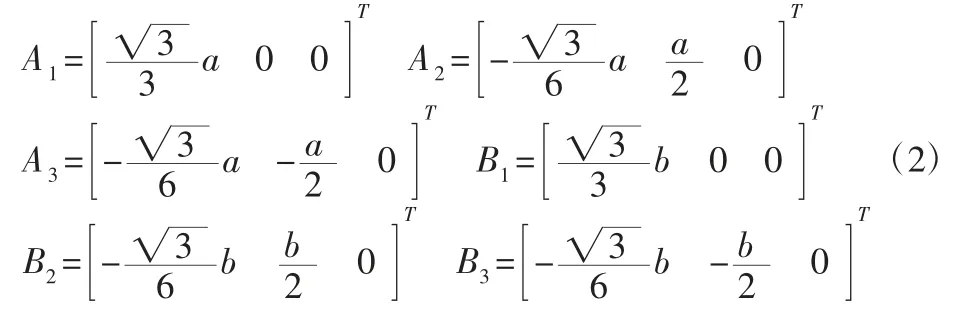
采用RPY 角[10]描述动坐标系的方位，则旋转矩阵为：

其中，sα=sinα，cβ=cosβ，其余类似。

由于运动平台仅具有α、β、γ 方向的3 个转动自由度，因此X、Y、Z 方向的位置变量可人为给定。则位置反解问题为给定X=［x，y，z］T情况下，依据输入变量 α、β、γ 求解驱动支链 Li的问题。

4 位置正解

基于变步长搜索法[9]的位置正解求解流程，如图3 所示。当已知驱动链长度，则输出变量在机构运动平台3 个转角α、β、γ 的变化范围内依据给定步长逐一搜索。若遍历整个范围后仍无法找到解值，则步长减半，重新搜索，如此往复。该方法无需给定初值，且不依赖于固定步长。

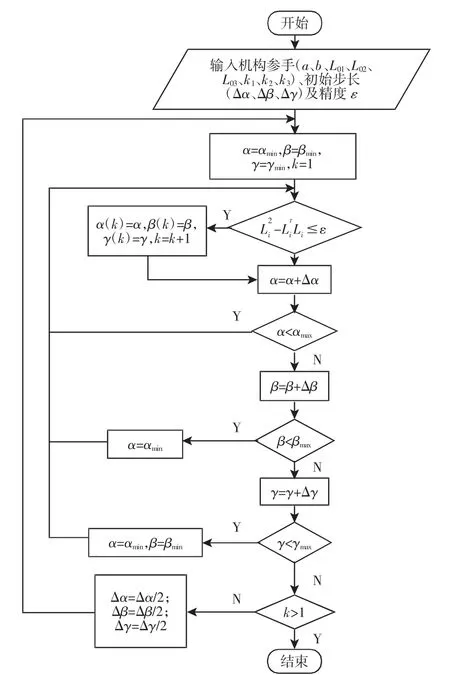
图3 位置正解变步长搜索法求解流程图Fig.3 Flow Chart of Inverse Position Solution Based on Variable-Step Search Solution Method

5 工作空间

运用数值方法求解机构工作空间。3-SPS/1-S 张拉整体并联机构具有 3 个输出变量 α、β、γ。Φ=［α，β，γ］T即为机构工作空间。工作空间约束方程为：

式中：r—驱动支链半径；Di—相邻两支链轴线段之间的最小距离；θmax—球铰的最大允许转角；θAi—固定平台球铰的转角；θBi—运动平台球铰的转角。

上述约束条件中，任何一个变量等于其边界值，所得解值便为工作空间的边界点。αmin、βmin、γmin是循环变量初值，αmax、βmax、γmax是循环变量终值。

假定工作空间由若干微元组成。每个微元对应机构上平台的一个可能位姿。当给出一个位姿时，判断其是否满足所有约束方程，若都满足，则说明该位姿存在，系统记录，然后给出下一个位姿，继续判断，如此循环往复。最后，系统搜索出所有存在的位姿，得到上平台工作空间范围。

由此，工作空间体积V[9]：

式中：length（X）—工作空间微元数量；Δα、Δβ、Δγ—3 个变量的搜索步长。

6 数值计算

6.1 位置反解数值算例

给定基本参数：上平台边长a=1m；下平台边长b=0.5m；弹簧原长Lk1=Lk2=Lk3=0.1m；弹簧弹性常数k1=k2=k3=0.5N/m。依据管片拼装机微调机构尺寸，令x=y=0，z=0.5m。

给定输入变量 X=［0，0，0.5］T，有：

同理可得L2和L3。

6.2 位置正解数值算例

给定驱动支链 L1、L2、L3，求 α、β、γ。精度 ε＝10-13，初始步长Δα＝Δβ＝Δγ＝0.15rad。计算得到 29 组解值，位置正解不唯一。前 10组位置正解，如表1 所示。

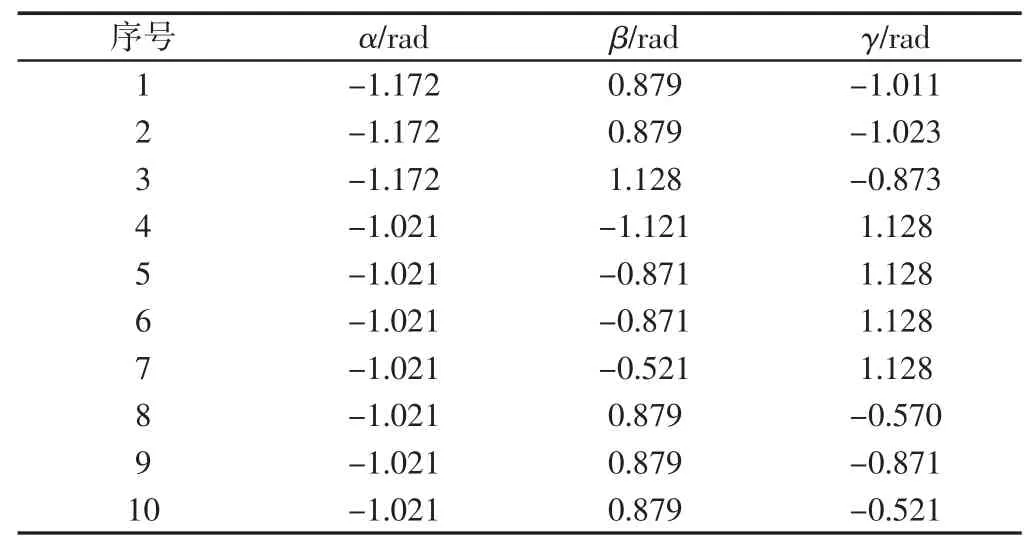
表1 前10 组位置正解Tab.1 Position Direct Solution of First 10 Sets

6.3 工作空间数值算例

运用Matlab 求解机构工作空间，如图4 所示。

图4 3-SPS/1-S 张拉整体并联机构工作空间Fig.4 Workspace of 3-SPS/1-S Tensegrity Parallel Mechanism

图中各点都是工作空间的微元，全部微元构成机构上平台的工作空间范围。运用式（7）可得：

改变θmax值，工作空间体积，如表2 所示。

表2 工作空间体积Tab.2 Workspace Volume

随着θmax变大，工作空间体积不断变大，θmax为45°时的工作空间体积是15°的196 倍。在管片拼装机的微调工作中，仅需完成3 个方向的小幅转动，因此较小的工作空间即可满足要求。

7 结论

（1）3-SPS/1-S 张拉整体并联机构具有3 个旋转自由度，将其引入管片拼装机，实现了横摇、俯仰及偏转3 个微调动作，且具有承载能力大的特点；与传统刚性并联机构相比，该机构存在3个弹簧，消除了运动副对机构产生的振动，提高了运动精度。

（2）针对3-SPS/1-S 张拉整体并联机构，推导了位置反解的求解方程，得到了驱动支链表达式；给出了位置正解的变步长搜索法求解流程。结合管片拼装机安装尺寸，进行数值算例验证，结果表明位置反解具有唯一性，但位置正解共有29 组解值。给出工作空间约束方程及体积求解方程，选定θmax为35°，得到工作空间可达范围是0.768rad3。