类桁架点阵多孔材料的研究进展

任晓雨，肖丽英，郝智秀

（清华大学机械工程系，设计工程研究所，北京 100084）

1 引言

多孔材料的优点在于其轻量化，多功能性和可设计性。根据多孔材料的微观结构可将多孔材料分为无序和有序两类[12]，前者主要包括开孔和闭孔的泡沫材料，后者主要包括蜂窝、类桁架点阵[11]以及一些其他由规则单元结构有序排列组成的材料。多孔材料的孔隙尺寸可以在毫米、微米直至纳米尺度变化。多孔材料有良好的能量吸收、传热和振动吸能特性[10]，在航空航天和汽车等领域有着很好的应用前景，例如利用其良好的传热性能，多孔金属材料可以用来制造散热装置，利用其轻量化的特点制造的零件可以减轻各类航天器的重量，利用其良好的吸能特性可以制造吸能部件等。多孔材料中的类桁架点阵材料可控变量很多，可设计性很强，所以类桁架点阵材料的类型、力学分析模型以及优化算法是多孔材料应用的关键，将不同类桁架点阵类型、力学分析模型和优化算法做了比较，并对之后的研究方向给出了自己的观点。

2 类桁架点阵材料单元结构的主要类型

不同类型的类桁架点阵材料主要是由于所选用的单元结构（unit cell）不同以及排布方向不同而产生的，组成多孔材料的不同单元结构可以归纳为以下几类。

2.1 Cross1，G6，G7 和 dobe-thin[13]单元结构

Cross1，G6，G7 以及 dobe-thin 是四种基本单元结构，从结构复杂程度上来讲，cross1 最简单，其次是G6 和G7，而dobe-thin最复杂，它们都可以看成是由长方形或者圆形截面的多根杆交汇组合而成，具体形状，如图1 所示。其中G7 单元结构在组成材料时绕内部锥体轴线旋转90°（G7r）后形成的材料整体会与G7 有很大不同。

图1 Cross1，G6，G7，dobe-thin 单元结构形状[13]Fig.1 The Structure of Cross1，G6，G7 and dobe-thin Unit Cell

文献[13]利用EBM 打印了利用上述五种单元结构组成的材料并测定了材料的力学参数如。他们的实验数据表明具有不同晶格类型的材料有着较大的性能差异，cross1 类型的孔隙率最大其次是G6、G7 和dobe thin 类型。总体来说孔隙率越大杨氏模量越小。同一种类单元类型在构成材料时排布方向不同也会对材料属性有较大影响，例如G7r 和G7 有着相同的孔隙率，但是G7r 的杨氏模量为G7 杨氏模量的一半。

2.2 八面体桁架（octet truss）单元结构

八面体桁架结构最早由文献[14]于1961 年申请专利，主要特点在于利用了空间最简单的几何体正四面体和八面体的组合填满整个空间，而不是利用单一的四面体填充空间，这样做的优势在于八面体和四面体的组合使得结构既简单又稳定而且可以完整填充整个空间。八面体桁架结构，如图2 所示。

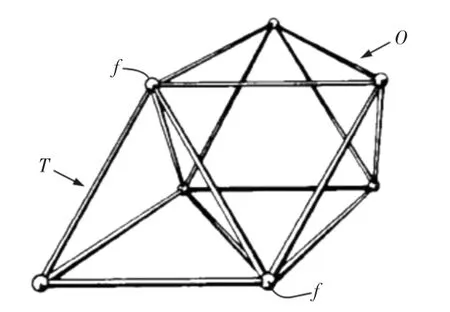
图2 八面体桁架结构Fig.2 The Structure of Octet Truss

2.3 仿骨单元结构（bone unit cell）

仿骨单元结构主要是模仿了骨内疏松的结构使得以仿骨单元结构组成的多孔材料更像真实的骨结构，这种材料一般用来作骨科植入物，这类结构的代表，如图3 所示。采用这种结构作为骨内植入物的结构单元主要是可以降低金属材料的杨氏模量使得植入物的杨氏模量更加接近人体骨的杨氏模量，保证成骨过程中对人骨的应力刺激，促进成骨过程。

图3 仿骨单元结构Fig.3 The Structure of Bone Unit Cell

以上这些单元结构除仿骨单元结构外都是由方形或者圆形截面的杆组成，cross1 型的单元结构最简单，八面体桁架结构比较稳定，但是这些单元结构都存在多根杆相交点，该点处会产生非线性变化的变形与力学特性，导致当采用简单梁单元假设分析这些单元结构或由此单元结构填充的零件时，分析结果会产生较大误差，因此需要针对类桁架单元结构建立更为精确的力学分析方法和模型。

3 类桁架点阵结构力学分析

当利用有限元方法对类桁架点阵多孔材料结构进行分析时，由于多孔材料结构本身尺度跨越范围大的原因，划分的网格数据量十分庞大，导致力学分析运算很慢甚至无法计算；如果利用有限元中梁单元分析方法，由于在类桁架点阵结构中多杆相交处会出现不满足梁单元假设的问题，导致分析结果精度不够甚至错误。基于以上问题研究工作者提出了一些具有针对性的力学分析方法，针对不同的类桁架点阵多孔材料单元结构提出了较为通用且有效的分析方法。

3.1 八面体桁架力学分析

文献[1]对八面体桁架（the octet-truss）类桁架点阵结构的力学分析方法进行了深入研究，分析中假设八面体类桁架点阵结构杆（strut）所交汇的节点处相当于铰接，而且杆只承受轴向载荷。八面体桁架结构由四面体和八面体两种基本单元构成，文献[1]认为八面体结构对于整体的力学性能影响更大，建立了基于八面体结构的力学分析方法，如式（1）、式（2）所示。

式中：ε—某应变；σ—应力；l—杆长；a—杆直径；Es—实心材料的杨氏模量；ρ¯—多孔材料的相对密度，对于八面体桁架结构其近似值可以通过公式得到。利用上述应力应变公式可以求得单个八面体桁架结构或者多个规律排列的八面体桁架结构的应力应变关系，其中关系矩阵［C］只有两个独立变量 s1和 s2，s3=（s1＋s2）/2。

图4 八面体桁架结构和坐标系Fig.4 The Structure and Coordinate System of Octet Truss

3.2 四面体夹心板力学分析

文献[4]研究了夹芯板的设计、计算和制造过程，夹芯板的基本结构是上下两层平面，中间以四面体类桁架点阵结构连接和支撑。他们首先讨论了以四面体类桁架点阵结构作为夹芯板内部支撑结构的失效形式，包括横向剪切失效、内部核心（四面体单元结构）的弯曲破坏失效、局部核心（四面体单元结构）的破坏失效以及像传统零件一样的弯曲失效、剪切卷曲失效和上下表面褶皱失效（表面与中间支撑层连接断开）[15]。然后分析了四面体类桁架点阵结构填充的夹芯板的数学模型。四面体单元结构的相对密度可以表示，如式（3）所示。ω 代表杆和底面投影的夹角，如图5 所示。t 代表杆的厚度，l 代表杆的长度。

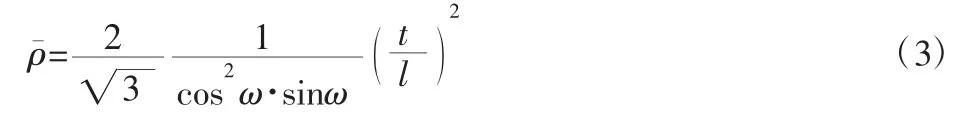
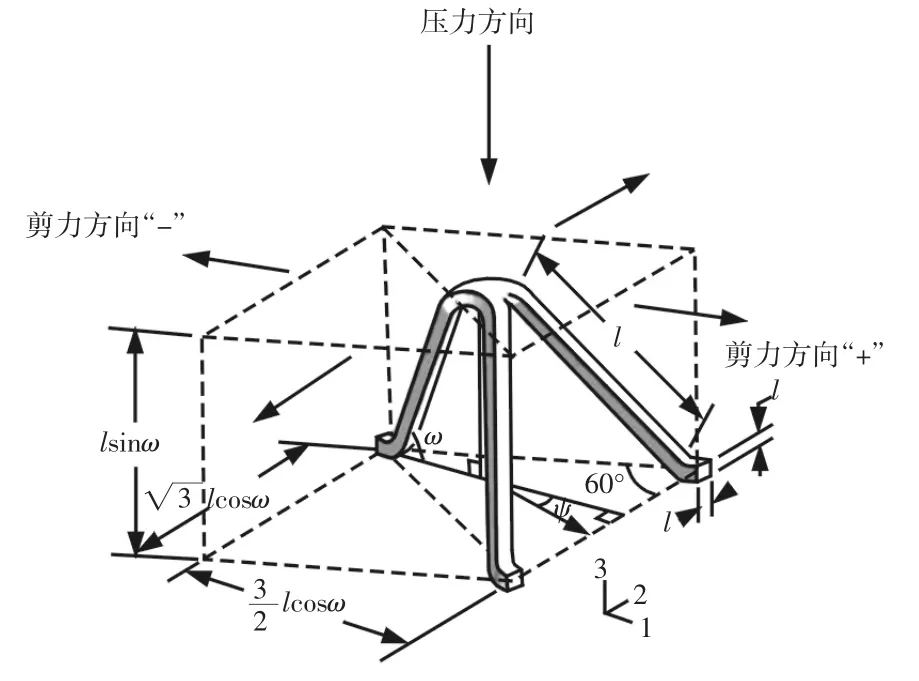
图5 夹心板内部的四面体支撑结构Fig.5 The Tetrahedral Unit Cell Used to Support the Sandwich Panel

四面体类桁架点阵结构外表面压缩刚度，如式（4）所示。其中E_s 是母合金的杨氏模量，ρ 为上述计算的相对密度，四面体类桁架点阵结构外表面剪切刚度，如式（5）所示。

夹芯板的四面体单元结构只填充了一层，但是多层的由其他桁架结构填充的零件或者形状在与外功能面相接时与夹芯板的方式相类似，所以他们在实际受力时也会遇到与夹芯板类似的失效形式或者失效情况，可以借鉴夹芯板的失效分析方法。

3.3 桁架单元结构有限元分析方法（unit truss approach FEA）

文献[2]对桁架类桁架点阵结构进行了研究并开发了一种力学分析方法—桁架单元结构有限元分析方法，传统的有限元分析方法首先将实体进行细密的网格划分，然后进行分析计算。桁架单元结构有限元方法是将类桁架点阵结构中的一种基本组成结构作为划分的基本单元，如图5 所示。将其作为类似于有限元分析中的网格一样对整个结构进行力学分析。这种方法可以实现对类桁架点阵结构的线性和非线性分析，文献[3]利用桁架单元结构有限元分析方法分别计算了单个，2×2，3×3 的八面体类桁架点阵结构的力学性能，也利用文献[1]的方法进行了计算，而且实际测试了实物的力学性能，最终得出的结论为桁架单元结构有限元分析方法与实际测量值的误差在10%左右，而文献[1]的方法误差很大，在n 大于等于2 的时候误差已经达到了60%。认为文献[1]的分析方法在n 大于等于2 时误差很大的原因在于这种方法是以八面体桁架单元作为整体的分析单元，相邻的八面体桁架单元有共用的节点，这种节点上有很多杆交汇处于非线性状态，而文献[1]的分析方法在分析多个单元结构的时候将相邻的单元结构完全以线性关系处理了，所以导致误差非常大。相对比而言，桁架单元结构有限元分析方法中计算模型的相邻单元之间是杆，而不是节点，在一定杆径比下杆可以看成是线性关系，所以在分析由多个单元构成的结构时按照线性关系计算仍然很准确。

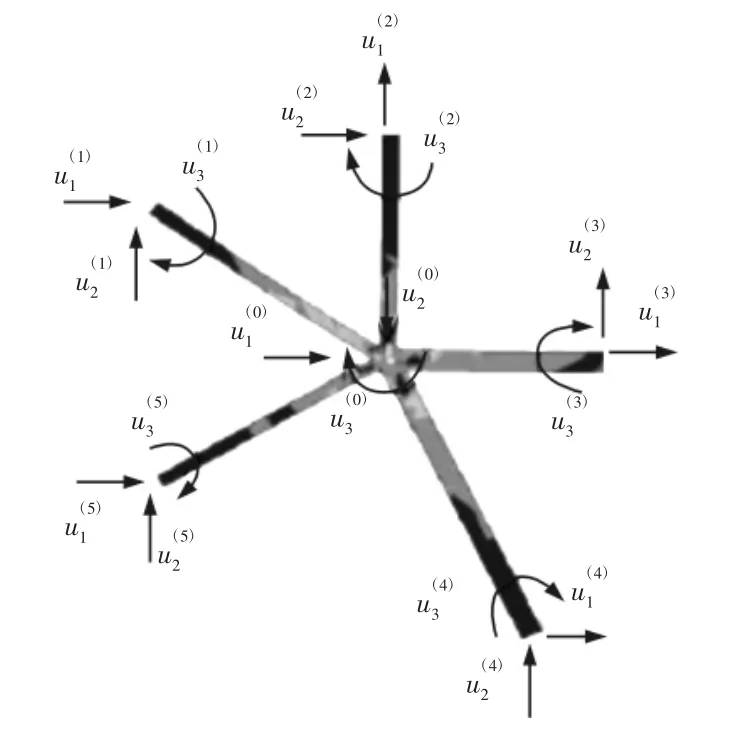
图6 桁架单元结构有限元分析方法的基本单元Fig.6 The Base Unit of Unit Truss Approach FEA

4 类桁架点阵结构优化方法

类桁架点阵结构的设计主要在于三个方面，尺寸优化、形状优化以及拓扑优化[5]，尺寸优化一般指类桁架点阵结构的杆径、单元长度和单元数量等参数的优化。在一定的边界条件下，对于类桁架多孔材料中的每一个单元结构都应该存在最优的杆径，这样尺寸优化就会产生和单元结构的数量相同量级的变量数目，如果单个单元结构中的不同杆的杆径也不相同，不同的单元结构有着不同的单元长度，那么变量数目会再增加一个数量级；形状优化指的是零件整体或者局部形状的优化，形状的优化往往难以作为独立的模块实现[6]，主要由于形状优化时一旦改变了形状，相应的有限元分析的模型或者网格划分也要发生变化，所以往往形状优化模块的开发需要将有限元分析融合在开发模块中；拓扑优化在类桁架点阵结构设计方面主要是指单元结构的空间排布位置和方向，拓扑结构对于整体结构的性能有着较大的影响。目前大部分的类桁架点阵结构优化算法侧重于尺寸优化，也就是在拓扑结构和形状基本确定的情况下优化单元结构杆直径和单元结构长度。这类优化算法可以归纳的优化框架[7]，如表1 所示。

表1 尺寸优化算法框架Tab.1 The Frame of Size Optimization Method

文献[7]对比了粒子群算法（PSO）和最小二乘法（LSM）两种算法。粒子群算法（PSO）的主要原理是模仿了鸟类的种群行为，在鸟类的种群行为中鸟类会根据个体经验和种群经验调整飞行运动，这种方式结合了局部搜索（个体经验）和全局搜索（种群经验）。这种算法首先在设计空间中随机创建很多粒子，之后根据式（6）更新速度，式（7）更新位置，其中速度公式中包含了个体飞行的惯性和个体飞行的经验以及种群飞行的经验。

最小二乘法（LSM）主要是利用了误差函数的梯度为零时，误差函数达到极小值，从而求得最优解。最小二乘问题的误差函数，如式（8）所示。

Pi，target表示第 i 个目标值，Pi，actual表示第 i 个目标量的实际值，X 是自变量组成的向量，从而只要求得X 向量使得S（X）函数取得极小值，X 即为满足目标值的最优解，也即S（X）的梯度为零时的 X 向量值。S（X）的梯度，如式（9）所示。

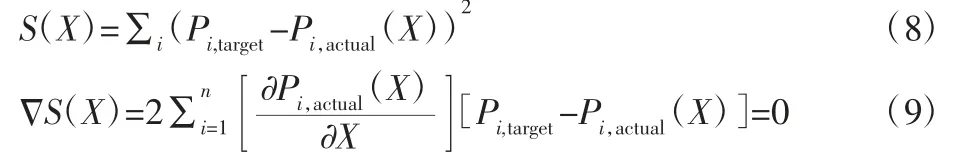
最终得到的结果表明LSM 方法比PSO 方法收敛快，而且在计算能力范围内LSM 每次计算都可以找到解，但是PSO 只有很小的概率可以找到解；在设计空间较大，参数进一步增多的时候PSO 有时会比LSM 收敛更快同时找到解。基于此一般采用LSM进行计算，只有当设计空间很大且不知道较好的初始解的时候再利用PSO 计算。

以上设计方法都存在计算开销大，设计时间长，对于大规模的设计空间难以很快给出优化结果的问题。为了减少类桁架点阵结构的设计时间，文献[8]开发了尺寸匹配和缩放方法，这种方法主要充分利用了有限元对于传统实体模型的分析结果和一个包含单元结构性能和尺寸的库，利用有限元对于传统实体模型的分析结果，结合单元结构性能和尺寸库为某一空间位置上的杆选取合适的尺寸。在这种方法之中，单元结构的空间排列方式已经确定，或者说零件所占空间区域已经被划分为与单元结构数目相等的小空间区域，同时根据零件有限元分析结果可以得到每个有限元节点上的应力结果，有限元的网格尺寸要远小于小空间区域的尺寸，所以每个小空间区域会包含很多有限元节点，将对应小空间区域内的所有有限元节点的应力值的平均值作为这个小空间区域填充的单元结构的应力评价标准，从而在前文提到的单元结构库中选取合适的单元结构杆径，利用优化框架[7]获得最大最小杆直径从而建立优化后的满足应力和变形的类桁架点阵结构模型。

目前的算法不能解决多载荷条件下的类桁架点阵结构设计，或者可以解决但是计算成本很大。针对这个问题文献[9]建立了一种新的算法：相对密度变换法（RDM），这种方法利用了拓扑优化过程中计算得到的有限元相对密度，采用一定的函数变换将相对密度和单元结构杆直径相对应，得到最终的类桁架点阵结构模型。RDM 的主要原理是类桁架点阵结构中杆的直径与对应位置拓扑优化结果中的相对密度成正相关。第j 根杆的截面积由公式（10）确定。

式中：Arj—第j 根杆的截面积；rij—第i 个拓扑优化有限元与第j根杆的距离；w（）—权重函数；ρi—第i 个拓扑优化有限元的相对密度大小。

权重函数选用了指数函数，使得距第j 根杆更近的有限元的相对密度在整个平均过程中占的权值更大。重新计算杆直径后将得到的模型进行一些处理，得到最终的类桁架点阵结构模型。这种算法利用了拓扑结构优化过程中得到的相对密度，所以不需要再次运行拓扑优化过程，减小了计算量，同时每根杆的直径既体现了局部特征也综合了整体密度特征。

5 总结和展望

近年来有关类桁架点阵结构的研究主要集中在如何建立更加精确的力学分析模型和如何减小搜索的设计空间方面。在力学分析模型方面，对于大规模的类桁架点阵结构设计目前采用比较多的方法主要是有限元分析中的梁分析和Hongqing Vincent Wang 的桁架结构力学分析方法，后者已经可以达到10%的误差精度。在减小搜索的设计空间方面，主要集中于利用有限元应力分析的结果或者拓扑优化的相对密度结果来减小设计空间，这两种方法都取得了比较好的设计结果，但是基于拓扑结构优化结果的算法可以解决多载荷问题。

未来有关类桁架点阵结构的研究建议主要在力学分析的精确性方面和拓扑优化两方面展开。在力学分析的精确性方面需要探索单元结构参数对刚度矩阵精度的影响。Hongqing Vincent Wang 的分析方法虽然可以达到10%的误差，但是单元的刚度矩阵是通过大量实例拟合的矩阵，这样得到的拟合矩阵难以进一步提高精度，而且不能获得影响精度的具体因素，所以为了提高力学分析的精确性需要进一步研究单元结构的哪些参数会影响到刚度矩阵的精确性，具体是如何影响的，然后得到一个含有这些影响因素作为变量的矩阵函数作为拟合函数，从而得到更加普适和精确的力学分析模型。进一步在结构设计和力学分析方面，还需要将加工工艺的影响因素考虑进去，根据不同的加工工艺得到相应的安全系数，从设计制造一体化角度提高产品的整体力学性能。此外，在拓扑优化方面提出采用综合有限元分析的应力结果和拓扑优化相对密度结果的方法来设计类桁架点阵结构单元的杆参数，进一步探索满足传热要求或者碰撞吸能要求的类桁架多孔材料设计方法。