一种含复合球副4-dof 并联机构运动学研究

张灿果 ，耿明超 ，路 懿

（1.河北建筑工程学院机械工程学院，河北 张家口 075024；2.燕山大学机械工程学院，河北 秦皇岛 066004）

1 引言

随着并联机构应用领域的不断拓展，少自由度并联机构在大型设备调姿、医疗器械、机械装备制造等领域得到了日益广泛的应用[1-2]。少自由度并联机构具有驱动分支少、没有多余自由度、控制相对容易等优点[3-4]。因此综合出工作空间大、比刚度高、运动性能好的少自由度并联机构对于研究并联机构运动特性、拓宽并联机构的应用领域具有重要战略意义[5]。复合球副同普通球副相比，具有结构紧凑、装配间隙小、运动范围大等特点，将复合球副应用于并联机构的型综合，可综合出性能良好的含复合球副少自由度并联机构。基于此设计出一种新型复合球副，利用该复合球副综合出一种含复合球副4-dof 并联机构。

并联机构运动学分析是进行动力学分析和刚度分析的基础。目前，并联机构运动学的解析方法主要采用螺旋理论法。Gallardo-Alvarado 等[6]应用螺旋理论对一种4-dof 并联机构的运动学和奇异性进行了解析，但是当并联机构的结构比较复杂时，应用该方法很难求解机构的加速度表达式。文献[7-8]采用矢量法分析了建立了几种少自由度并联机构运动学模型，但是当机构运动耦合程度较高时，该方法不再适用。以上方法各有特点，对于少自由度并联机构，由于机构自身的结构约束，部分并联驱动分支中存在约束力/矩，动平台运动时，动平台各个方向的运动相互耦合，其运动学模型的解析过程更加复杂。由于少自由度并联机构主动驱动小于6，一般情况下，采用上述一般方法建立的机构雅可比矩阵并非（6×6）的方阵[9]。这给机构的动力学解析和刚度分析带来了不便。基于部分驱动分支中存在的约束力/矩推导了含复合球副 4-dof 并联机构的（6×6）的 Jacobian 矩阵和 Hessian 矩阵，建立了动平台运动和各个驱动杆运动之间的映射关系。

2 含复合球副4-dof 并联机构

含复合球副4-dof 并联机构三维模型，如图1 所示。该并联机构由动平台、基座，连接基座和动平台的1 个复合球副分支和两个SPR 分支组成。复合球副分支由一个横梁、两个活塞杆、两个油缸和两个支座组成。两个活塞杆和上横梁两端使用转动副连接，两个油缸和两个支座同样使用转动副联接，支座固定在立环上，同基座固联。复合球副中两个驱动杆两端的四个转动副相互平行，形成一个平面机构，可以避免驱动杆承受弯矩，增大了机构的承载能力。复合球副分支中的横梁通过动柱和动平台联接，动柱与动平台、横梁分别使用轴线相互垂直的转动副联接。这样从复合球副中的活塞杆到动平台形成了一个复合球副（三个轴线相互垂直的转动副）。SPR 分支以球副和基座联结，以转动副和动平机台联结，转动副的轴线和动平台上平面平行。SPR 分支使用球副与基座联接，有效地增大了并联机构的工作空间。该机构具有以下特点：（1）机构中只含有移动副和转动副，制造方便，装配间隙小，运动范围大。（2）使用横梁将两个活塞杆连接起来，形成一个平面复合球副分支，可以避免驱动杆承受弯矩。

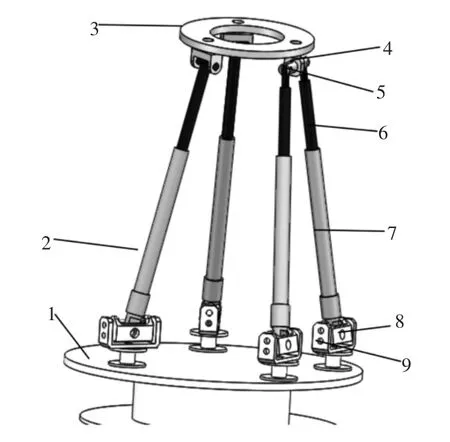
图1 含复合球副4-dof 并联机构三维模型Fig.1 3D Model of the 4-dof PM with Compound Spherical Joint

含复合球副4-dof 并联机构共有18 个构件，16 个转动副，4个移动副，每个复合球副分支含有2 个过约束，根据自由度计算公式得：

运用观察法[9]，SPR 分支中存在着过球副中心并且与SPR 分支中的P 副垂直、R 副轴线平行的约束力，当动平台在各个驱动分支的驱动下运动时，动平台在SPR 分支中约束力/矩的方向上必然没有运动，两个SPR 分支中的约束力方向和动平台的上平面平行。所以含复合球副4-dof 并联机构被约束的自由度为x，y方向的平移。该并联机构为三转一移的并联机构。

3 4-dof 并联机构运动学分析

并联机构运动学解析是进行动力学分析和刚度分析的基础，也是并联机构研究的基本问题。含复合球副4-dof 并联机构中，存在一个复合球副分支，两个SPR 分支，首先分析SPR 分支中驱动杆的速度。

3.1 SPR 分支运动分析

含复合球副4-dof 并联机构速度分析示意图，如图2 所示。等边三角形b1b2b3固定于动平台；其中心点为o。四边形B11B12B2B3固定于基座，B11B12的中点为B1，三角形B1B2B3为等边三角形，其中心点为O。连接基座端点Bi和动平台端点bi生成虚拟杆向量ri，设vri为虚拟杆速度大小，δi为虚拟杆的单位方向向量，v、ω 分别为动平台中心点o 的线速度和角速度，V 为动平台中心点的广义速度，ei为动平台中心点o 到端点bi的矢量。则：

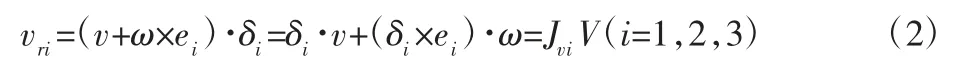
式中：Jvi—第i 个虚拟分支的雅克比矩阵；当i=1 时vri为复合球副分支中虚拟杆的线速度表达式，当i=2，3 时，vri为两个SPR分支线速度表达式。

图2 含复合球副4-dof 并联机构运动学分析框图Fig.2 Kinetostatics Model of the 4-dof PM with Compound Spherical Joint

设复合球副分支中支座的角速度大小和方向为ωiz和Riz，虚拟杆和支座之间角速度大小和方向为ωix和Rix，则复合球副分支中虚拟杆的角速度ωri表达式为：

式中：ri—第i 个虚拟杆的方向向量；Jωri—第i 个虚拟杆角速度雅可比矩阵。当i=1 时ωri为复合球副分支中虚拟杆的角速度表达式，当 i=2，3 时，ωri为两个 SPR 分支角速度表达式。

由于农村统计经费的短缺，导致很多农村统计人员只能在条件比较简陋的办公场所进行工作，有些统计人员根本就没有办公场所，所有的工作都只能在家中完成，同时也没有相关技术和设备的支持。有些农村基层统计人员只是靠简单的计算器进行工作，严重缺乏统计效率和质量。

式（2）对时间微分可得第i 个虚拟杆线加速度ari表达式为：

式中：A—动平台中心点广义加速度；Hvi—第i 个虚拟杆的Hessian矩阵。式（3）对时间微分可得虚拟杆角加速度表达式：

3.2 复合球副分支运动学分析

设vbij为复合球副分支中横梁端点bij的线速度矢量，δij为复合球副中驱动杆的单位向量，Jωbi为横梁中心bi的角速度雅可比矩阵，eij为横梁中心点bi至横梁端点bij的矢量。JVij为复合球副分支中驱动杆速度雅可比矩阵，则第i 个复合球副分支中第j 个驱动杆的线速度大小vrij的表达式为：

设第i 个复合球副分支中第j 个驱动杆的角速度为ωrij，上横梁和驱动杆之间的相对角速度的大小和矢量分别为：ωsj、Rsi，上横梁bi的角速度为ωbi，根据驱动杆和横梁之间的运动关系，则：

推导可得复合球副分支中驱动杆的角速度ωrij表达式为：

式（6）对时间微分可得到复合球副分支中驱动杆的线加速度arij表达式：

式（9）中，Hij即为复合球副分支驱动杆的Hessian 矩阵。式（8）对时间微分可得到复合球副分支中驱动杆的角加速度表达式：

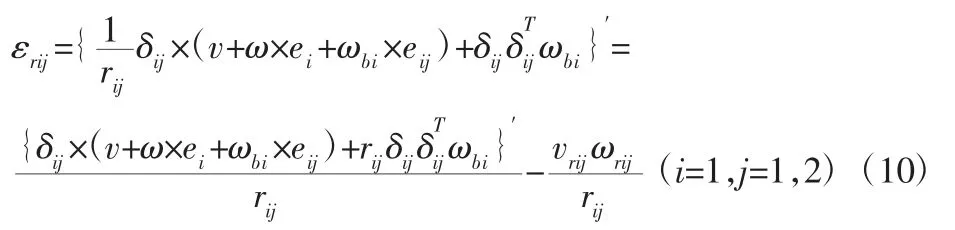
3.3 并联机构雅可比矩阵的建立

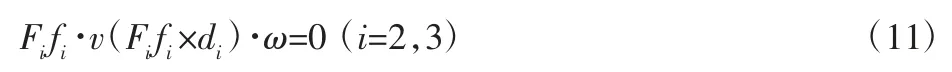
式中：Fi、fi—第 i 个 SPR 分支中约束力的大小和单位矢量；di—动平台原点o 到第i 个SPR 分支中约束力的矢距。

将式（2）、式（6）、式（11）合并，得到含复合球副 4--dof 并联机构标准雅可比矩阵。

其中，vr=［vr11vr12vr2vr30 0］T，J=［Jv11Jv12Jr2Jr2Jy2］T。

4 算例验证

4.1 算例验证

含复合球副4-dof 并联机构的运动学仿真验证采用虚拟样机技术。首先在Solidworksmotion 环境下建立含复合球副4-dof并联机构虚拟样机模型，该并联机构的结构参数，如表1 所示。设定机构中四个驱动杆相应的运动参数，如表1 所示。含复合球副4-dof 并联机构四个驱动杆的初始速度均为0mm/s2。虚拟仿真环境下测定含复合球副4-dof 并联机构四个驱动杆的角速度、角加速度作为此并联机构的运动学模拟仿真解，如图3、图4 所示。然后，测定并联机构运动仿真过程中动平台的位姿、速度和加速度作为已知参数。根据建立的含复合球副4-dof 并联机构的运动学模型，在Matlab 环境下编写程序，给定含复合球副4-dof 并联机构动平台的相关的运动参数，通过理论计算，求解并联机构四个驱动杆的角速度和角加速度，作为此并联机构的理论解析解，求解结果，如图5（b）、图5（d）所示。将理论解析解和模拟仿真解对比，即可完成含复合球副4-dof 并联机构的运动学验证。

表1 含复合球副4-dof 并联机构结构及运动参数Tab.1 Structural and Kinematic Parameters of the 4-dof PM

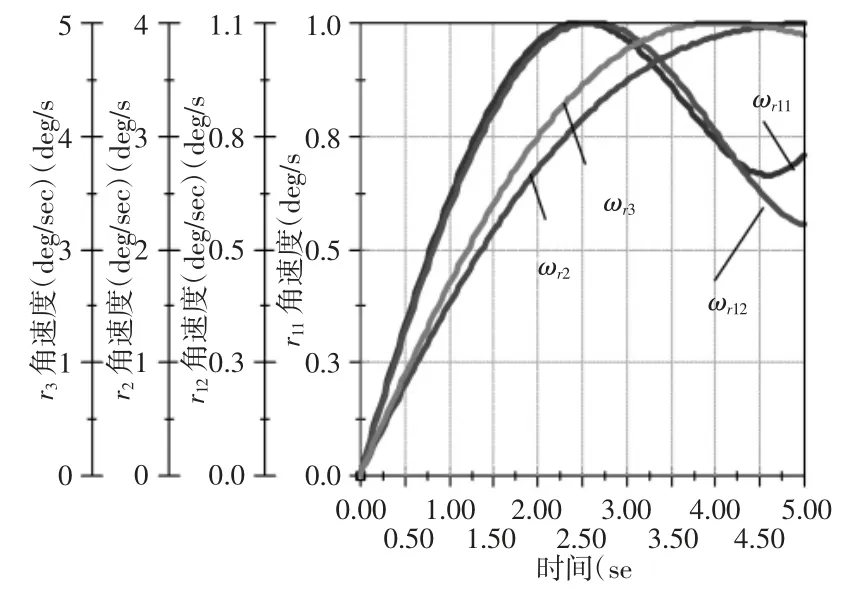
图3 含复合球副4-dof 并联机构驱动杆角速度模拟解Fig.3 Simulation Angular Velocity Solutions of the 4-dof PM

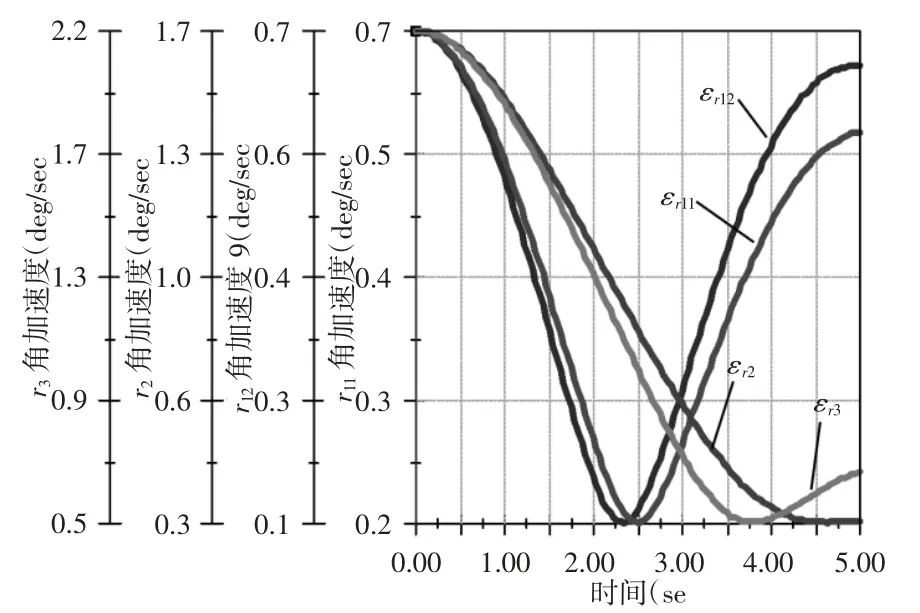
图4 含复合球副4--dof 并联机构驱动杆角加速度模拟解Fig.4 Simulation Angular Acceleration Solutions of the 4-dof PM

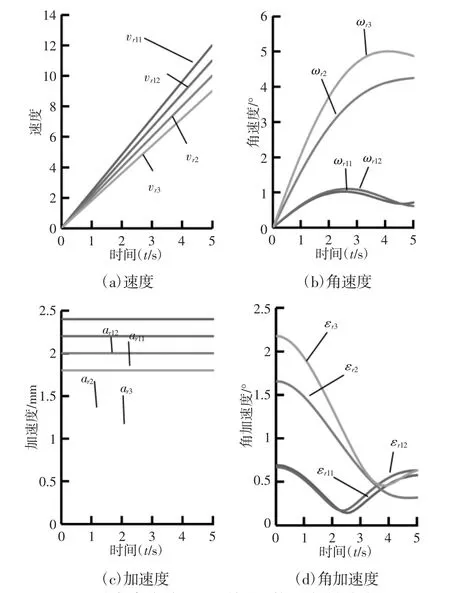
图5 含复合球副4--dof 并联机构运动学解析解Fig.5 Analytic Kinematics Solutions of the 4-dof PM

通过图3、图4 与图5 的对比，含复合球副4-dof 并联机构中驱动杆角速度、角加速度的理论解析解与模拟仿真解曲线高度一致。因此可以证明所建立的含复合球副4-dof 并联机构的运动学模型是正确的。

5 结论

（1）提出一种新型含复合球副4-dof 并联机构。该机构具有结构紧凑、制造容易、安装间隙小、工作空间大、承载能力强等特点。（2）建立了该并联机构的运动学模型。首先，根据矢量法分析了复合球副分支和SPR 分支的运动。基于虚功原理推导了关于约束力/矩的运动学方程。对速度雅可比矩阵方程式求导，求得该并联机构加速度的运动表达式，从而建立了动平台的运动和驱动分支件运动之间的映射关系。（3）在Solid works motion 环境下，对该并联机构进行动态仿真，仿真结果作为并联机构的运动学模拟仿真解。测定仿真过程中动平台中心点的位姿参数和运动参数。将上述数据作为输入数据，输入到该并联机构的运动学模型中，通过Mat lab 程序运算。得到该并联机构的理论解析解。用模拟仿真解和理论解析解对比验证运动学模型的正确性。