谈图形与几何中一线三等角的典例*
2020-08-13福建省龙岩莲东中学364000林晨晖
福建省龙岩莲东中学(364000) 林晨晖
在初中数学中,图形与几何是学习的重要内容,比如三角形全等就有着重要的地位.“一线三等角”的数学模型经常出现在近几年的考题中.所谓“一线三等角”是指在一条直线上出现了三个角相等.这种模型有类似的解题思路:只要有一条直线上出现了三个等角,往往也会存在一对全等(相似)三角形.因此,本文的重点是对这一模型进行探讨.加深学生对于题目条件的使用,提高问题解决的能力.在这个师生共同探讨的过程中鼓励学生尝试解题,并加强题后反思,培养他们解题的能力,让学生构建自己的知识体系,拓展知识面.下面我们来看“一线三等角”的一些典例.
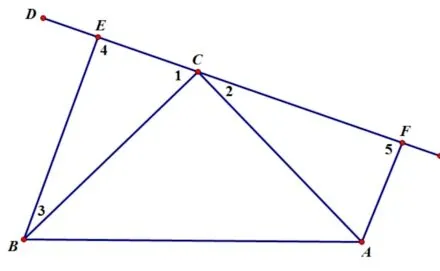
图1
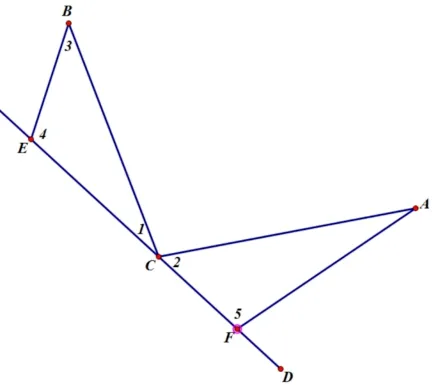
图2
例1如图1,AC=BC,∠5=∠4=∠ACB=90°,求证EF、BE、AF数量关系?
分析这是一线三等角的典例,直线MN上有三个直角,即∠4,∠5,∠ACB.DE、AD、BE是不在一条直线上的三个线段,因此要考虑线段的转化.根据图形看得出图中有一对全等三角形,再从此处下手,找出三角形全等的条件.
解:∵∠1+∠2=90°,∵∠1+∠3=90°,∴∠2=∠3(同角的余角相等),∠4=∠5,∠2=∠3,AC=BC.
∴ΔFAC≌ΔECB(AAS),∴AF=CE,CF=BE,∴EF=CE+CF=AF+BE(证毕).
上述例题难度属于中等.“一线三等角”模型变化万千,如果我们将这题改一下,改变模型中“三等角”的度数,那么这题的难度就加大了一些:
例2如图2,AC=BC,∠5=∠4=∠ACB.求证EF、BE、AF数量关系?
分析例1 中的“三等角”度数都是90°,例2 中也有三个角相等,但是度数不再限定.此题仍是在CD直线上有三个等角,分别是∠4,∠5,∠ACB.根据模型,这里必有一对全等三角形.因为三角形内角和为180°,所以∠4+∠1+∠3=180°,又因为∠FCE为平角,所以有:∠ACB+∠1+∠2=180°且∠4=∠ACB,所以得到了∠2=∠3,再由∠4=∠5、AC=AB,可以推断出ΔBCE≌ΔCAF(AAS).所以问题中三个线段的长度关系为:EF=CE+CF=AF+BE.同例1 的结论是一样的.
这样我们就将模型中“三等角”的度数从特殊推广到了一般.接下来,我们对直线的位置进行变化以下.上述两题都是直线CD在∠ACB的外部.现在,我们将直线CD画在∠ACB的内部,构造出“一线三等角”模型.
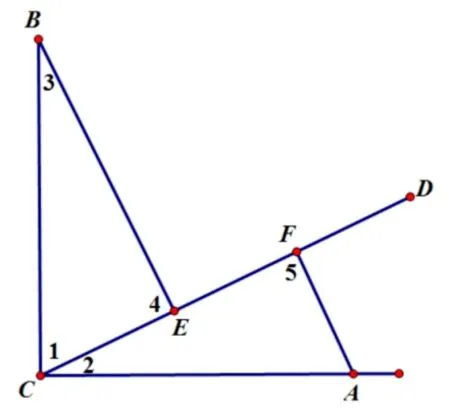
图3
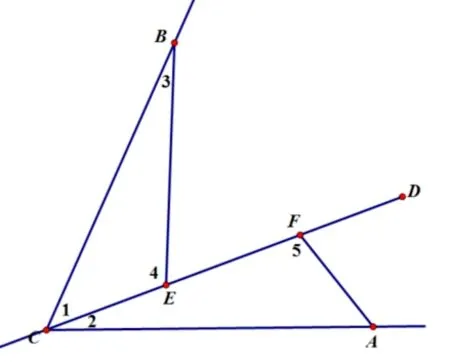
图4
例3如图3,CA=CB,且∠ACB=∠4=∠5=90°,求证EF、BE、AF数量关系?
分析刚才的直线CD在∠ACB外部,现在直线CD在∠ACB内部.在直线CD上有三个直角,分别是∠4、∠5、∠ACB.根据模型,其中必有一对全等三角形.根据同角的余角相等,所以可以得到∠2=∠3,再由∠4=∠5=90°、AC=AB,可以推出ΔBCE≌ΔCAF.所以问题中三个线段的长度关系为:EF=CF-CE=BE-AF.这样例3的结论就与例1、例2 的结论不一样了.
现在,我们保持直线CD在∠ACB内部不变,把“三等角”的度数由90°推广到一般度数,实现由特殊到一般的思想,看看结论是否发生变化.
例4如图4,CA=CB,∠4=∠5,∠4+∠ACB=180°,求EF、BE、AF数量关系?
分析在这例题里面,直线CD依然在∠ACB内部,但是相等的三个角不再是90°,它们的度数不被限定.此题中,直线CD上相等的三个等角分别是∠4 的补角、∠5 的补角、∠ACB.根据三角形内角和为180°,所以∠4+∠1+∠3=180°,又因为题目已知:∠4+∠1+∠2=180°,所以有∠2=∠3,再由∠4=∠5、AC=AB,可以推断出ΔBCE≌ΔCAF(AAS).所以问题中三个线段的长度关系为:EF=CF-CE=BE-AF.我们发现,改变了“三等角”的度数,但是只要直线CD在∠ACB内部,那么结论还是保持不变.
对“一线三等角”的基本模型探讨后,我们在看看它的其他形式:
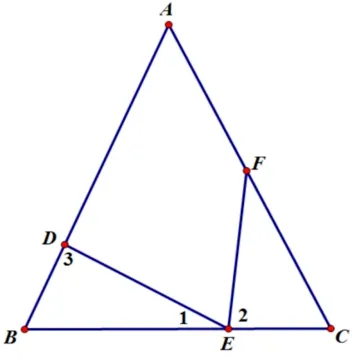
图5
例5如图5,∠B=∠C=∠DEF,DE=DF,请找出一对全等三角形,并证明.
分析在这题中,直线BC上三个 相等的 角是:∠B、∠C、∠DEF.此处必有全等三角形.根据三角形内角和为180°,所以∠1+∠B+∠3=180°,又因为∠BEC是平角,所以有∠1+∠DEF+∠2=180°,且因为∠B=∠DEF,所以有∠2=∠3.再由∠B=∠C、DE=DF,可以推断出ΔBED≌ΔCFE(AAS).在这题中,如果把DE=DF这个条件去掉,那么能得出的结论就是ΔBED∽ΔCFE.
因此,“一线三等角”的模型中隐含了三角形全等或者相似的条件.在考题中,有时候置换条件与结论,又是一种新题目.因此,我们在教学中要挖掘出这种类型题目可能会考的模式,参透此类型题,构造出解题的模式.
