一个三角函数配角公式及其应用

江苏省盱眙中学(211700) 董培仁

苏教版高中数学必修4 第107 页有这样的例题:

例求函数的最大值.

处理此题最重要的一步是将函数化为一个角的一个三角函数的形式,即:y=sinxcos+cosxsin=sin(x+),然后再求得最大值1.

一般地,将asinx+bcosx(a,b不全为0)化为rsin(x+φ)或rcos(x-φ)的形式,在三角运算中经常涉及,但教材中并没有把asinx+bcosx=rsin(x+φ)(或rcos(x-φ))作为公式,通常只是作为一种方法呈现.教学中我们发现,作为公式进行推导并揭示公式的意义,可以促进学生深刻理解并迅速准确地应用.

1 三角函数配角公式的推导及其配角意义的探讨

1.1 正弦型配角公式

基于两角和的正弦公式sin(α+β)=sinαcosβ+cosαsinβ,可作以下考虑:

设asinx+bcosx=rsin(x+φ),将式展开,则asinx+bcosx=r(sinxcosφ+cosxsinφ),所以a=rcosφ,b=rsinφ(其中r＞0),则a2+b2=(rcosφ)2+(rsinφ)2=r2(cos2φ+sin2φ)=r2,所以r=于是得到

因此有配角公式asinx+bcosx=sin(x+φ),我们称这个公式为三角函数正弦型配角公式,其中为系数,φ称为配角,配角φ由确定.但这样确定φ不直接、不直观,使用起来不方便,也容易出错.

如何使配角φ的确定变得直接、直观(也就是看到a,b就能迅速准确地确定出φ)呢?时,则

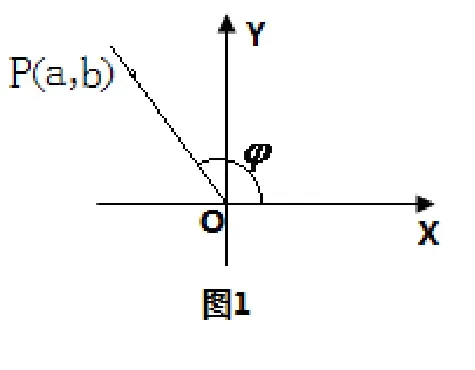
考虑到正弦、余弦的规定:当φ的终边经过点(a,b)因此,三角函数配角公式asinx+bcosx=sin(x+φ)中的配角φ的终边经过点P(a,b)(与角φ正、余弦定义一致,如图1),即为|OP|的值.

1.2 余弦型配角公式

若基于两角差的余弦公式cos(α-β)=cosαcosβ+sinαsinβ,可作以下考虑:

设asinx+bcosx=rcos(x-φ),则asinx+bcosx=r(cosxcosφ+sinxsinφ),所以a=rsinφ,b=rcosφ(其中r＞0),则a2+b2=(rsinφ)2+(rcosφ)2=r2(sin2φ+cos2φ)=r2,所以r=于是得到sinφ=

因此有配角公式asinx+bcosx=cos(x-φ),我们称这个公式为三角函数余弦型配角公式,其中为系数,φ称为配角.配角φ由确定,但这样确定的φ没有明显的意义,不能迅速准确地确定φ,必须单独计算,使用起来不方便,也容易出错.一般情况下,不用三角函数余弦型配角公式处理问题.

2 三角函数配角公式的应用

应用三角函数正弦型配角公式asinx+bcosx=sin(x+φ) 时,配角φ的终边过(a,b),我们可以迅速准确地确定一个φ或它的各个三角函数值,为我们解题带来方便.

例1化下列各式为一个角的一个三角函数的形式:

解(1)设φ的终边经过点则很容易取到一个(如图2),∴原式=

例2求下列函数的值域:

(1)y=4 sinx+3 cosx(x ∈[0,]) 的值域;(2) 求函数的值域.

解(1) 由配角公式,可设4 sinx+3 cosx=sin(x+φ),φ的终边经过点P(4,3),其中一个由可得故y=4 sinx+3 cosx,即y=5 sin(x+φ) 在区间是增函数,则当x=0 时,ymin=3;当x=时,ymax=

故函数y=4 sinx+3 cosx(x ∈[0,]) 的值域是

由配角公式,设ysinx-cosx=其中φ的终边经过点P(y,-1),则=-2y-1,即所以解得

故函数y=的值域为

例3在椭圆=1 上求一点P,使点P到直线l:3x+8y+72=0 的距离d最大.

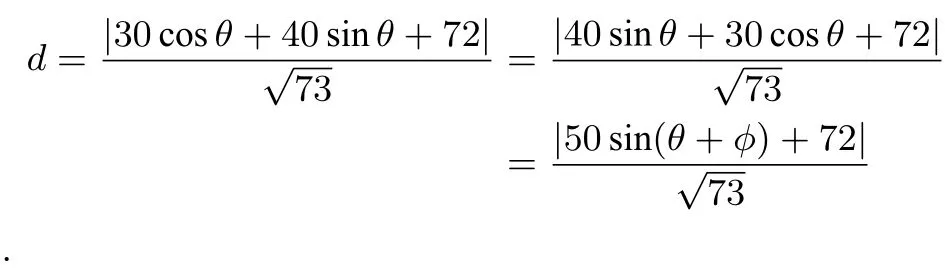
解设P(10 cosθ,5 sinθ),则40 sinθ+30 cosθ=其中φ的终边经过点(40,30),则

由(*)式易知,d最大时sin(θ+φ)=1,可得θ+φ=+2kπ(k ∈Z),即θ=-φ+2kπ(k ∈Z),则cosθ=即10 cosθ=6,5 sinθ=4.

故所求的点P为(6,4).