基于系统动力学的共享单车经济利益演化博弈研究

王梓瑜

（同济大学中德学院，上海 200092）

一、引言

在现如今共享单车如此盛行的时代，单车企业间的竞争十分激烈。基于现实情况，本文选用演化博弈论来分析竞争行为。演化博弈论由演化均衡稳定和复制动态方程构成，其中演化均衡稳定指的是系统里个体都会进行不停演化博弈，最终达到演化稳定的状态；复制动态指的是博弈主体中收益较低的主体会复制收益高的主体的策略，以此来获得更高的收益。演化博弈论在近些年得到各行业的广泛运用。2010年，易余胤在研究企业间的竞争行为时运用了演化博弈论。

系统动力学中，结构的思想至关重要，而且系统的功能也是由结构决定的，并且系统内部结构互相影响形成反馈回路。Kim（1997）、Petia（2000）等就运用系统动力学对演化博弈模型进行了简单的仿真分析，该方法已经运用到经济和管理等诸多领域。

二、演化博弈模型构建与分析

（一）演化博弈模型基本假设

1.博弈的参与方：本文假设参与者只有两个，且他们都是有限理性的。

2.行为策略：共享单车企业在此博弈中有两种策略可以选择即“降价”或“不降价”。

3.博弈策略的选择比例：在动态演化博弈中，假设共享单车企业A、B选择降价的概率分别为x、y。

4.主要参数假设及描述：RA/RB：共享单车企业A/B选择不降价时的收益；CA/CB：共享单车企业A/B选择降价时所付出的成本；MA/MB：共享单车企业A/B选择降价时带来的额外市场份额的收益；LA/LB：共享单车企业A/B不降价而B/A降价造成的市场份额丢失的损失。

（二）演化博弈模型建立及求解

假设共享单车企业A采取降价和不降价策略的期望收益分别为E1，E2，由上述条件和收益矩阵可得：

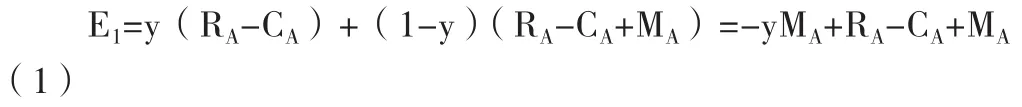
共享单车企业A采取混合策略的平均期望收益E为：

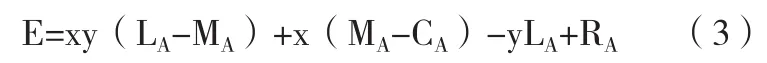
共享单车企业A的复制动态方程f（x）为：

由于A，B具有对称性，故共享单车企业B的复制动态方程f（y）为：

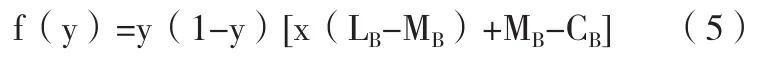
由（4）和（8）可得共享单车企业A、B组成的混合策略动态方程为：

（三）演化博弈模型稳定性分析

1.对共享单车企业A单方面策略的演化稳定分析

由于A、B具有对称性，这里以A为例。我们可以通过求出复制动态方程的稳定点来得到演化稳定策略，而该点x必须满足两个条件：f（x）=0和f’（x）〈0。

对共享单车企业A复制动态方程求导可得：

（1）当y*=（CA-MA）/（LA-MA）时，x在[0，1]上无论取任何值f（x）、f’（x）均为0，这对应着一种稳定的状态，即A可任意选择策略。

（2）当y*≠（CA-MA）/（LA-MA）时，共享单车企业A复制动态方程稳定点为x1=0，x2=1，稳定状态分析为下面两种情况：

a.当y〈y*时，f’（x1=0）〈0，故x1=0点是稳定点，即A最终不会选择降价的策略。

b.当y〉y*时，f’（x2=1）〈0，故x2=1点是稳定点，即A最终会选择降价的策略。

2.共享单车企业A、B演化稳定策略分析

由式（6）得：共享单车企业A、B雅可比矩阵为：

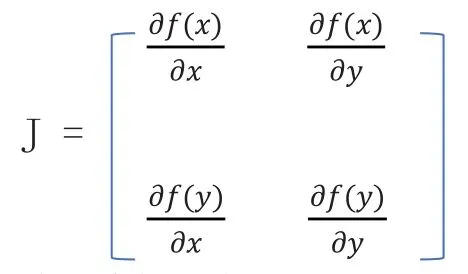
故矩阵行列式为：

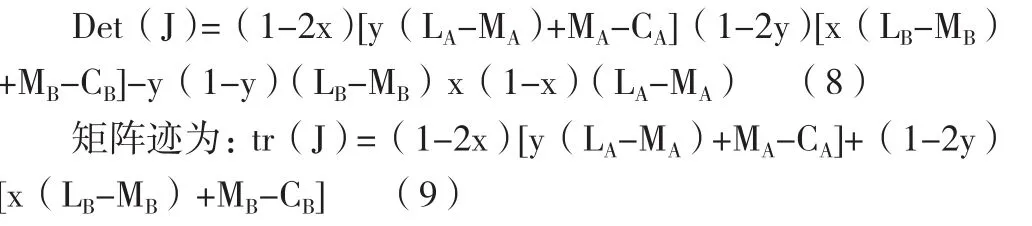
由此我们得到五个均衡点为（0，0）， （0，1） （1，0），（1，1）， [（CA-MA）/（LA-MA）， （CB-MB）/（LB-MB）]。当均衡点满足条件Det（J）〉0且tr（J）〈0时，该点就是稳定点。为了方便书写和计算，设S1= CA-MA，S2= CB-MB，S3= LA-CA，S4=LB-CB，根据雅可比矩阵分析法，分析结果如下：

（1）S1、S2、S3、S4均大于0，均衡点为（0，0）和（1，1），即A、B最终均会选择同样的降价或者不降价的策略。

（2）S1、S2、S3、S4均小于0，均衡点为（0，1）和（1，0），即A、B最终会选择一方降价另一方降价的策略。

（3）S2、S3为负值，S1、S4一正一负，均衡点为（0，1），即最终A不降价、B降价。

（4）S1、S4为负值，S2、S3一正一负，均衡点为（1，0），即最终A降价、B不降价。

三、演化博弈模型仿真分析

（一）价格演化博弈的系统动力学模型（图1）

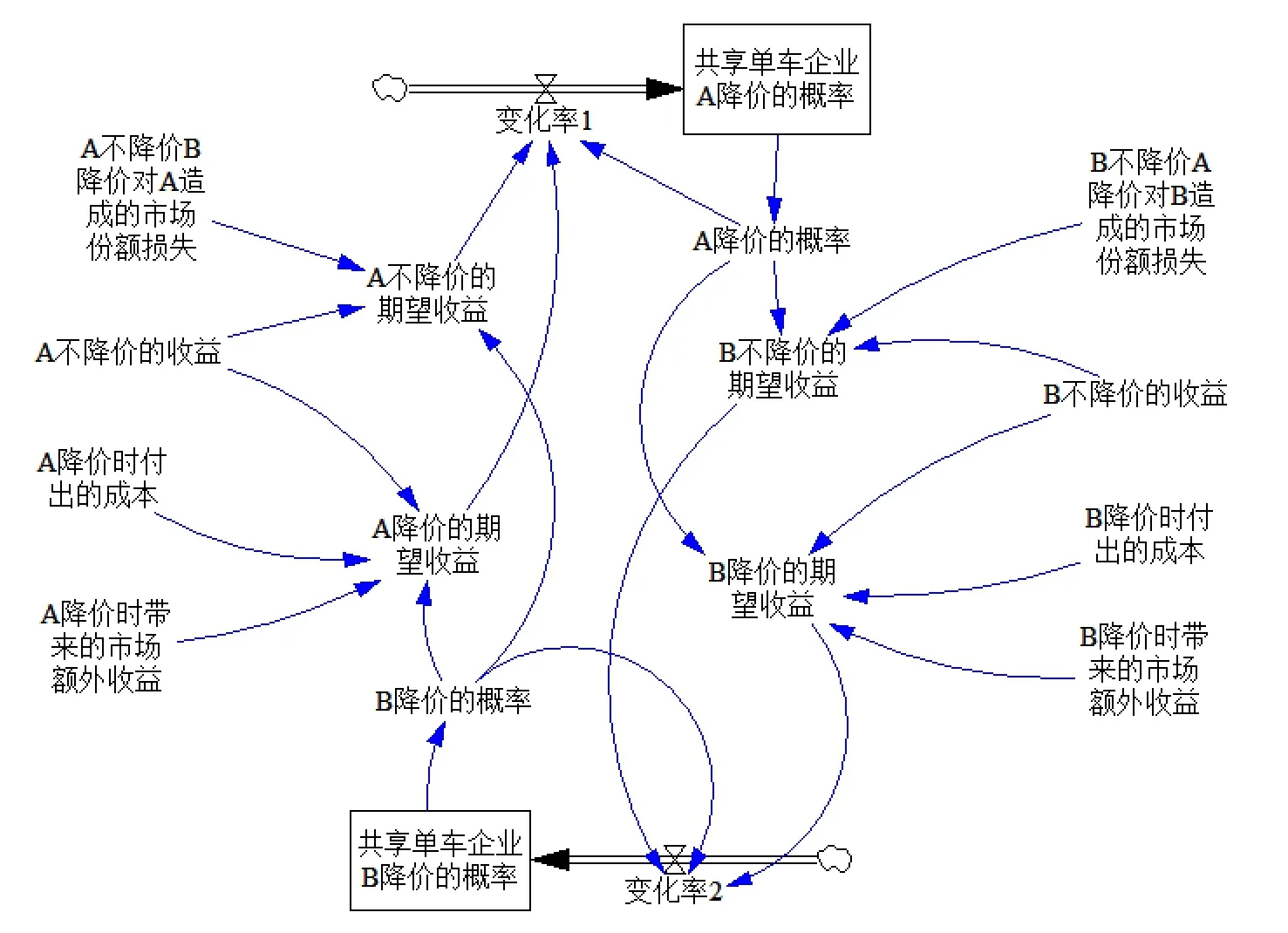
图1 价格演化博弈的系统动力学模型图

（二）系统动力学仿真方程的构建

1.S1、S2、S3、S4均大于0时，我们对参数的设置为：模拟时间为12个月，每步时常为0.5个月，LA=10， LB=13， RA=30，RB=25， CA=9， CB=8， MA=5， MB=6.5，（ x，y）的初始值分别为（0.3，0.4）和（0.7，0.6），分析结果如图2、3所示，与演化博弈模型分析一致。

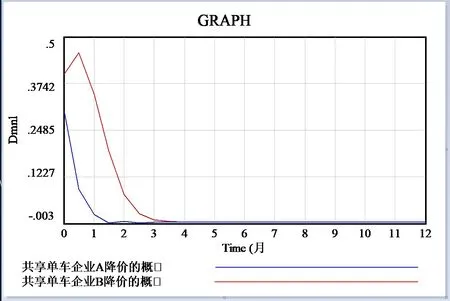
图2 系统动力学仿真模型结果

2.S1、S2、S3、S4均小于0时，时间及步骤不变，LA=5，LB=7， RA=30， RB=25， CA=9， CB=9， MA=10， MB=10.5，（ x，y）的初始值分别为（0.3，0.7）和（0.7，0.3），分析结果如图4、5所示，与演化博弈模型分析一致。

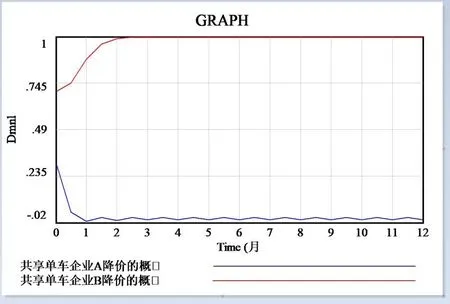
图4 系统动力学仿真模型结果

3.S2、S3为负值，S1、S4一正一负时，时间及步骤不变，LA=5， LB=10， CA=9， CB=9， MA=10， MB=10.5， RA=30， RB=25，或LA=9， LB=5， CA=10.5， CB=9， MA=10， MB=10， RA=30， RB=25，（x，y）的初始值均为（0.3， 0.7），分析结果如图6、7所示，与演化博弈模型分析一致。

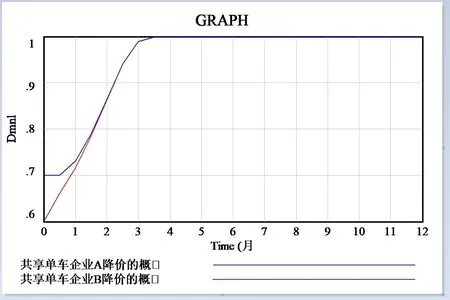
图3 系统动力学仿真模型结果

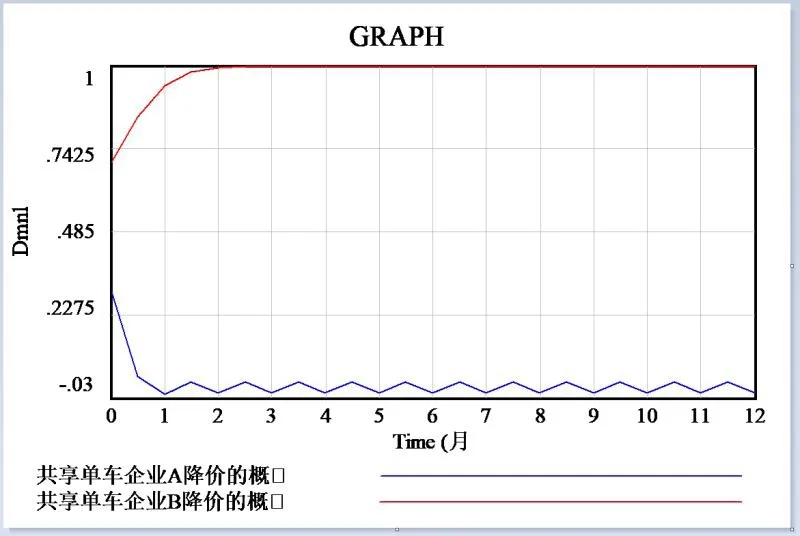
图6 系统动力学仿真模型结果

4.S1、S4为负值，S2、S3一正一负时，（x，y）的初始值为（0.7，0.3），分析结果如图8、9所示，与演化博弈模型分析一致。

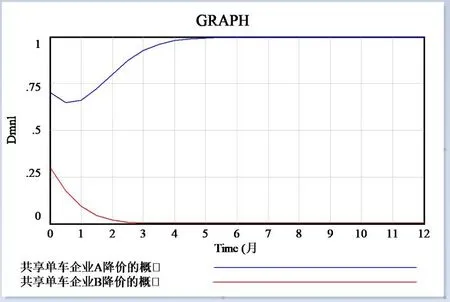
图8 系统动力学仿真模型结果

四、结论

通过上述分析，得出如下结论：

（一）价格演化博弈中，影响共享单车企业降价的因素包括降价时付出的成本、降价带来的额外市场份额收益和因对方降价自身没降价造成的市场份额损失，而不降价时的原始收益对博弈结果没有影响；

（二）数值模拟的结果显示，演化博弈的影响因素只在本企业内部而不是企业间的几个因素间进行比较来影响企业的决策，这使得演化博弈模型具有普适性，而系统动力学模型 模拟的结果很好的证明了这一点。

图5 系统动力学仿真模型结果

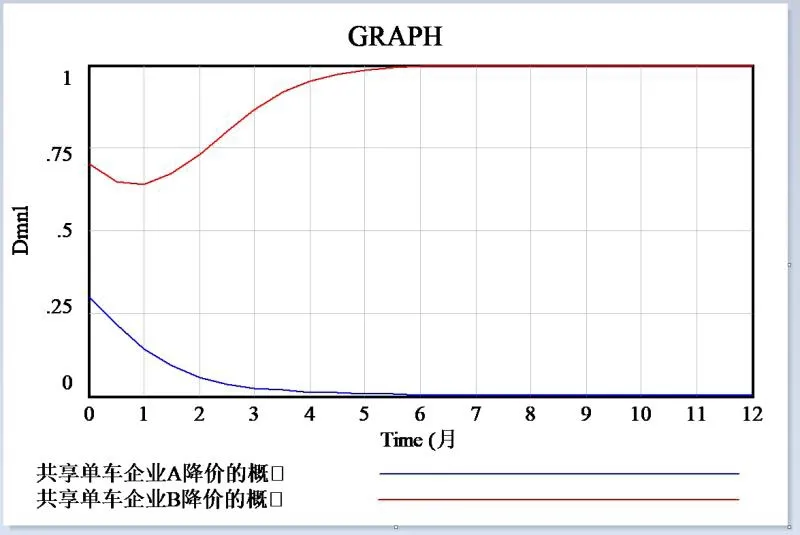
图7 系统动力学仿真模型结果

图9 系统动力学仿真模型结果