基于DE和LDU分解的结构体系可靠性分析
2020-07-21田宗睿李永华石姗姗
田宗睿,李永华,石姗姗
(大连交通大学 机车车辆工程学院,辽宁 大连 116028)*
在结构可靠性分析与设计中,可靠性一直是衡量结构功能效用的重要依据,贯穿于结构产品的全寿命周期过程中.但是,由于结构自身设计的影响及在工作状态下随时遇到的不确定因素,在实际工程设计中,结构体系出现破坏的情况时有发生.为了提高结构体系的可靠性与安全性,使其满足实际工程要求,有必要对结构体系进行可靠性分析.
一般的可靠性分析方法只针对一个失效模式的情况,但结构体系的失效模式却很多,对其可靠性的研究较为困难,由此产生的问题一直是可靠性领域研究关注的热点.结构体系传统的可靠性分析方法有一阶界限法、二阶界限法、概率网络估算法和蒙特卡洛法[1]等.近年很多学者对此有了新的研究成果,李正良[2]等提出了一种基于自适应点估计和最大熵原理的结构体系多构件可靠度分析方法,该法所得结果精度满足工程要求.Marco N.Coccon等[3]提出了一种海上结构体系可靠性分析方法,此法充分考虑部件和失效模式之间的统计相关性,适用于海上结构的风险评估.Ruixing Wang等[4]针对线性结构系统,提出了一种基于体积比理论的非概率可靠度计算方法,能够有效减少计算量和公式推导的步骤.彭伟等[5]通过构造Copula函数来分析两部件系统的失效相关性,能够更好地描述所有部件的失效特性.李洪伟[6]等利用近似数值分析法建立共因失效的结构系统可靠性模型,在保证计算精度的前提下提高了求解效率.周金宇[7]等利用阿基米德族的Clayton Copula函数建立串并联结构系统的疲劳可靠性模型,为疲劳寿命预测与可靠性设计提供新方法.安宗文[8]等考虑齿轮的两种失效模式,将二元正态分布函数引入到可靠度求解过程中,为齿轮可靠性的研究方法提供了新途径.涂宏茂[9]等提出了基于一次二阶矩法近似的系统可靠性分析方法,能够获得效率较高且较准确的计算结果.
为了进一步提高结构体系可靠度的计算精度与效率,本文提出了基于DE算法和LDU分解的结构体系可靠性分析方法.此法将DE算法和LDU分解相结合,充分DE算法不易陷入局部最优和LDU分解计算准确的特点,使计算结果更精确.通过实际算例验证方法的可行性与有效性.
1 DE算法与LDU分解的基本原理
1.1 可靠性指标的几何意义及优化模型
结构的极限状态是结构在达到破坏前的临界状态,用 Z=g(X1,X2,…,Xn) 表示[10],其中 X1,X2,…,Xn是结构中的n个任意分布的独立随机变量.对于非正态随机变量利用R-F法(Reckwitz-Fiessler法)将其当量正态化[11],能够得到当量正态化后变量的均值μ′Xi与方差σ′Xi.
可靠性指标的几何意义旨在标准正态空间中坐标原点到极限状态超曲面的最短距离.由此建立最优化数学模型,其表达式为:
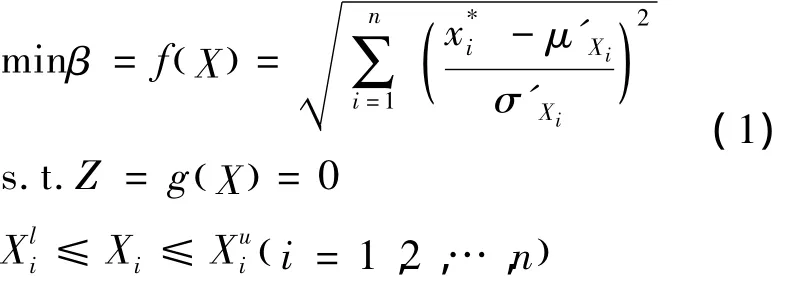
式中,可靠性指标为β,功能函数为Z,极限状态超曲面上的点为,随机变量为Xi,随机变量上限为,下限为.利用罚函数法,将式(1)转换为无约束优化模型:

式中,M为惩罚因子,对应的项为惩罚项.
1.2 DE算法基本原理
DE算法[12-13]是Storn等人于1995年提出,此法能求解具有高度非线性特征的连续函数的极小值.DE算法的原理虽与遗传算法相似,但其能够在变异操作中使用差分策略,避免了遗传算法中变异操作的不足,具有较好逼近效果.
DE算法的基本思想是:首先由当前个体通过变异操作生成新一代个体,成为变异个体;再将当前个体与新一代个体进行混合交叉操作,生成试验个体;然后通过选择操作,将试验个体与当前个体进行比较,选择最优个体实现进化.该法主要包括种群初始化、变异、交叉和选择操作[13].
1.3 LDU分解的基本原理
LDU分解作为矩阵三角分解的一种,对于常系数线性方程组的求解较为适用[14],广泛应用于动态无功优化、潮流计算等电力系统计算方面[15].LDU分解能够将具有相关性的变量转换为相互独立的变量,对于处理具有相关性的函数和变量具有较大优势.在结构体系可靠度的计算过程中,主要用于处理相关失效模式间的相关系数矩阵,使各失效模式具有相互独立的特征.
设A=(aij)是n阶矩阵,如果A可分解成A=LDU,其中L为单位下三角矩阵,D为对角矩阵,D=diag(d1,d2,…,dn),di> 0(i=1,2,…,n),U为L的转置,则称A可作LDU分解.
LDU分解的充要条件是当且仅当A的顺序主子式 Δk≠ 0(k=1,2,…,n-1 )时,A可唯一地分解为LDU.LDU分解表达式为:
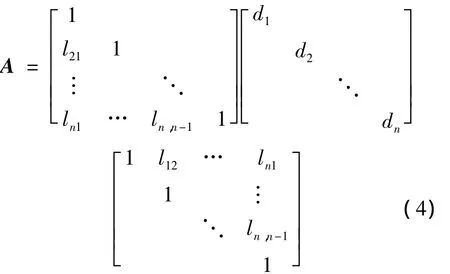
式中,三个矩阵均为n阶方阵,i为行数,j为列数,lij为矩阵中的数值元素,dn为D中对角线上的数值元素.
2 结构体系失效概率的求解
结构体系可分为串联、并联和混联体系.混联体系可转换为全串联或全并联体系.无论该结构属于哪种结构体系,在可靠度的求解过程中均需要计算多失效模式的联合失效概率,其表达式为:

式中,β为可靠性指标矩阵,ρ为相关系数矩阵,Zi为功能函数.
由式(5)可知,可靠性指标和相关系数矩阵共同影响结构体系失效概率.相关系数矩阵表示为:

式中,gk(X)为功能函数,σ为其标准差,Cov( gi( X ),gj( X ) )为失效模式间的协方差矩阵,α为灵敏度系数矩阵,表示标准正态空间内的验算点矩阵.
根据可靠性指标与相关系数矩阵的计算结果,可将多失效模式的联合失效概率的求解转化为多维正态积分的计算,进而计算体系可靠度.利用LDU分解的思想,将相关的标准正态随机变量转换为互不相关的正态随机变量.根据文献[16]的证明思路,对自变量x连续进行两次线性变换,将积分上限值β代入,最终可得β″=D-1/2L-1β.利用LDU分解,通过对自变量进行两次线性变换后,多维标准正态分布函数的Φ(β,ρ)可表示为:

式中,β″= (β″1,β″2,…,β″n)T,Φ(·)为标准正态分布函数.
综上所述,基于DE和LDU分解的结构体系可靠性分析流程如图1所示.
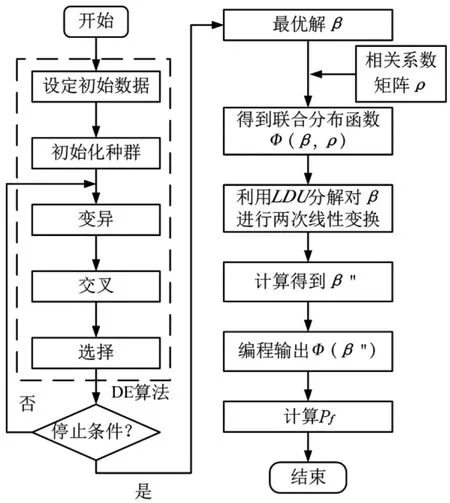
图1 基于DE和LDU分解的结构体系可靠性分析流程
3 算例分析
3.1 算例1
假设某串联体系包含两个失效模式,对应的功能函数分别为:
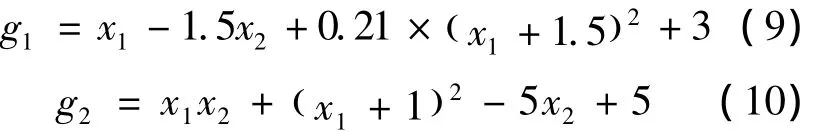
式中,x1与x2均服从标准正态分布N(0,1),且相互独立.
根据式(2)和式(3),分别建立各功能函数对应的优化模型:

通过求解两个优化模型,失效模式对应的可靠性指标结果见表1.

表1 可靠性指标值
根据式(6)和式(7),两个失效模式的功能函数间的相关系数为ρ=0.959 3,根据式(8)可得多失效模式的联合失效概率表达式为:

式中,Pf1,2为两失效模式的联合失效概率.
该串联结构体系的可靠度计算表达式为:
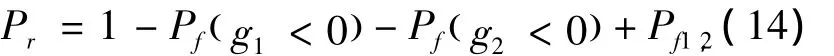
式中,Pr为可靠度.
分别利用本文方法和100 000次蒙特卡洛仿真计算该结构体系的可靠度,结果见表2.
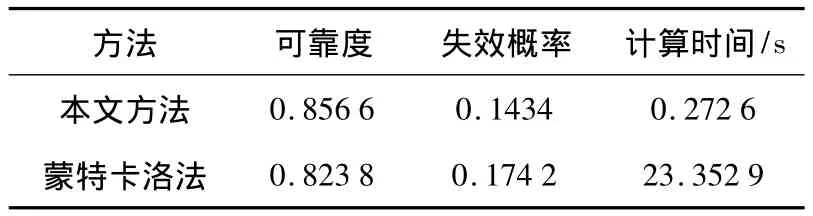
表2 可靠度结果
结果分析对比表明,此法与蒙特卡洛法结果相近,但速度快于蒙特卡洛法,证明了该法的有效性.
3.2 算例2
由于抗侧滚扭杆长期承受较大扭矩,其结构安全与否对行车安全有着重大影响[17].为进一步验证此法的有效性,以某动车组的抗侧滚扭杆为研究对象,对其进行可靠性分析.抗侧滚扭杆安装在转向架的构架上,由扭杆轴、扭转臂和连杆构成,其中扭杆轴与扭转臂的连接方式为过盈配合,连杆与扭转臂采用螺栓连接.抗侧滚扭杆的几何模型如图2所示.

图2 抗侧滚扭杆几何模型

图3 抗侧滚扭杆的受力示意图
车体通过连杆上的橡胶节点将力由连杆,经过扭转臂传递到扭杆轴,进而在扭杆轴上产生扭矩.由于扭杆轴具有良好的回弹特性,能够有效抵消车体上传来的扭转作用,以满足抗侧滚要求.抗侧滚扭杆的受力示意图如图3所示.
抗侧滚扭杆可能存在的失效模式有弯曲强度失效、扭转强度失效和弯扭组合失效,这些失效模式共同影响,抗侧滚扭杆结构体系的可靠性.扭杆轴材料的许用剪切应力[τ]为700 MPa,抗拉极限[ σb]为1 450 MPa,屈服极限[σs]为 1300MPa,载荷P(N)服从正态分布N(35 000,50),扭杆轴直径d(mm)服从正态分布N(35,3),并且P与d相互独立.现求解该抗侧滚扭杆的可靠度.
当结构发生扭转失效时,其功能函数表达式为:

式中,Tmax为最大扭矩,Wp为抗扭截面系数,扭转臂l为240 mm.
当结构发生弯曲失效时,其功能函数表达式为:
式中,Mmax为最大弯矩,Wz为抗弯截面系数,a为110 mm.
弯曲与扭转组合失效的功能函数表达式为:

根据式(2)和(3)建立可靠性指标求解的优化模型,扭转失效的优化模型为式(22),弯曲失效的优化模型为式(23),弯扭组合失效的优化模型为式(24).
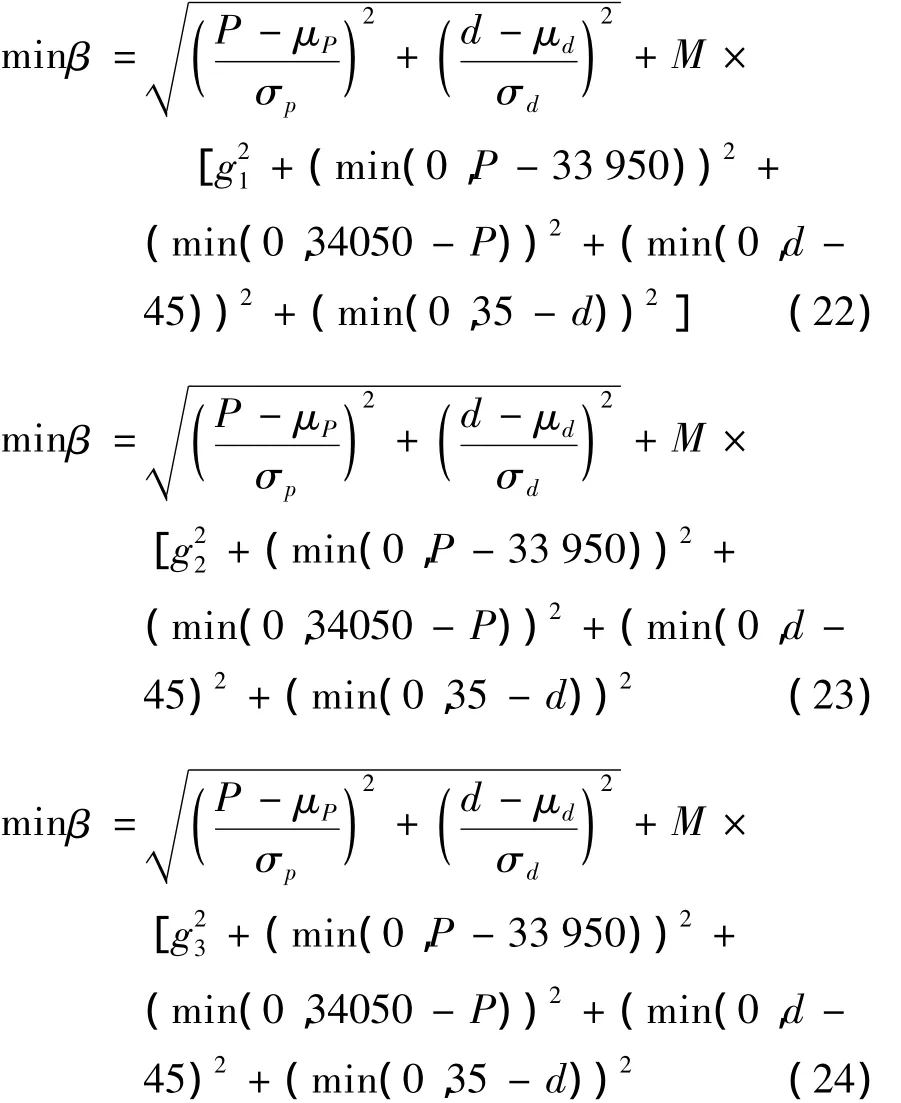
式中,μP为载荷的均值,σp为载荷的标准差,μd为直径的均值,σd为直径的标准差.
利用DE算法求解三个功能函数的可靠性指标,计算结果见表3.
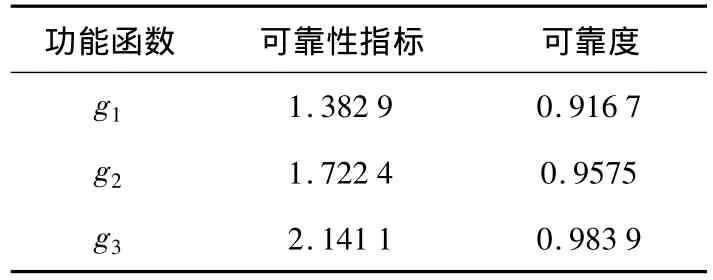
表3 各失效模式可靠度
根据式(6)和式(7),该结构体系各失效模式间的相关系数矩阵表达式为:

抗侧滚扭杆的三个失效模式共同组成串联结构体系,利用LDU分解处理相关系数矩阵,根据式(8)可得多失效模式的联合失效概率表达式分别为:

式中,Pf1,2为 g1和 g2的联合失效概率,Pf1,3为 g1和g3的联合失效概率,Pf2,3为g2和g3的联合失效概率,Pf1,2,3为 g1、g2和 g3的联合失效概率.
抗侧滚扭杆的可靠度计算表达式为:
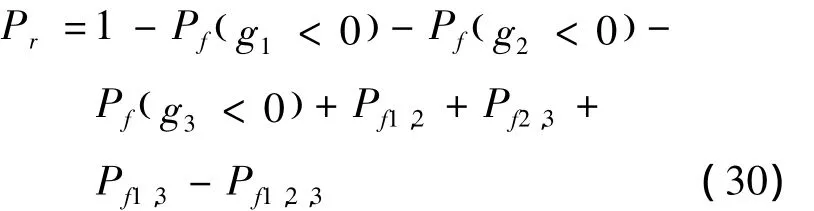
式中,Pr为可靠度.
利用本文方法和100 000次蒙特卡洛仿真求解该结构体系的可靠度,结果见表4.
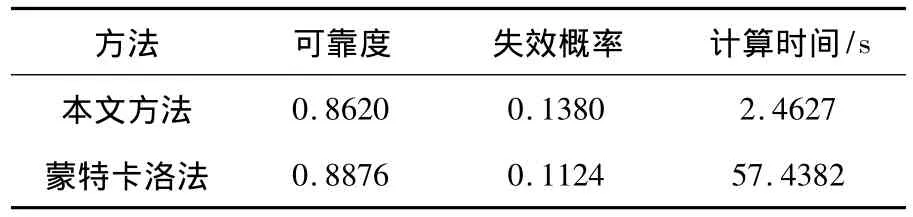
表4 可靠度计算结果
由表3可知,扭转失效的可靠性指标为1.382 9,弯曲失效的可靠性指标为1.722 4,弯扭组合失效的可靠性指标为2.141 1;由表4可知,抗侧滚扭杆的可靠度为0.862 0,与蒙特卡洛法结果相近,证明本文方法的求解精度满足要求.同时表明本文方法切实可行.
4 结论
(1)将DE算法引入到可靠性指标的求解过程中,所得结果准确性较高,由于不受函数非线性的影响,增强了可靠度求解的精度;
(2)将LDU分解引入到结构体系可靠度的计算中,可有效提高结构体系可靠度的计算精度,并且减少了计算量,为结构体系可靠度的求解提供了新的途径;
(3)通过对解析算例和工程算例的计算验证了该方法求解的精度和速度,同时说明了此法适用于复杂结构体系的可靠性分析.
