基于动力学理论的轨道车辆设备安装弹性元件参数设计及应用

刘春艳，滕万秀

(中车长春轨道客车股份有限公司 国家轨道客车工程研究中心，吉林 长春 130062)*

因高速动车组采用了动力分散技术，故需在不同的车体下面吊挂质量较大的变压及变流等大质量设备.在高速动车组运营过程中，对车下设备进行跟踪测试时发现其振动加速度较大，该振动加速度一旦传给车体，势必对车辆的运行平稳性产生不好的影响.

在产品设计中，对于大质量的设备采用了弹性元件作为吊装隔振件安装设备与车体之间，利用弹性元件减弱设备的振动传递给车体，但如何设计该弹性元件的刚度使其发挥更好的作用，很多科研院所从理论及工程应用方面均进行了大量的研究.同济大学宫岛、周劲松等人［1］对高速动车组下设备对车体振动传递与模态频率的影响机理进行了研究，详细地阐述了车体模态频率数值的计算方法，同时对振动传递特性和模态频率跳变现象进行论述;同济大学夏张辉、周劲松等人［2］针对高速动车组车下设备悬挂系统的解耦优化设计方法提出了正向解耦和逆向解耦的两种方法;罗光兵、曾京等人［3］也提出，车下设备采用弹性悬挂吊装方式能够优先减低车体的弹性振动，在故障工况下也不会恶化车体的振动;西南交通大学的石怀龙［4］采用动力学吸振原理对动车组的车下设备的悬挂元件参数进行了设计与研究，可在产品设计中，有些设备的悬挂参数设计易采用隔振理论较为合适.本文结合实际的研发产品，对多种类型的设备悬挂参数进行设计，根据设备特点结合隔振理论和动力吸振理论的使用原则，对设备安装弹性元件的参数进行合理设计.

1 常用设备吊弹性元件及工作原理

在以往的产品设计中，设备的弹性吊装件常用以下几种类型，图1所示.

楔形减振器和锥形减振器内部均封装了橡胶，对橡胶性能进行前期设计，保证形成产品后，整个产品刚度可控，孙玮光、石芳、刘晓雪等人［4］结合有限元仿真和试验手段对动车组车下吊装设备用橡胶减振器如何研制进行了阐述.

分体式减振器一般有两个独立的弹性元件组成.在车辆装配大型设备时，将选定好的减振器安装在设备吊座与车体之间，用于衰减设备振动传递给车体.

图1 常见设备吊弹性元件形式

分体式减振器结构相对复杂，但假设上、下弹性元件的刚度和静挠度分别为 k1、k2和 δ1、δ2，根据线性振动理论中弹簧串联的概念，则整个弹性吊装结构的综合刚度k和位移δ也表示为式(1)和式(2):

分体式弹性吊装结构特点:

通过合理分配上、下两个弹性元件的刚度，可使弹性吊装结构具有较小的综合刚度，解决单个弹性元件不能提供足够小刚度的问题.

由于刚度串联效应，每个弹性橡胶元件刚度可以取得大些，一是便于工程实现，二是动态位移越小则有助于保证橡胶件使用寿命.

通过优化上、下两个弹性元件各自刚度，可提供较大变化范围的综合刚度，为整车动力学参数优化提供更大的参数选择空间.

对于大质量设备而言，通过采用多个分体式弹性吊装结构，可均匀分配各处吊挂点的负荷，使设备作用在车体上的载荷分布更加均匀.

2 弹性元件参数设计方法

2.1 基于隔振理论设备吊挂刚度设计

从隔振理论角度出发，车下设备悬吊在车体底架上，轮轨激扰由车体传递至设备，可依据隔振理论进行设备悬挂频率设计，以降低设备的振动.同样可根据隔振原理对悬挂参数进行设计，以隔离设备本体的高频激励向车体的传递.对于高速动车组车下设备而言，大部分存在一定的自身振动源，重点需要隔离设备自身振动向车体的传递，减小车体的高频振动，提高乘坐性能.

设激扰频率ω与减振体固有频率ωn之比为g，其中ωn=，k为弹性联接元件刚度，m为隔振对象质量;已知单自由度系统的绝对隔振传递率表达式为:

图2为绝对传递率，为降低隔振对象振动水平，其固有频率低于基础激振频率1/时隔振系统才具有隔振能力，而且频率比相差越大，系统隔振能力越强，即应保证弹性联接元件足够软.弹性元件的阻尼作用可减小共振区的振动幅值，但会增加高频振动的传递.当基础激扰为广谱时，合适的阻尼比可以抑制共振响应幅值，也不至于使高频振动过大，应综合考虑阻尼比选取.

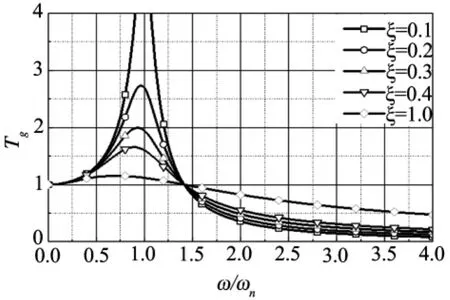
图2 单自由度消极隔振系统绝对传递率

2.2 基于吸振理论设备吊挂刚度设计

弹性系统动力吸振问题是由弹性体和离散质量构成的刚柔耦合动力学系统，需要联立求解偏微分方程和常微分方程.首先，需要计算弹性体的模态信息，会用到模态分析、模态截断和模态综合法;其次，采用离散振动系统幅频特性分析方法，组装系统微分方程并推导出目标量对输入量的传递函数，从而进行传递率分析，最终获取吸振器的最优悬挂参数.对于均直弹性梁的动力吸振问题，若只考虑第一阶模态，则就相当于求解主质量受到简谐激扰力时的动力吸振问题，若将吸振器安装在弹性梁振幅最大位置，则主质量M最小，相对于确定的吸振器质量m，可获得最大的吸振器和主质量的质量比u=m/M，从而可得最佳吸振效果.

一般车体一阶垂向弯曲模态对车体弹性需要重点关注，基于车体在整备(不含转向架)但不包含车下设备时的一阶垂弯模态频率，可据此计算出基于动力吸振理论的车下悬挂设备的最优固有频率范围.

基于无阻尼单自由度系统固有频率计算方法，得到设备固有频率计算公式为:

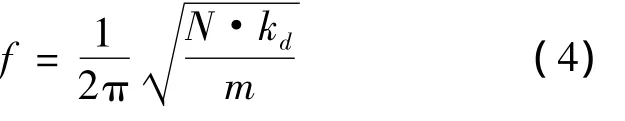
则可推导出动刚度表达式为kd=，则各吊挂点平均静刚度和静挠度为:

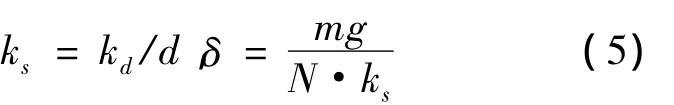
式中，N为吊挂点数目;kd为吊挂点平均动刚度;ks为吊挂点平均静刚度;δ为吊挂点平均静挠度;g为重力常数;d为动静刚度比(该值假定1.45).

本文以采用弹性设备吊挂方式的某高速动车组为例，阐述弹性元件参数在车辆系统中的设计过程.

3 工程应用实例

3.1 车辆基本参数

该动车组车辆车下共五个悬挂设备，车辆的基本参数见表1，设备具体位置见表2所示.

表1 车辆基本参数

表2 车下设备具体位置汇总

其中污物箱质量较轻，为了连接的有效性，采用刚性连接.

同时有限元计算得出车辆在无车下吊挂设备的整备状态下一阶垂向弯曲固有频率为10.56 Hz，如图3所示，该值作为车下悬挂设备设计频率的匹配基础数据.

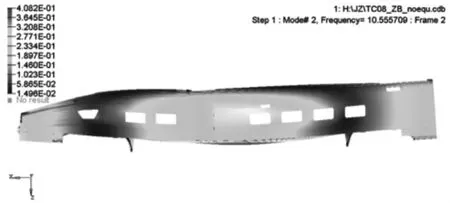
图3 车下设备的整备状态车辆一阶垂向弯曲固有频率

3.2 设备吊挂参数设计

该高速动车组车下废排风缸设备为有激扰源，设备自身的振动比较剧烈，为此需要采用积极隔振来隔离设备向车体的振动传递，减小车体的高频强迫振动.根据积极隔振理论，从悬挂力的传递率角度来说，为了减小振动向基础的传递，减振体的固有频率需要小于激振频率的1/，这就要减振体悬挂足够软.

由于废排风机工作频率为30 Hz，故车下设备的悬吊频率应该满足:

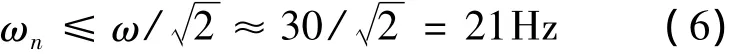
设备悬吊频率越是远离有源振动频率，积极隔振效果越好.

结合现有弹性元件类型及设计空间，确定废排风缸的悬挂元件选用锥形减振器，刚度为133 N/mm，频率为7 Hz.

根据弹性梁的质量减振理论设计出车下各设备的固有悬挂频率即吊挂刚度.本节基于弹性吸振器原理设计吊挂刚度时，根据设备的特点，对蓄电池、充电机和制动控制模块进行设计，采用章节2.2中的式(4)、式(5)进行参数计算.表3为基于动力吸振理论的车下设备悬挂频率计算值，表4为对应的吊挂刚度、静挠度计算值.

表3 基于动力吸振理论的车设备悬挂频率设计

表4 车下设备吊挂刚度理论计算值

3.3 车辆平稳性分析

采用动力学分析软件SIMPACK创建车辆刚柔耦合动力学模型，将上述确定的不同悬挂元件的参数设置到动力学模型中［6］，见图4所示.

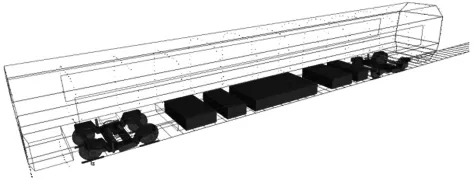
图4 含设备悬挂元件刚度的动力学分析模型

根据GB5599-85标准［7］进行车辆运行平稳性分析，运行平稳性指标如式(8)计算:

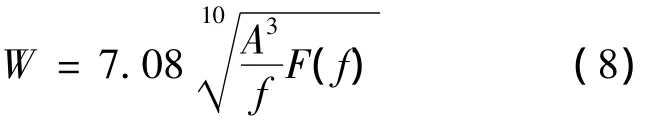
式中:W为平稳性指标;A为振动加速度，g;F为振动频率，Hz;F(f)为频率修正系数，见表5.

依据平稳性指标确定车辆运行平稳性的等级列于表6，垂向和横向采用相同的评定等级.根据标准规定加速度测点选在1位或2位端转向架上方距车体中心1 m车体地板面上.新造车辆平稳性指标不应高于2.5.

表5 平稳性指标频域加权值

表6 平稳性指标等级

设置车辆运行速度为350 km/h，采用我国秦皇岛到沈阳的实测高速轨道不平顺激励谱，其车辆运行平稳性结果见表7所示.

表7 车辆平稳性计算结果

3.4 整备状态车辆模态分析

将确定的不同悬挂元件的参数创建在车体有限元模型中，进行车下设备弹性吊挂车体整备模态分析.分析结果发现，与刚性吊挂相比，采用设计后的弹性吊挂可使车体一阶垂弯频率从9.36 Hz提升至11.81 Hz，见图5所示.

图5 不同悬挂元件的车体一阶垂向弯曲频率

4 结论

(1)在进行车下设备悬挂刚度设计时，建议有源设备的吊挂刚度基于隔振理论设计，要求吊挂刚度足够软，以避免设备振动向车体的传递;无源大质量设备吊挂刚度基于动力吸振理论设计，有助于抑制车体的弹性振动;

(2)根据设备特点利用隔振理论与动力吸振理论，确定废排风缸的设计频率为7 Hz，静刚度为133 N/mm;蓄电池的设计频率为9.18 Hz，静刚度为1 530 N/mm;充电机的设计频率为10.45 Hz，静刚度为1040 N/mm;制动控制模块的设计频率为10.56 Hz，静刚度为710 N/mm;

(3)对设计后的设备弹性元件，通过创建刚柔耦合的动力学模型进行平稳性分析，得出车辆的横向平稳性和垂向平稳性均小于2.5，满足GB5599-85的要求;

(4)与刚性吊挂相比，采用设计后的弹性吊挂可使车体一阶垂弯频率提高26%.