基于Anylogic的转向架生产工艺仿真及评价

2020-07-21黄晋陈文杰姬帆郭瑞军马思群霍宗达

大连交通大学学报 2020年4期

黄晋，陈文杰，姬帆，郭瑞军，马思群，霍宗达

(1.中车大连机车车辆有限公司，辽宁大连 116022;2.大连交通大学交通运输工程学院，辽宁大连 116028)*

铁路机车转向架是机车车辆组中最为重要的部件之一，它具有支撑车体、转向、制动等功能.但是转向架生产流程极其复杂生产耗时也较长，企业在实际的生产过程中面临了很多的问题，造成了一些不必要的浪费.

目前，国内生产系统工艺流程的仿真主要结合了 eM-Plant、Flexsim、Petri网以及 SLP方法进行研究.郭全杰［1］对铝合金门窗混流生产系统现状进行了分析，在eM-Plant软件中建立了仿真模型，对门窗混流生产系统的延时性、生产线平衡性、瓶颈、物流运送系统等进行分析优化，并提出了改进建议.Moghadam和Karimi等人［2］将离散系统仿真(DES)与多标准决策分析(MCDA)结合，在汽车供应链中将制造过程与物流活动集成研究，提出了较优的改进方案.Serguei［3］讨论了复杂离散生产系统建模的分布式决策的结构及过程控制方法.Wang［4］提出运用线性规划方法对离散生产系统的生产计划进行优化的解决方案.

本文介绍了生产管理的相关理论，提出了设备忙闲率评价的相关计算公式，主要从工期计算、仿真运行以及工艺流程评价三个角度出发，对机车的转向架生产加工进行评价，然后基于Anylogic软件对机车转向架的生产进行仿真，并针对具体存在的问题提出解决方法.

1 生产工艺及工期计算理论

1.1 产品的生产周期

1.1.1 单件产品生产周期

单件结构简单的产品，生产周期为该产品在各个工艺阶段生产周期的总和.本文提出平行工序计算，即在完成第一日零部件的需求数量加工后，各工序即可形成平行工序分段生产，每个工序分段的产品作为第二日下一个工序分段的物料，统计工序分段的总数，即为单件产品的生产周期，也称工期(单位，天).如图1所示.

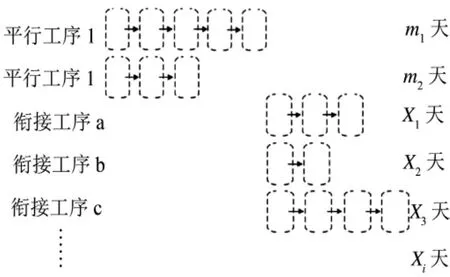
图1 单件产品工期计算方法

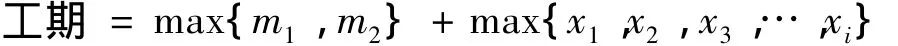
平行工序间独立进行生产，衔接工序与平行工序顺序完成产品生产，其和值为对应加工周期;max{}为各分阶段衔接工序内的最大天数.

1.1.2 成批产品生产周期

成批产品的生产周期的计算原理与单件产品生产周期基本相同，不同之处在于要考虑零件和产品在制造过程中的移动方式.移动方式不同，生产周期的长短也不同.成批产品在三种移动方式下的加工周期计算如下.

平行移动方式是一批零件中的每个零件在前一道工序完工后，立即传送到下一道工序继续加工.平行移动方式下加工周期的计算公式如(1)所示.

其中，T1代表一批零件平行移动的加工周期，m代表零件加工工序数目，n代表零件批量，tmax代表各道工序中最长工序的单件时间.

顺序移动方式是指每批制品在上一道工序加工完毕后，整批地移送到下一道工序进行加工的移动方式.顺序移动方式下加工周期的计算公式如(2)所示.

其中，T2代表一批零件顺序移动的加工周期，ti代表第i道工序的加工时间.

平行顺序移动方式是顺序移动方式和平行移动方式两种方式的结合使用.是指一批零件在一道工序上尚未全部加工完毕，就将已加工好的一部分零件转入下道工序加工，以恰好能使下道工序连续地全部加工完该批零件为条件的移动方式.平行顺序移动方式下加工周期的计算如式(3)所示.

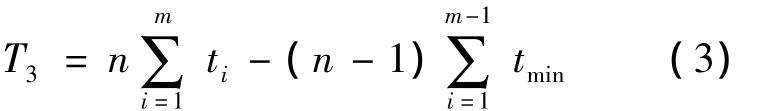
其中，T3代表一批零件平行顺序移动法下的加工周期，tmin代表较短工序，是指某一道工序的单件加工时间比前道工序短，或比后道工序短.

平行移动方式的加工周期短，在制品占用量少，但是产品运输次数多.顺序移动方式的加工集中，减少设备调整时间和运输工作量，但是有等待加工和等待运输的现象，产品生产周期长.平行顺序移动方式在劳动过程中中断时间比顺序移动方式的少，零件生产周期较短.但是组织管理比较复杂.

1.2 生产线平衡和瓶颈工序

生产线平衡是指合理安排生产线上每个装配工序或加工工序，保证在每道工序的作业时间大致相同，以便实现一个流的加工生产，生产线的平衡问题也称为工序同期化问题.

生产线平衡可以缩短产品装配时间，增加单位时间的产量，降低生产成本.减少工序间的在制品及其准备时间，减少场地的占用，从而缩短生产周期.瓶颈工序是指生产流程中节拍最慢的工序，即限制整条生产线产能的工序.瓶颈工序的产能小于或等于整条生产线的产能，应该充分发挥瓶颈工序的产能效率，提高生产线的产出.

2 生产工艺的评价方法

本文从设备忙闲率、在制品存放区的存放比例、生产瓶颈角度出发对整个生产流程进行仿真分析.

2.1 设备忙闲率

为更有效评价工艺流程中各工序和设备的工作状态，提出仿真忙闲率、仿真平均忙闲率、理论平均忙闲率、忙闲率误差等评价指标.现对各个评价指标做出解释.

仿真忙闲率，指某时刻仿真的设备忙闲比例，实质是该类设备工作的数量与总设备数量的比值.按不同仿真软件的仿真间隔时间，可取单位时间，如1 min.

仿真平均忙闲率，指仿真统计的该设备在班制时间内的忙闲率的均值.

理论平均忙闲率，指在一定的班制时间内，工艺流程中设备加工一定数量的产品所耗费时间与总班制时间的比值.即为生产时间与总时长的比值.其中生产时间是单件产品加工时间与加工件数的乘积.

忙闲率误差，指理论平均忙闲率与仿真平均忙闲率差值的绝对值，用来衡量设备及工艺流程仿真的准确性.

对于时刻的设备仿真忙闲率、仿真平均忙闲率、理论平均忙闲率、忙闲率误差的计算公式如(4)～(7)所示:

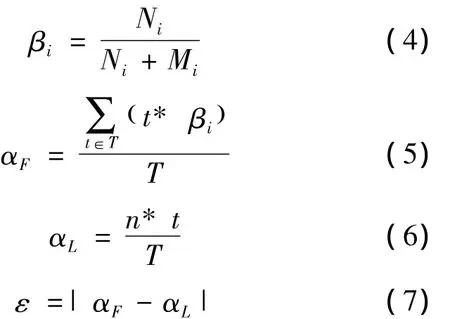
其中，βi代表i时刻的设备仿真忙闲率，Ni代表工作设备数量，Mi代表未工作设备数量，αF代表仿真平均忙闲率，t代表单个工序加工时间，T代表加工总时长，αL代表理论平均忙闲率，ε代表忙闲率的仿真误差.

时长指该设备处于一定仿真忙闲率状态的持续时间.T指该设备所处工艺流程的班制时间，如两班倒为15 h.

忙闲率误差即理论平均忙闲率与仿真平均忙闲率差值的绝对值，该值越小说明仿真结果越准确，一般不超过10%时可检验仿真结果的可靠性.

2.2 在制品存放比例

在制品存放区可以有效地避免设备间物料的堵塞.但是在制品存放区如果设置不合理，会占用车间场地，导致生产系统物流的不顺畅，给企业带来更高的附加成本，从而影响企业的效益.

存放比例可以表示存放区的利用效率.存放比例为存放区已放置产品的个数与存放区存放容量的比值，一般可用最大存放比例表示存放区域的利用率.

在生产过程中，存放区存放比例在60%～100%之间.存放比例过高会造成堵塞，影响下一步生产，存放比例过低则会造成资源的浪费.

2.3 生产瓶颈分析

生产瓶颈往往出现在那些生产能力小于需求能力的加工设备上，瓶颈设备往往是决定系统生产能力的关键.提高设备利用率，优化生产流程和资源配置的主要问题就是识别瓶颈设备并扩大瓶颈设备的加工能力.要消除生产系统的瓶颈问题首先要确定瓶颈环节的位置，现阶段识别生产瓶颈的方法主要有设备负荷率分析法、物流量分析法、节拍分析法、基于仿真的瓶颈分析等.本文主要应用Anylogic软件进行瓶颈分析.

3 转向架生产周期的计算实例

3.1 转向架生产计划

某机车厂主要生产四种类型的转向架产品:城轨机车转向架、动车转向架、内燃机车转向架、电力机车转向架.机车厂从市场需求出发来组装产品，借此拉动工序的零部件加工，是拉式生产方式.在整个转向架的生产过程中，车轮和车轴是生产各种型号转向架产品的关键部件，是两条独立的生产线.转向架生产线是混流生产.

机车厂根据产品订单，做出了相应的生产计划.对于最大日产量和基本日产量均有两个方案，分别为:

方案1:最大日产量，每天生产3台城轨机车转向架、2台动车机车转向架、1台内燃机车转向架.

方案2:最大日产量，每天生产3台城轨机车转向架、2台电力机车转向架、1台内燃机车转向架.

方案3:基本日产量，每天生产2台城轨机车转向架、1台动车机车转向架、1台内燃机车转向架.

方案4:基本日产量，每天生产2台城轨机车转向架、1台电力机车转向架、1台内燃机车转向架.

表1是在不同生产计划下产品主要部件的需求量及生产过程中各在制品的产量.由表1可以看出机车厂产品数量较大，一年中分批地制造相同的产品，是成批生产.

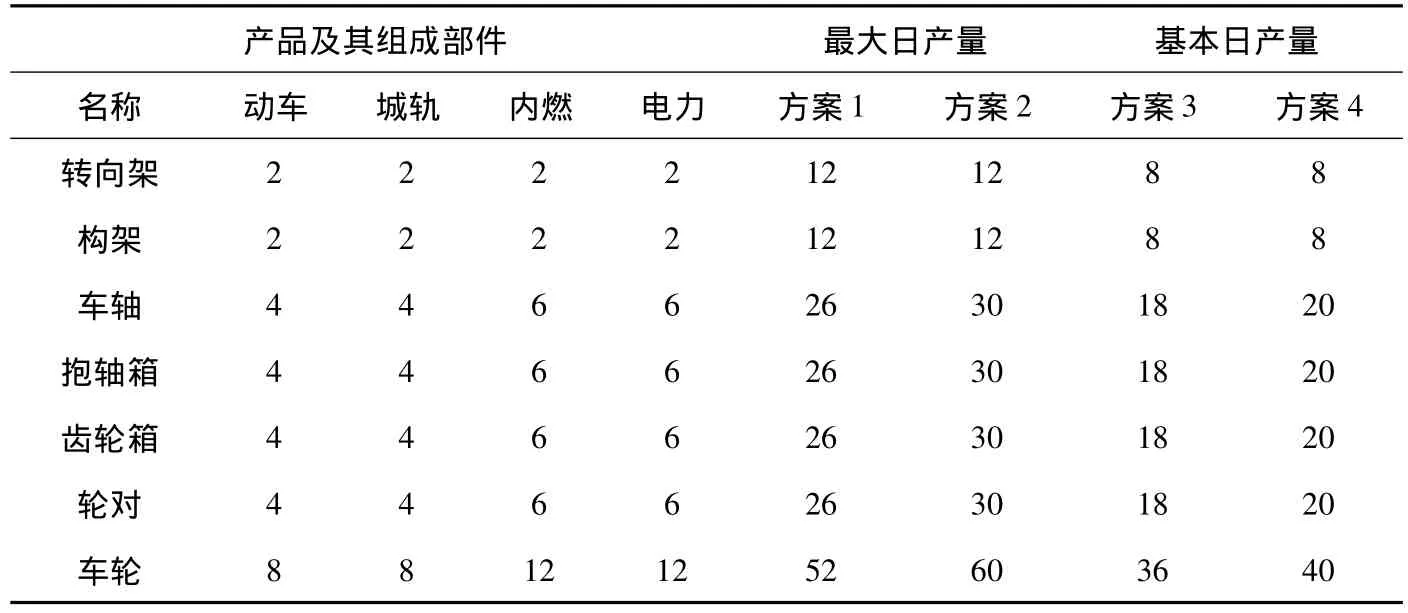
表1 在生产计划下产品主要部件的需求量个

3.2 转向架生产工艺流程

车轮和车轴是生产各种型号转向架产品的关键零件，本文以车轴生产线为例进行分析.

车轴的生产流程如图2所示.

根据该机车厂的转向架生产的工序流程表，车轴生产线中深孔加工工序的加工时间为180min，由1台车轴深孔钻床加工.其余工序的加工时间如图2所示，各工序的加工设备表略.

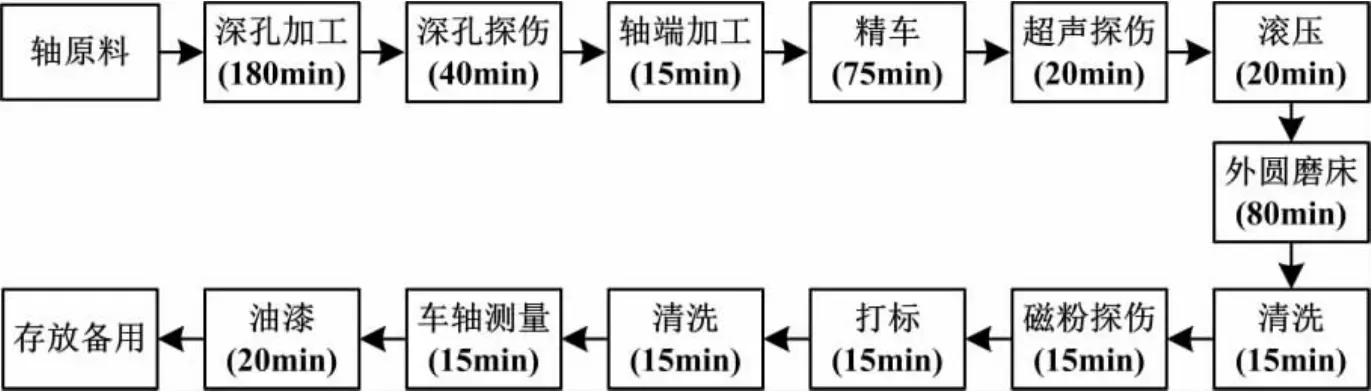
图2 车轴的生产流程图

3.3 转向架工期计算

机车厂班制安排分为三种:工时以7.5 h为一个班次;工时大于7.5 h小于15 h，按两班制进行排班;工时大于15 h小于24 h，按三班制进行排班.

如表1所示，在基本日产量下需要20个车轴.车轴加工采用平行移动的方法，需要经过探伤、滚压、轴端加工，外圆磨床等14个步骤.将生产线分为两个阶段，所有零件采用平行移动方式.第一阶段从探伤工序开始，滚压工序结束，所需加工时间620 min.第二阶段从外圆磨床开始，存放工序结束，所需加工时间655 min.合计完成20个车轴加工周期为2天.其它部件生产线的加工周期计算方法相同.

对于基本日产量生产计划，即方案4的情况，每日完成2台城轨机车转向架，1台电力机车转向架，1台内燃机车转向架的生产，应以生产2台城轨机车转向架工期为准，分为9段工序流程，生产周期为9天，相应的工期甘特图如图3所示.按最大日产量的方案1、2，其加工周期均为11天.

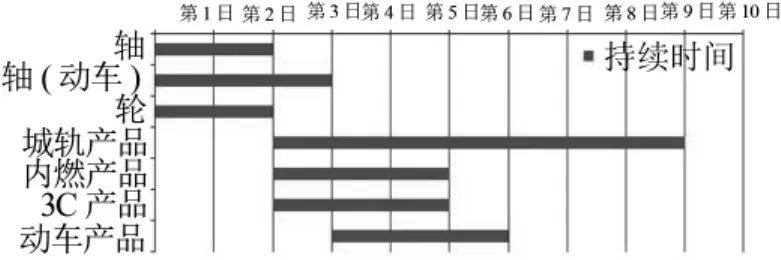
图3 转向架产品生产工期的甘特图

4 基于Anylogic软件的仿真分析

4.1 基于Anylogic软件仿真建模

当系统能够很自然地被描述为一个操作序列时，应该使用离散事件建模.运用Anylogic仿真软件对转向架车间布局规划进行离散事件仿真建模，实现仿真过程.

转向架生产流程的仿真模型如图4所示.

运用Anylogic软件基于离散事件建模.以车轴加工为例，调用source模块，实现原材料车轴在仿真模型里的生成.调用queue模块，实现物料排队依次等待加工的逻辑.调用delay模块，模拟第一道工序磁粉探伤，延迟时间定义为40 min.调用Seize模块，表示资源的调用.调用conveyor模块，表示物料的传送过程.在conveyor模块之后，插入release模块，表示移动结束后即释放该资源.在轴端加工工序完成后，调用seize模块，利用桁架机械手资源.调用conveyor模块，将物料运送至下一工位.调用release模块，释放之前资源.调用sink模块，该段逻辑流程结束.仿真建模逻辑流程图以磁粉探伤至轴端加工逻辑流程图为例，如图5所示.

图4 生产流程的仿真模型图

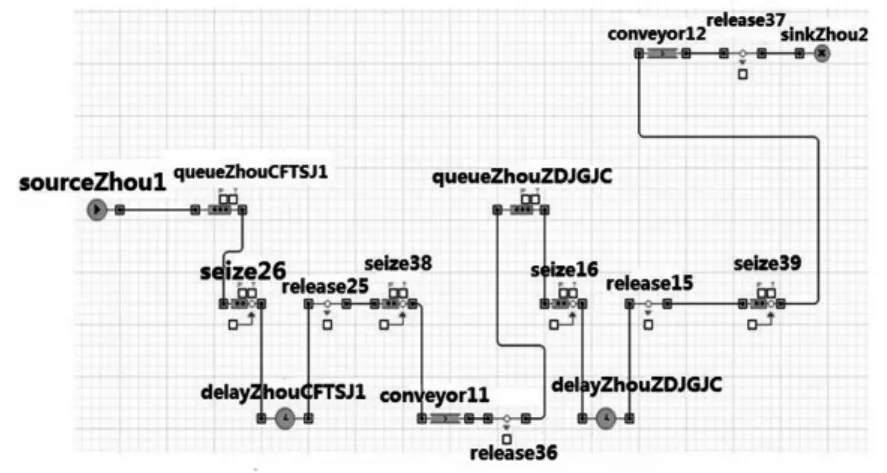
图5 磁粉探伤至轴端加工逻辑流程图

4.2 生产流程仿真及评价指标计算

4.2.1 日产量仿真评价

根据机车厂的最大日生产计划方案4，车轴的最大日产量为30，车轮的日产量为60.其余生产计划经过Anylogic软件仿真分析，仿真结果和理论计算完全一致，均能完成生产计划.车轴及车轮的最大日产量仿真结果如图6所示.

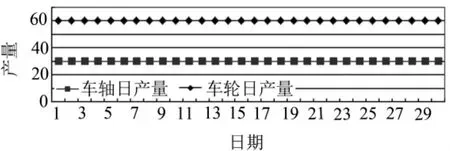
图6 生产计划方案4的车轴及车轮日产量仿真

4.2.2 设备忙闲率

在转向架生产过程中，设备平均忙闲率介于［0，0.5)之间为空闲状态，用A表示.设备平均忙闲率介于［0.5，0.8)之间为正常工作状态，用B表示.设备平均忙闲率介于［0.8，1］之间为繁忙状态，用C表示.设备忙闲率不能超过100%.机车厂部分设备的仿真忙闲率如表2所示.

由表2可知，在最大日产量条件下，龙门加工中心、车轮打标清洗机、加工车轮钻床和AGV等设备均处于繁忙工作状态，这些设备是整条生产线的瓶颈设备，可以考虑增加相应设备数量.

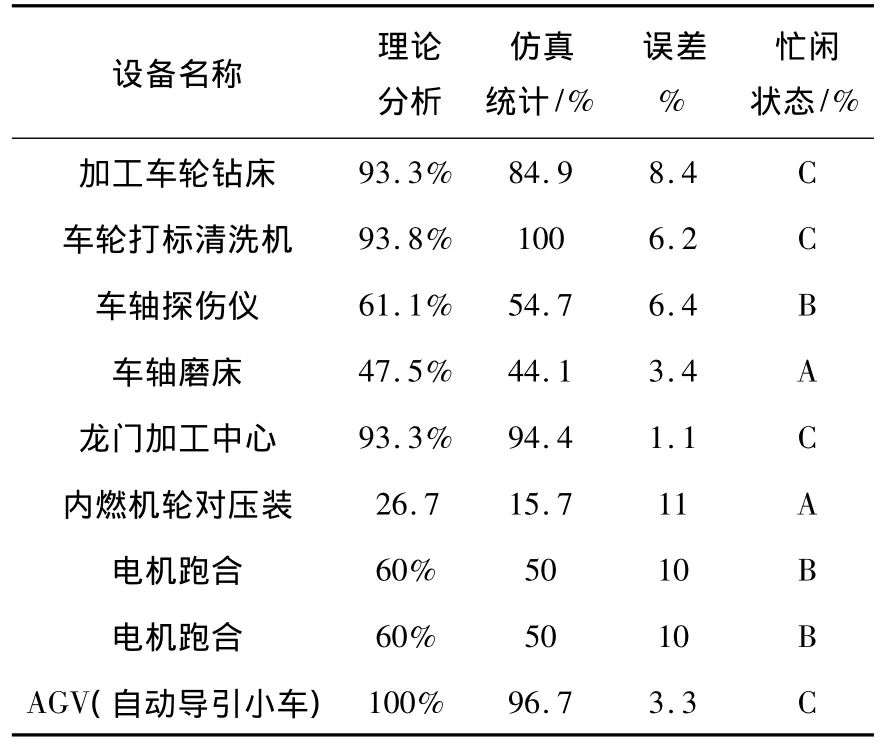
表2 部分设备仿真忙闲率

4.2.3 在制品存放区比例

存放比例方面，基本日产量条件下，车轴加工存放区可以满足存放要求，车轮至静平衡前的存放区不能满足存放需求.在最大日产量条件下，车轮至精车B前存放区、车轮至龙门前存放区、车轮至静平衡前存放区、构架至翻转前存放区、轮对至跑合前存放区、电机跑合后存放区不能满足存放需求.基本日产量条件下存放区的存放状态如表3所示.

表3 基本日产量下的存储状态

4.3 仿真评价及建议

根据机车厂的最大日生产计划，车轴、车轮、转向架等产品的生产计划经Anylogic软件仿真分析，其仿真结果和理论计算完全一致，均能完成生产计划.

部分工序及设备处于繁忙状态，如龙门加工中心、车轮打标清洗机、加工车轮钻床和AGV设备等，可以考虑增加设备数量以应对产量增加.

结合时间最优和距离最优原则，就近调用资源，可以使得资源利用更合理充分.优化原有仿真模型中的AGV转运车的资源调用情况，在仿真模型车轮加工生产线中，结合位置布局和生产加工时间，分工序分别设置资源池，分别配置AGV，就近调用.经过仿真分析，模型中车轮加工生产线共设置7台AGV，AGV设备不会一直处于繁忙状态，也不会限制其它设备生产.

通过对存放区的分析，在基本日产量下应该增大车轮至静平衡前的存放区容积，最大日产量下应该增大车轮至精车B前存放区、车轮至龙门前存放区、车轮至静平衡前存放区、构架至翻转前存放区、轮对至跑合前存放区、电机跑合后存放区的面积.