热管技术及性能分析程序研究

陈其昌

(上海核工程研究设计院有限公司，上海 200233)

热管是一种高效的传热元件，可在较远的距离上实现静态热量传输。20世纪40年代，美国的Gaugler最早提出了热管概念[1]，只是当时并未得到实际应用。20世纪60年代，美国洛斯阿拉莫斯国家实验室(LANL)重新设计出了类似的传热元件[2]，并进行了性能测试试验，并正式命名该传热元件为热管。LANL对热管的研究主要是用于空间技术方面。1965年Cotter首次提出了较为完整的热管理论[3]，为以后的热管理论和应用研究[4]奠定了基础。

随着热管技术的发展和成熟，其在核能领域的应用也越来越受到重视。LANL在20世纪80年代设计了100 kWe的热管式空间反应堆系统SPAR[5]，并进行了相关热管的实验研究。近年来，热管式反应堆由于其无需外力驱动而实现热量非能动传输的特点，被认为在安全可靠性方面具备独特优势，国际上提出一些基于热管反应堆的地面微小型反应堆概念。如LANL和西屋公司分别提出了MW级的热管式微小型反应堆MegaPower[6]和eVinci[7]，可实现车载运输并为偏远基地提供高可靠的能源保障。与此同时，国内相关单位也广泛开展了空间、海洋、地面应用的热管反应堆设计和热管技术的研究[8-17]，其中文献[17]对于热管的相关理论及设计、制造和应用技术进行了较为全面的介绍。

对于热管技术及其工程应用，其传热性能需重点考虑和研究。而热管的传热性能与其自身结构设计及实际工作状态密切相关，其传热性能的计算分析涉及一系列相关理论。本文基于对热管技术及相关理论的研究，开展热管传热性能分析程序的开发和验证，旨为各类新型热管反应堆的设计提供支持。

1 热管及原理

热管工作原理如图1所示。典型的热管结构主要包括管壳、吸液芯及可在管内流动的工质。热管传热的基本原理是通过管内工质在热端(蒸发段)和冷端(冷凝段)的相变传热，以及气、液两相工质分别在汽腔和吸液芯内的反向流动实现的。

热管由于是通过内部工质的相变来实现传热的，与其他传统的传热方式相比具有一些典型的特征。首先热管传热是一种非能动的传热形式，其内部工质的循环并不需要泵或其他外部动力驱动，因此从外部来看它是一种静止的固态导热，这一特点对于核能应用领域具有重要意义，非能动及静态传热大幅提高了反应堆的安全性和可靠性；另一方面，相对于传统固体导热方式，热管又具有高几个量级的导热能力，其内部轴向热阻很小；另外由于热管内是通过气液相变传热的，热管内蒸汽的轴向压降和温差很小。

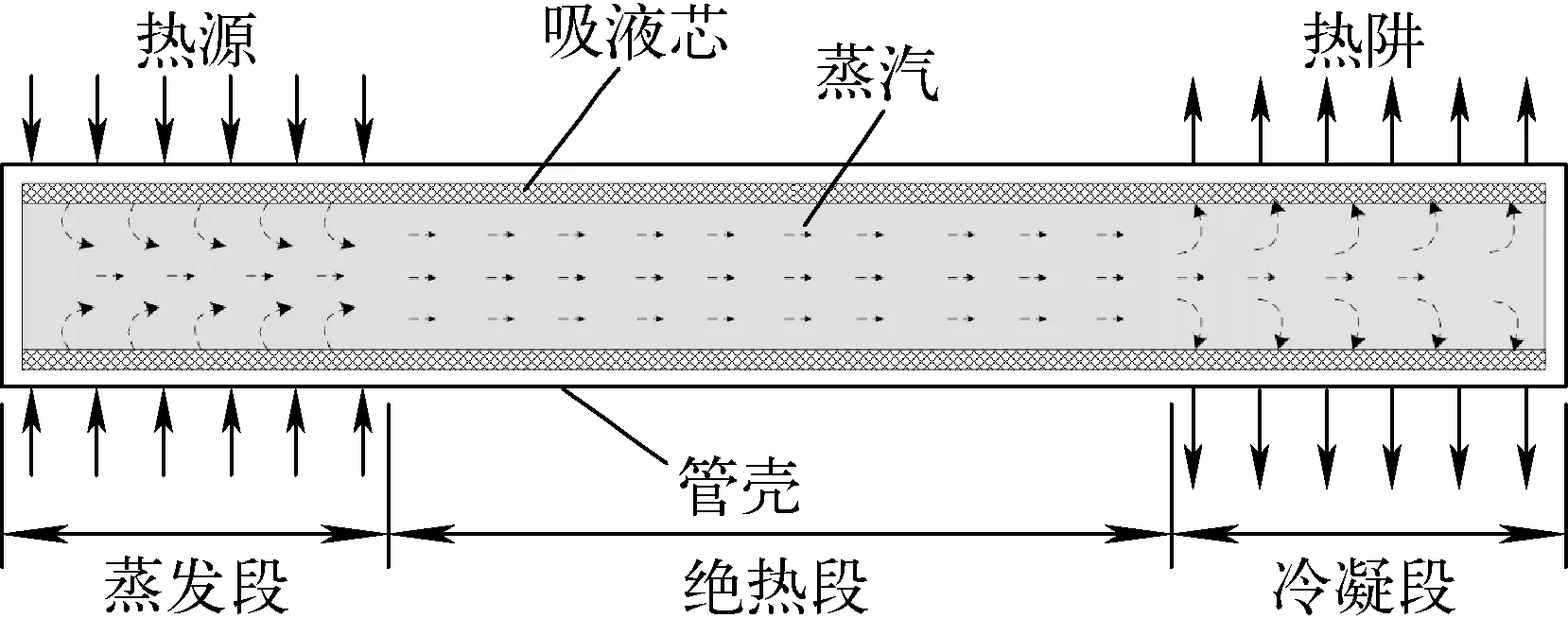
图1 热管工作原理

虽然热管是一种具有良好传热特性的热传输手段，但相比于传统的回路式热传输系统，其传热能力的定量化预测和分析却相对困难，原因在于热管内的传热过程受到了毛细力、蒸发、冷凝、气液流动等多种物理现象的共同作用，这些环节均会影响热管传热能力。为能准确预测热管的传热性能，需建立一套完整的热管传热的理论模型，考虑各种物理现象对传热的影响机理。

2 热管计算理论

2.1 毛细力与流动压降

1) 毛细压差

热管能实现传热的关键一点在于吸液芯结构对于液体工质的吸附和回流，其机理就是多孔吸液芯的毛细力作用，而其基本原理在于液体的表面张力。当热管处于工作状态时，其内部蒸汽的压力与吸液芯内液体压力不同，其压差主要是由气液交界面处月形液面的表面张力提供的。对于特定毛细半径的吸液芯，其能提供的气液压差为：

pv-pl=2σcosθ/rc

(1)

其中：pv和pl分别为蒸汽和液体的压力，Pa；σ为液体工质的表面张力，N/m；θ为液体浸润吸液芯时形成的接触角；rc为吸液芯的毛细半径，m。据此可知，当接触角等于0°(cosθ=1)时，吸液芯能提供最大的毛细压差2σ/rc。因此蒸汽工质从蒸发段流到冷凝段，凝结成液体后再从吸液芯内流回到蒸发段的整个过程中，流动压降不能大于这一最大毛细压差，否则吸液芯的毛细力作用将无法供应足够的工质。这也就意味着热管会存在一个传热极限，即毛细极限。由于存在上述最大毛细压差，因此需分别研究热管内蒸汽和液体工质的流动压降，以判断热管是否达到毛细极限。

2) 液体压降

热管工作时液体流动的轴向压降与吸液芯的结构及热管传热量相关。根据热管内动量、质量和能量平衡关系，热管任意轴向位置x处的压降方程为：

(2)

其中：μl为流体黏度，Pa·s；ρl为流体密度，kg/m3；hfg为汽化潜热，J/kg；AW为吸液芯总横截面积，m2；K为吸液芯渗透率，m2；Q(x)为轴向传热量，W；Fl为液体总摩擦系数，Pa/(W·m)。本文最为关键的参数是K，一般来说，对于层流情况其与流速无关，对于特定的几何可理论计算，而对于其他情况则需要实验获得。当热源在蒸发段为均匀分布时，上式对蒸发段、绝热段、冷凝段分别积分后可得总的液体流动压降：

(Δp)l=(Δp)E+(Δp)A+(Δp)C=

(3)

其中：LE、LA、LC分别为蒸发段、绝热段、冷凝段的热管长度，m；Qtot为轴向总传热量，W。

3) 蒸汽压降

相对于液体流动压降，热管内蒸汽流动压降计算更加复杂，因气体流动可能是层流也可能是湍流，因此惯性效应可能是重要的，同时对很多情况来说可压缩性也是要考虑的重要因素。对于层流情况，蒸汽压降公式与液体压降公式类似，仅是蒸汽摩擦系数Fv的定义略有不同，即：

(4)

其中：μv为蒸汽黏度，Pa·s；ρv为蒸汽密度，kg/m3；Av为蒸汽流道横截面积，m2。

对于层流情况，摩擦系数与雷诺数Re无关，但如要考虑湍流(Re>2 300)情况，那么摩擦系数则需根据具体雷诺数进行修正，其表达式为：

(5)

而当蒸汽马赫数Ma大于0.2时，还需进一步考虑蒸汽的可压缩性，根据马赫数进行摩擦系数的修正。

(6)

其中，γ为气体的绝热系数。

当惯性效应不明显时，对上面的蒸汽压降公式(式(4))积分后即可得到类似于式(3)的蒸汽压降表达式。而当惯性效应很重要时，流动分析较复杂，此时没有完全满足要求的解析表达式。Cotter[3]给出了在蒸发段均匀质量注入、在冷凝段均匀质量输出的层流不可压缩流动的结果。对于蒸发段，其惯性力压降为：

(7)

而在冷凝段，由于蒸汽速度降低，蒸汽压力会出现恢复升高，但仅能部分恢复，有：

(8)

2.2 传热极限

热管虽具有较好的传热性能，但其传热量与其结构尺寸、工作介质、工作温度等密切相关，热管的传热存在一系列的传热极限。其中主要的传热极限包括毛细极限、黏性极限、声速极限、携带极限、沸腾极限等。本文传热极限相关计算模型主要来自文献[4]。

1) 毛细极限

热管内由于吸液芯的毛细力存在一个极限，能提供的气液压差有一最大值。因此要求热管内沿工质流动方向蒸汽的压差和液体的压差之和要小于最大毛细压差。根据上述毛细压差、液体压差及蒸汽压差计算公式，得出最大的毛细传热极限为：

(9)

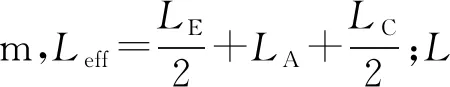
K是毛细极限计算中的1个重要参数，它是吸液芯液体流道几何形状的函数，一般可通过实验测定，但对于特定规则几何的吸液芯则可用理论公式计算。不同吸液芯结构的渗透率计算方法列于表1[4]。其中对于环道式、干道式及覆盖沟槽式吸液芯，本文仅给出环道、干道、沟槽流道的渗透率，而它们实际上是复合吸液芯，其液体流道包括了丝网吸液芯内部流道以及环道、干道、沟槽流道，因此最终渗透率应是这两部分的截面积权重平均。对于环道式和矩形沟槽式吸液芯，其渗透率计算还需相应的流动摩擦系数(fRe)实验数据，图2示出了文献[4]的相关结果。

表1 不同吸液芯结构的渗透率

图2 环道和矩形沟槽内摩擦系数

2) 声速极限

对于可压缩气体流动，热管还存在声速极限。热管内的蒸汽由于惯性力作用，其流速可能达到声速而出现阻塞现象，此时最大的传热量被称为声速极限。对于蒸发段，假设为一维可压缩气体流动，轴向传热将与局部马赫数相关，其声速极限[4]为：

(10)

其中：QS为最大声速传热极限，W；Rv为蒸汽气体常数，Rv=R/M，R为气体常数，J/(mol·K)，M为原子量；ρo和To分别为蒸发段起始点的蒸汽密度(kg/m3)和温度(K)。

3) 黏性极限

由于黏性力的作用，蒸汽的压力在热管冷凝段末端降至0时，受到的传热限制称为黏性极限。对于相对较长的热管，其黏性效应将占主导地位，可能发生黏性极限。其传热极限计算如下[4]：

(11)

其中：d为蒸汽流道直径，m；po为蒸发段起始点的压力，Pa。

4) 携带极限

当热管中的蒸汽流速足够高时，气液交界面存在的剪切力可能将吸液芯中的液体携带入蒸汽流，从而限制传热能力，称为携带极限。如果作用在逆流蒸汽和液体之间的剪切力足以“撕裂”液膜表面张力而夹带液滴，那么就会出现携带极限。根据吸液芯表面孔隙的等效水力半径，携带极限传热公式[4]为：

(12)

其中，re为吸液芯孔隙的等效水力半径，m。

5) 沸腾极限

如果热管蒸发段管壁温度太高，吸液芯中的工质出现沸腾则会阻碍工质的循环流动，此时将会出现沸腾极限。根据蒸发段吸液芯材料中蒸汽气泡的形成和生长(稳定性)分析，可得出的沸腾极限如下[4]：

(13)

其中：Le为蒸发段长度，m；ke为吸液芯等效热导率，W/(m·K)；Tv为局部饱和温度，K；ri和rv分别为吸液芯的内径和外径，m；Δpl和Δpv分别为液体和蒸汽的流动压降，Pa；rn为气泡生成所需临界半径，m，根据相关研究可保守地取值为2.54×10-7m。

热管传热过程中，在蒸发段和冷凝段均需通过管壁及吸液芯结构与热源及热阱的热量交换。而热管的沸腾极限则与吸液芯的等效热导率直接相关，下面分别讨论不同吸液芯结构等效热导率的计算。吸液芯的等效热导率主要与吸液芯材料以及其中工质液体的热导率相关。同时对于环道式、覆盖沟槽式结构，其等效热导率实际是环形流道或沟槽与上部丝网吸液芯的串联结构，因此可通过各自热导率组合计算得到。不同吸液芯的等效热导率的具体计算方法列于表2。

表2 不同吸液芯结构的等效热导率

3 HEPAC程序开发

3.1 程序简介

根据上述相关理论模型，开发了热管传热性能分析程序HEPAC，可针对不同吸液芯结构的热管进行温度、压力、传热量及传热极限的计算。HEPAC设计为一个通用的热管程序，尽管目前程序仅包含了钠的物性参数计算，但所有热物性参数均通过独立的子程序来提供，因此可方便地扩展到其他工质类型。类似地，目前程序包含了沟槽式、丝网式、干道式等5种吸液芯结构的热管，而吸液芯结构特征参数也是通过单独、可扩展的子程序计算，后续可进一步扩充其他类型的吸液芯结构。

根据实际计算需求，HEPAC程序设计了多种功能模式。基本功能模式是针对一系列不同的热源和热阱温度进行热管传热量的计算，从而得到热管对于不同运行条件的静态响应。一旦热管达到其中的某个传热极限，将会在输出中给出适当的提示。另外，程序具备其他4种功能模式，即通过改变4种边界条件(热源和热阱温度及传热系数)中的1个，来搜索最低的传热极限。HEPAC程序目前已进行了初步的测试和验证，鉴于相关实验数据较少，目前主要针对声速极限和毛细极限开展，相关计算结果与测量数据吻合良好。

图3示出了HEPAC程序的主要计算流程。HEPAC程序的主要目的是计算各种类型热管的传热极限，本文前面理论模型部分已给出各种传热极限的计算方法。然而热管的传热极限与其具体的运行状态密切相关，热管的温度、压力、传热量等均会影响其传热极限，因此HEPAC程序首先会根据热管运行的初始边界条件(热源、热阱)进行压力、温度、传热量等计算，然后计算相应工作状态下热管的传热极限，并根据传热极限重新搜索热管的工作状态直至其传热量与传热极限一致。HEPAC程序可实现一系列不同工况下热管传热极限的计算，从而给出热管在不同工作温度下的传热极限变化曲线。

图3 HEPAC程序流程图

3.2 程序模型

HEPAC程序采用热阻计算模型进行热管内各传热过程的计算。热管的热阻计算涉及蒸发段、冷凝段的各传热过程，目前热阻计算模型假设在蒸发段和冷凝段是等温的，同时不考虑通过热管管壁和吸液芯的轴向热传导。认为热管蒸发段处于温度为TB(管外流体温度)的热源环境中，而冷凝段处于温度为TS的热阱环境中。对于从热源到热阱的热量传输过程，其热阻和温差主要考虑以下8个传热环节：1) 热源到热管外表面的表面换热；2) 蒸发段管壁的导热；3) 蒸发段浸透吸液芯材料的有效导热；4) 蒸发段吸液芯材料到蒸汽的沸腾传热；5) 蒸汽到冷凝段吸液芯材料的冷凝传热；6) 冷凝段浸透吸液芯材料的有效导热；7) 冷凝段管壁的导热；8) 热管外表面到热阱的表面换热。

严格来说，热管内的热阻还需考虑不同热管段蒸汽的传输过程，由于其热阻一般较小，因此本文忽略不计。热源到蒸发段管壁的传热可通过对流换热系数计算得到：

Q=hAΔT=hBπDLe(TB-Teo)

(14)

其中：hB为对流换热系数；D为热管外径；Teo为蒸发段外壁面温度。类似地，在冷凝段的换热也可通过冷凝段对流换热系数进行计算。

通过热管壁面的径向导热由下式计算：

(15)

其中：ke为蒸发段管壁热导率；Tei为蒸发段内壁面温度；ro和ri分别为热管外径和内径，对于冷凝段其计算过程类似。另外对于蒸发段和冷凝段吸液芯的径向导热计算也是采用类似的公式。

沸腾和冷凝表面的热阻计算基于饱和蒸汽的克拉伯龙关系式，其传热率为：

(16)

其中：ps为温度T对应的饱和压力；AE为总的蒸发面积；Te-Tv为沸腾交界面上的温差。这一表达式可用来定义一个等效的沸腾热阻，对于冷凝过程其表达式类似。

根据上述各热阻计算模型，可得到整个热管的总热阻，根据边界条件的热源和热阱温度，即可计算新的热管传热量，并由此进一步得到热管各环节的温差。而有了热管内部各处的温度分布，即可计算各种传热极限。

3.3 程序验证

1) 案例1

文献[18]给出了一种干道式钠热管的相关实验结果，其进行实验的热管结构如图4所示。该热管外壁直径为2.5 cm，蒸发段长度为0.3 m，绝热段长度为0.1 m，冷凝段长度为0.7 m。热管内部有1层丝网式的吸液芯，其毛细半径为0.085 mm。同时内部设置了5个供液体流动的干道芯，干道内直径为2.3 mm。干道式热管的优点是具有大的毛细压差(取决于丝网芯)的同时，又具有较小的液体流动阻力。HEPAC程序计算采用多个工况的固定热源温度边界条件，在每个热源温度工况下通过搜索热阱温度获得相应的热管温度和传热极限。

图4 干道式热管结构

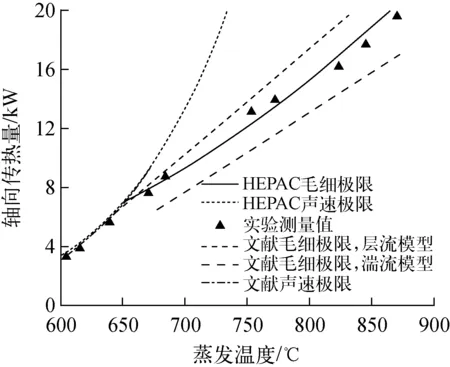
图5 案例1结果对比

图5示出了HEPAC程序计算结果与文献[18]相关结果的比较，本文分别针对声速极限和毛细极限进行了比较。分析表明，在较低温度工况下，该热管受到的是声速传热极限限制，而约在蒸发温度650 ℃开始受到毛细极限限制。从图5可看出，HEPAC程序相关计算结果与实验值吻合较好，其声速极限曲线与文献中预测曲线也很好地吻合，而毛细极限结果相比文献中层流和湍流计算模型，HEPAC程序结果与实验值吻合更好。

2) 案例2

文献[19]对不同工质的热管进行了声速极限的研究，鉴于目前HEPAC程序中仅有钠的相关物性数据，因此本文仅对其中钠热管的声速极限进行对比。该案例中钠热管为环道式吸液芯结构，其结构如图6所示。其中在丝网吸液芯和管壁之间，留有一定厚度的环腔通道，便于液体工质在其内部的流动。该热管外径为13.8 mm，壁厚为0.9 mm，细丝网吸液芯和液体环腔的厚度均为0.15 mm。根据实验测量，其丝网吸液芯的毛细半径为9.5 μm。实验中，该热管总长度为137 cm，其中蒸发段长度为14 cm，冷凝段长度为110 cm。HEPAC程序计算边界条件设置与案例1相同。

图6 环道式热管结构

图7 案例2结果对比

图7示出HEPAC程序计算的声速极限与文献[19]结果的比较，本文仅对钠热管的结果进行对比，可看到HEPAC程序结果与文献的计算和实验结果吻合较好。

3) 案例3

文献[20]对于空间堆应用热管进行了相关计算和实验研究，其中给出了一种钠热管的传热性能实验数据。该热管同样为环道式吸液芯结构，热管外径为15.9 mm，环腔厚度为0.66 mm，丝网吸液芯的毛细半径为23.5 μm。热管蒸发段、绝热段和冷凝段的长度分别为30、100和33 cm。HEPAC程序计算边界条件设置与案例1相同。

图8示出了HEPAC程序计算的声速极限与毛细极限的结果。可看到，文献[20]中其分别采用层流模型和湍流模型计算的声速极限和毛细极限差别较大，而HEPAC程序计算结果与实验结果吻合较好。

图8 案例3结果对比

4 结论与展望

根据热管传热机理及相关理论研究基础，开发了热管传热性能分析程序HEPAC，目前具备了不同吸液芯结构的钠热管的温度、压力、传热极限等计算能力。利用HEPAC程序分别对不同类型的钠热管进行了传热极限的计算和分析，并与实验数据进行了对比。结果表明HEPAC程序计算结果与相关实验数据吻合良好，程序能用于各类热管声速极限和毛细极限的预测分析。

HEPAC程序的开发为各类新型热管式反应堆研究提供了工具支撑。后续还将在程序功能开发及测试验证方面进一步完善。一方面增加锂、钾、钠钾合金等不同工质的物性数据，另一方面开发更多的吸液芯结构形式，以拓展HEPAC程序的适用范围；同时还将进一步开展各类传热极限与实验数据的对比验证，完善相关理论模型，提高程序预测精度和置信度。