MW级空间核反应堆系统热管式辐射散热器分析及优化
2020-07-14张昊春刘秀婷魏前明游尔胜孙铭远
张昊春,刘秀婷,魏前明,游尔胜,孙铭远
(1.哈尔滨工业大学 能源科学与工程学院,黑龙江 哈尔滨 150001;2.中国核动力研究设计院 中核核反应堆热工水力技术重点实验室,四川 成都 610213)
空间核动力系统因其输出功率高、能量密度大、工作时间长[1]成为深空探测最具发展前景的选择之一。由于大功率空间核反应堆系统需要大量散热,故其辐射散热部分体积通常占据整体的60%左右,因此,对大功率空间核反应堆系统的辐射散热器进行设计和分析优化具有实际意义和参考价值。
已有的热管式空间冷却堆热电转换系统皆为概念设计方案,主要是堆芯热管所选用的工质和热电转化方式不同。如采用锂热管冷却堆芯、分段式静态热电偶转换器进行热电转换的HP-STMCs[2]和采用钠热管冷却堆芯、碱金属热电转换装置(AMTEC)进行热电转换的SAIRS[3](scalable AMTEC intergraded reactor space power system)热管式空间冷却堆,以上两种系统均采用钾热管通过散热器将废热排向太空。此外,还有用于火星表面活动的电源、热量通过钠热管被带出堆芯传递到能量转化系统的HOMER[4](heatpipe-operated mars exploration reactor),通过自由活塞式斯特林发电机实现热电转换的kW级空间核反应堆电源Kilopower等[5]。近年来热管式辐射散热器的性能研究是国内外研究热点,谢荣建[6]运用遗传算法对地球静止轨道热控系统中热管辐射散热器进行性能研究,得出了热控制要求下最轻的散热器质量。刘逍等[7]对空间堆热管式辐射散热器进行初步设计分析,得到了相应功率下,必要热管根数及最佳冷却流体流量。Jebrail等[8]对热管式热电偶散热器进行了研究。Bieger[9]对微重力环境下的热管长度、厚度参数进行优化设计,在满足热管散热功率的条件下,得出其设计热管的最佳参数。Sam等[10]提出一种应用于实际工程设计的热管式散热器的优化,考虑到功率最大的状态、太阳能通量、散热和元件的设计温度上限,确定最佳散热器的尺寸。Wenwen等[11]为俄罗斯TOPAZ-Ⅱ空间核电源系统提出了一种碱金属热管式散热器,采用以钾为工质的高温热管,丝网作为芯层,采用不锈钢制成,通过辐射散热,选择整体碳翅片覆盖和连接热管作为整个辐射散热器。本文基于热管式散热器的工作原理,通过遗传算法,获得多因素下散热器质量的最优解,以降低空间核反应堆的运行负荷。
1 工作原理

图1 空间热管式辐射散热系统示意图
热管式空间辐射散热器由多个热管式辐射散热器单元组成,其工作流程为:流动的冷却剂工质从热源吸收经热电转换后的废热,在冷却剂工质流经辐射散热器时,热量被传递至辐射散热器,辐射散热器上安装热管,热量经热管传递给辐射翅片,辐射翅片底部加装隔热层,屏蔽热量向航天器的辐射,热量最后通过辐射排向外太空。图1为空间热管式辐射散热系统示意图。热管管壳材料选取高强度质量比、高导热率的镍合金,工作介质选择熔点为98 ℃、沸点为892 ℃的液态金属钠[12],其工作温度为600~1 200 ℃,热管吸液芯材料选择钼铼合金(Mo-14%Re)[13],热管与裸碳纤维翅片焊接选用导热系数为219 W/(m·K)的活性钎焊合金Ticusil[14],热管冷凝段钎焊连接裸碳纤维翅片[15]。冷却剂回路工作介质选择液态金属钾,其物性参数参见文献[16-17]。热管的工作原理如图2所示。典型的热管由热管外壳、紧贴内壁的吸液芯毛细多孔材料、端盖构成。热管被加热的一端称为蒸发段,热量经热管壁传递给吸液芯(多孔材料),再传递给吸液芯中的液态工作介质使之蒸发气化,该热量即为液态工作介质的蒸发潜热,由于热管蒸发段蒸气温度高所引起的压力差驱动蒸气从中心气腔流向热管另一端,高温蒸气在另一端遇冷凝结,同时释放出潜热,这一端被称为冷凝段。热管冷凝段冷凝的饱和液体由于受到管芯多孔材料的毛细力重新流回蒸发段。如此循环往复,热量便由热管一端传递至另一端。

图2 热管工作原理示意图
2 参数选择和模型建立
2.1 主要设计参数
参考辐射散热器的经典参数,对于MW级空间核电源,堆芯功率为3.2 MW,转换效率为31.8%,废热排出要求为2.18 MW[15]。辐射散热器进口温度为800 K,冷却剂回路质量流量为8 kg/s,冷却剂回路管道直径为50 mm。辐射散热器中热管的尺寸参数列于表1。

表1 辐射散热器热管设计参数
冷却剂回路工作介质可选择液态金属钾(临界温度2 222 K,临界压力16.2 MPa),钾物性参数可由式(1)~(4)计算。
λ=92.95-0.058 1T+11.727 4×10-6T2
(1)
cp=1 436.72-0.580T+4.627×10-4T2
(2)
lnμ=-6.484 6-0.429 03lnT+485.3/T
(3)
ρ×10-3=0.902 813 76-0.169 907 11×
(T×10-3)-0.268 647 69(T×10-3)2-
0.505 681 88(T×10-3)3-0.465 379 12×
(T×10-3)4+0.203 781 07(T×10-3)5-
0.034 771 31(T×10-3)6
(4)
式中:ρ为液体密度,kg/m3;λ为导热系数,W/(m·K);cp为比定压热容,kJ/(kg·K);T为温度,K;μ为动力黏度,Pa·s。
2.2 换热计算
1) 热管式辐射散热器与宇宙空间辐射散热
当MW级空间辐射散热器正常工作时,热量来源为冷却剂温降,热量去向为空间环境的辐射散热,选取第i个热管式辐射散热器单元作为研究对象,热管式辐射散热器单元由单根热管、加装在热管两侧的裸碳纤维翅片组成。由于MW级航天飞行器处于深空宇宙,无对流换热,考虑到热管的等温性,将三维翅片沿热管方向简化成单位长度的二维翅片模型,如图3所示。

图3 二维翅片辐射散热模型
记翅长(相邻热管间距)为Lf、翅厚δf、翅根温度为Tr。以翅根与翅片下端绝热层的交点为坐标原点建立直角坐标系。x在0~Lf之间取值,y在0~δf之间取值,n为节点个数。
二维模型内部节点控制方程[18]如下:
∂2T/∂x2+∂2T/∂y2=0
(5)
上边界:
λT(i,ny)=λT(i,ny-1)-
(6)
式中:ε为发射率;σ为辐射常数,W/(m2·K2)。
运用有限差分和迭代法,可计算二维翅片模型稳态热分布,通过迭代计算可得出单位翅长辐射面各点的温度。求得辐射面各点温度后,可由式(7)计算热管式辐射散热器单元的辐射散热量。
(7)
2) 热管式辐射散热器的单元流体换热计算
热量由冷却剂传递到热管蒸发段外壁的过程中,换热热阻分为两部分:(1) 冷却剂与冷却剂管道的对流换热;(2) 热量由冷却剂管内壁传递到冷却剂管外壁。则该过程总的换热热阻R1[19]为:
(8)
式中:din、dout、lp和tp分别为冷却剂管道内径、外径、长度和厚度,m;λcp为冷却剂管道管壁径向导热系数,W/(m·K);hc为冷却剂管道管内换热系数,W/(m2·K)。
再考虑热量由热管蒸发段外壁传递至裸碳纤维翅片翅根处的换热热阻R2。
R2=Rhpv+Rhpc+R0
(9)
设热量从热管蒸发段管壁外部传到热管蒸发段内表面过程中沿管壁径向的导热热阻为Rhpv,则有:
(10)
式中:dhpvi、dhpvo和thpv分别为热管蒸发段内径、外径和管壁厚度,m;λhp为热管管材径向导热系数,W/(m·K)。
热管吸液芯管芯的结构选择流动阻力小、毛细力大的干线芯管芯,热管沿管径方向的热阻很小,且由于热管沿轴向的等温性,则可忽略热管工质从热管蒸发段到冷凝段的换热热阻。设热量从热管冷凝段管壁内部传到冷凝段外表面过程中沿管壁径向的导热热阻为Rhpc,则有:
(11)
式中,dhpci、dhpco分别为热管冷凝段内径、外径,m。
设热量通过热管冷凝段外壁与翅片连接的钎焊层的导热热阻为R0,则:
(12)
式中:λ0为钎焊层材料径向导热系数,W/(m·K);t0为钎焊层厚度,m。
则冷却剂传递到裸碳纤维翅片翅根总换热热阻R可由下式计算:
R=R1+R2
(13)
3) 热管式辐射散热器系统热分析
已知热管式辐射散热器冷却剂入口温度Tf1,1及总设计散热功率Q0,采用迭代法从第1个热管式辐射散热器单元开始计算,对热管式辐射散热器系统进行热分析。
假设第i个热管式辐射散热器单元冷却剂出口温度为Tf2,1,根据式(14)可计算热管式辐射散热器单元单位时间内从冷却剂吸收的热量Qi,由式(5)可计算裸碳纤维翅片翅根温度Tr,进而由式(7)可求得热管式辐射散热器单元的辐射散热量QR,i。
Qi=cpm(Tf1,i-Tf2,i)
(14)
A=N(2Lf+do)lhpc
(15)
M=2NLflhpcδfρfin+
(16)
式中:ρfin为裸碳纤维翅片密度,kg/m3;ρhp为热管材料密度,kg/m3。
3 分析及优化
3.1 热管式辐射散热器质量影响因素
选取冷却剂质量流量m、裸碳纤维翅片长度Lf、裸碳纤维翅片厚度δf、热管式辐射散热器入口温度Tf1为优化参数对热管式辐射散热器系统质量M进行优化。
1) 翅片厚度δf
选取Lf=5 cm、m=7 kg/s、Tf1=800 K,探讨δf对M的影响,结果示于图4。使用钾作为冷却剂,当δf由0.1 mm增加到0.9 mm时,M先减小后增大,当δf为0.2 mm时,M取得最小值972.9 kg。这是因为当δf过小时,由热管传递至裸碳纤维翅片的热量也很小,导致裸碳纤维翅片表面温度过低,热管式辐射散热器单元辐射散热量小,所需辐射单元数较多,故热管式辐射散热器系统总质量增加。

图4 σf对M的影响
2) 翅片长度Lf
选取δf=0.2 mm、m=7 kg/s、Tf1=800 K,探讨Lf对M的影响,结果示于图5。从图5可看出,当Lf从1.5 cm到9.5 cm变化时,热管式辐射散热器质量呈现先减小后增大的趋势,当Lf为5 cm时热管式辐射散热器质量取得最小值972.9 kg。这是由于Lf增加到一定程度时,裸碳纤维翅片热阻很大,外侧表面温度很低,导致其辐射能力变差。

图5 Lf对M的影响
3) 冷却剂质量流量m
选取δf=0.2 mm、Lf=5 cm、Tf1=800 K,探讨m对M的影响,结果示于图6。当冷却剂质量流量m增大时,热量经由冷却剂至裸碳纤维翅根的R越小,则Tr越大,进而裸碳纤维翅片辐射热量越大,热管式辐射散热器系统质量越小。当质量流量大于9 kg/s时,热管式辐射散热器系统质量基本不变,考虑到泵功率不应超出核电源电功率的5%,且当质量流量大于9 kg/s时,热管式辐射散热器系统质量基本不变,则流量m取9 kg/s为宜。

图6 m对M的影响
4) 入口温度Tf1
选取δf=0.2 mm、Lf=5 cm、m=7 kg/s,探讨Tf1对M的影响,所得变化关系曲线如图7所示。当热管式辐射散热器入口温度Tf1增大时,Tr越大,裸碳纤维翅片辐射热量越大,热管式辐射散热器系统质量M越小。但依靠增加热管式辐射散热器入口温度Tf1来降低热管式辐射散热器系统质量制约因素很多,故结合前人设计经验热管式辐射散热器入口温度Tf1选择800 K为宜。
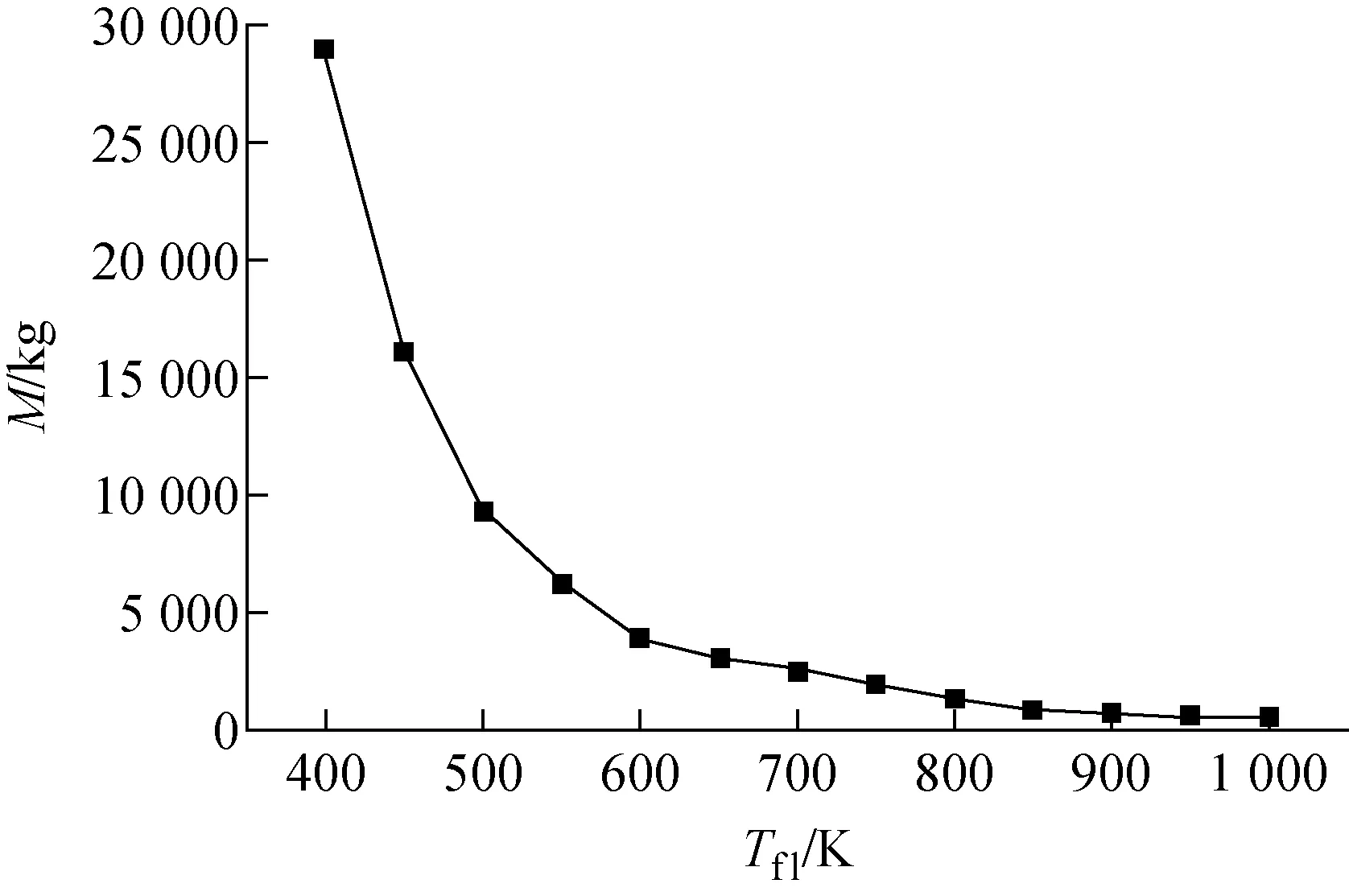
图7 Tf1对M的影响
3.2 遗传算法对辐射散热器质量的优化
1)Lf变化时辐射散热器优化结果
在其他参数不变的情况下,选取裸碳纤维翅片长度Lf为4.5~5.5 cm,利用遗传算法,设置初始种群数n为40、交叉率Pc为0.7、变异概率Pm为0.001 5、最大代数为150、代沟G为0.9,得到的最终优化结果如图8所示。图8表明,当Lf取5 cm时,M取得最小值912.10 kg。遗传算法结果表明,当Lf取5.07 cm时,M取得最小值912.066 kg,此结果表明Lf在5 cm附近时M取得最小值。
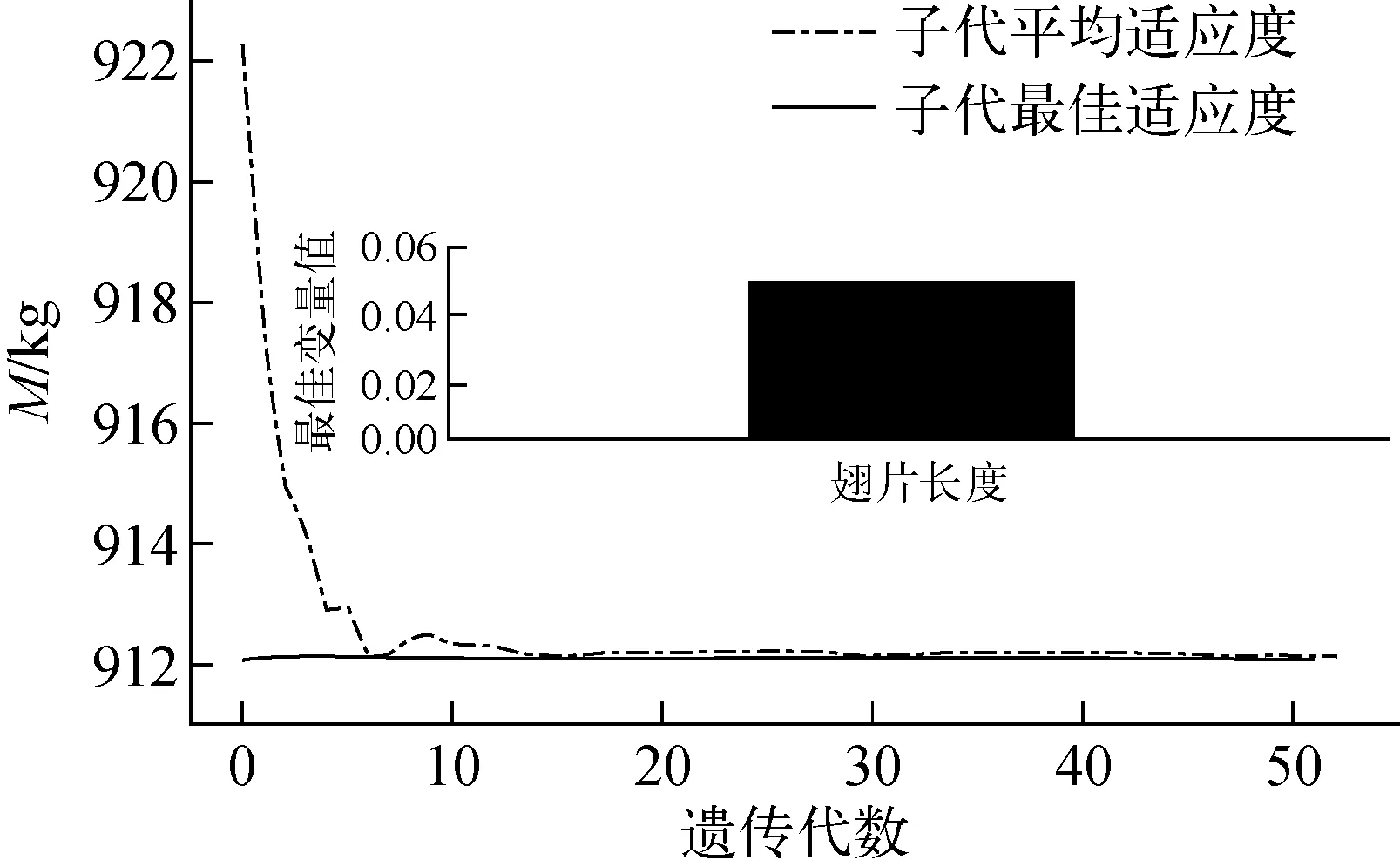
图8 裸碳纤维翅片长度遗传算法优化结果
2)δf变化时辐射散热器优化结果
在其他参数不变的情况下,选取δf为0.1~0.2 mm,利用遗传算法,设置遗传算法参数如前文所述,得到优化结果如图9所示。
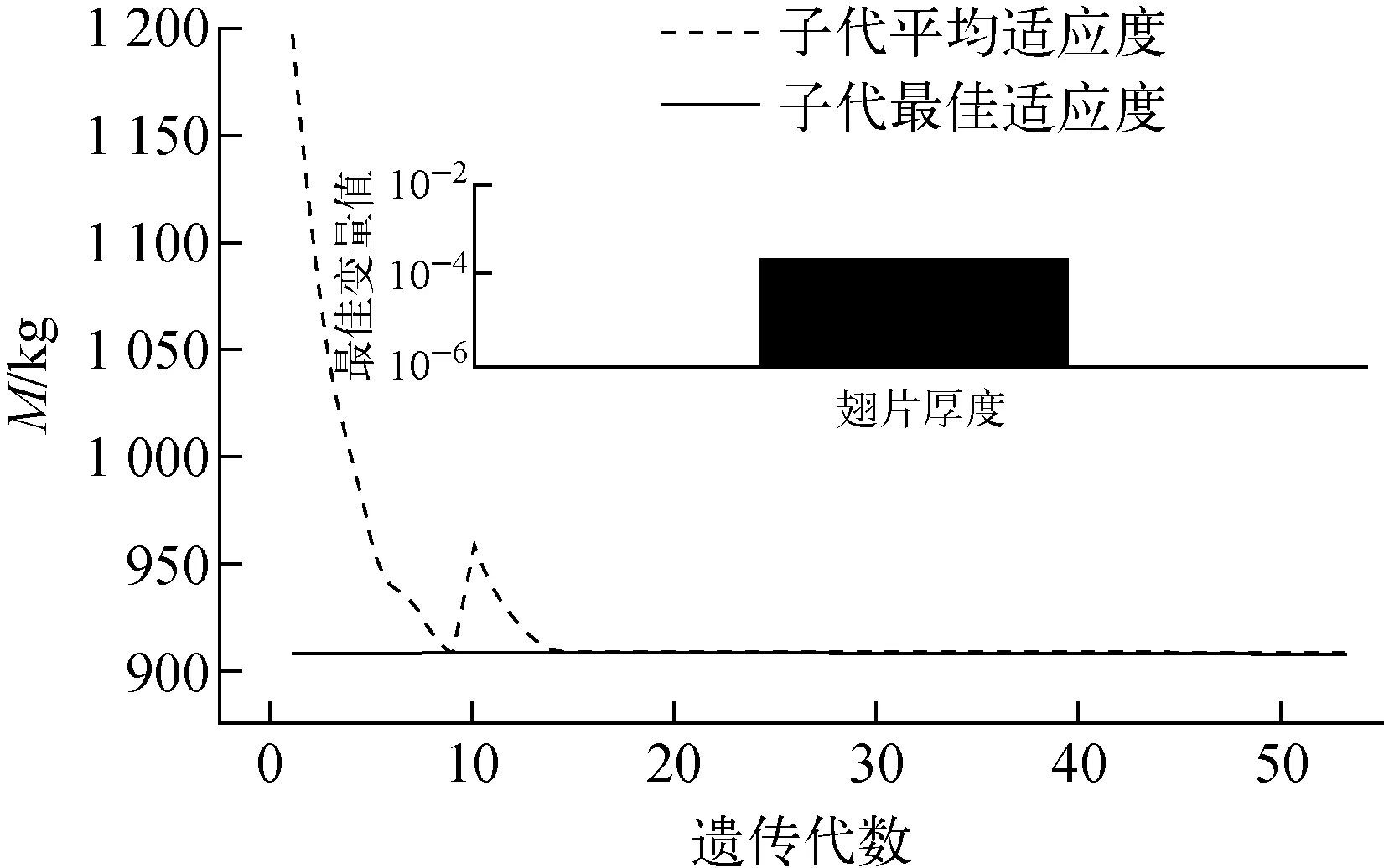
图9 裸碳纤维翅片厚度遗传算法优化结果
图9表明,当δf取0.16 mm时M取得最小值907.816 kg。为更好地探讨辐射散热器的质量优化和对比分析,采取多参数优化所得结果。
3) 多参数辐射散热器质量优化
选取Lf为4.5~5.5 cm、δf为0.1~0.2 mm、m为6~9 kg/s、Tf1为400~800 K。设置遗传算法运行参数,其中初始种群数n为40、编码串长l为37、交叉率Pc为0.7、变异概率Pm为0.001 5、最大代数为150、代沟G为0.9。变量与目标函数M的遗传算法如图10所示。
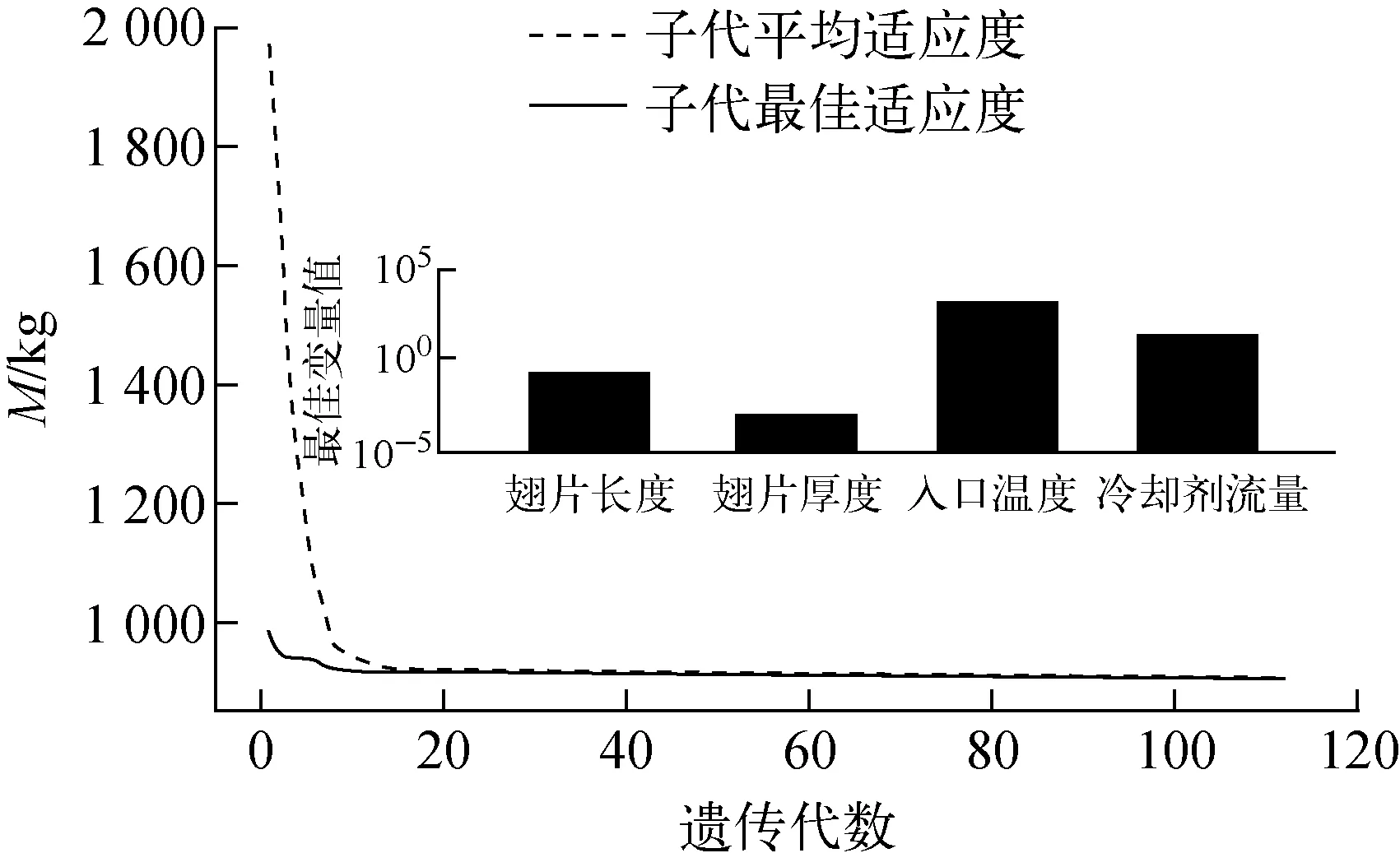
图10 多变量遗传算法优化结果
比较遗传算法和穷举法的结果可知:对于穷举法,当Lf取5 cm、σf取0.2 mm时,M取得最小值912.10 kg;对于遗传算法,当Lf取5.07 cm、δf取0.16 mm、Tf1取800 K、m取9 kg/s时,M取得最小值906.593 kg,优化了0.63%的系统质量。
4 结论
本文对MW级空间核反应堆系统的热管式辐射散热器进行了设计,并以辐射散热器质量为优化目标,在遗传算法的基础上研究了冷却剂质量流量m、裸碳纤维翅片长度Lf和厚度δf及辐射散热器入口温度Tf1对散热器质量M的影响,得到以下结论:
1) 建立了热管式辐射散热器热阻分析数学模型,计算得到了不同工况下辐射散热器的系统质量,并给出了最优解;
2) 散热器质量M随质量流量m、入口温度Tf1的增加而减小,取m为9 kg/s时可获得较好优化结果;
3)M随Lf和δf的增大呈先减小后增大的趋势,Lf为5 cm和δf为0.2 mm时取得最小值972.9 kg;
4) 当Tf1=800 K、Lf=5 cm、δf=0.16 mm、m=9 kg/s时,M最小,此时M为906.593 kg,优化了0.63%的系统质量。
