EOF重构声速剖面对深水多波束的声速改正分析

2020-04-25张孝首周兴华唐秋华王盼龙丁继胜王永康

海岸工程 2020年1期

张孝首周兴华*唐秋华王盼龙丁继胜王永康

(1.山东科技大学测绘科学与工程学院,山东青岛266590;2.自然资源部第一海洋研究所,山东青岛266061)

海洋声速是海洋环境观测的基本要素之一,主要受温度、盐度与压力的影响,准确的声速剖面对各种海洋声学测量均具有重要的意义。大洋声速剖面大部分符合混合层、主跃层与深海等温层的三层剖面结构,具有一定的规律性。目前声速剖面测量主要有直接测量和间接测量两种方法。直接测量法通常采用声速剖面仪直接测量声速,测量精度较高;间接测量通常利用CTD 测量得到的温度、盐度和压力等数据,根据声速经验公式计算得到声速,该方法的精度主要取决于所选择的声速经验公式与仪器精度[1-2]。在大洋科考中,无论是采用直接法还是间接法,全水深声速剖面都需停船定点作业,对于4 000 m 的全水深声速剖面测量,大约耗时5～6 h,采集效率较低,成本较高。在深海多波束海底地形测量过程中,通常采用定点CTD 作业和走航XCTD 相结合等方式获取声速数据,但XCTD 作业深度有限,无法获取全海深声速剖面,易导致因声速数据不准确产生的多波束测量误差,从而影响海底地形成果精度。为有效改正此种原因导致的误差,可以利用声速剖面结构参数化模型实现对声速的有效表示,模型主要分为两类,一类为解析函数模型,另一类为经验正交函数模型[3](Empirical Orthogonal Functions,EOF)。

解析函数模型利用一系列数学表达式及参数表示声速随深度的变化,此类模型的缺点是公式较复杂,应用者需要具备较强的数学基础,不利于推广应用。EOF 函数模型也叫主成分分析法,是描述声速剖面最有效的基函数,其将具有相同特征的声速剖面群进行模态分解,得到基函数,一般3～6个基函数就可以近似表示任意一个声速剖面[4-6]。根据沈远海[6]、张旭等[7]、孙文川等[8]的研究表明,EOF 方法构建浅水声速剖面场具有良好的效果,在构建深远海声速剖面场时的效果研究较少[11]。本文基于东南印度洋海洋调查工作,对获取的CTD 实测数据计算得到的全水深声速剖面进行计算,利用EOF分析方法建立整个作业区的声速剖面场模型;在此基础上,提取深水多波束测量所需声速剖面,对多波束水深地形数据进行声速改正,实验结果表明,通过EOF方法表示的声速剖面可以有效对多波束测量数据进行声速改正。

1 EOF分析法构建声速剖面场原理

设测区有N个实测声速剖面,每个声速剖面有M个均匀深度的声速值,(xi,yi)为声速剖面对应的地理坐标,xi为纬度,yi为经度,将N个声速剖面表示为矩阵形式为[12]：

式中：每一列代表一个声速剖面,每一行代表各个声速剖面同一深度层的声速。

对式(1)中的每一行取平均值,得到所有声速剖面同一深度层的平均声速值,最终得到平均声速矩阵,将声速剖面矩阵与平均声速矩阵相减得到声速扰动矩阵ΔCM×N,进而得到扰动矩阵的协方差矩阵COVM×N：

计算协方差矩阵的特征值λ(λ1,λ2,…,λN)和特征向量V(V1,V2,...,VN)：

λN对应的特征向量VN即为EOF的一个模态,V即为EOF空间函数。

将EOF投影到声速扰动矩阵,得到所有空间特征向量对应的时间系数(主成分)PCM×N：

式中,PCM×N中的每一列为对应声速扰动剖面的时间系数。

声速剖面矩阵可以表示为以下形式：

每一个特征向量对应的特征值表示此特征向量的权重,根据张志伟等的研究,前六阶经验正交函数就可以有效表示声速剖面,因此,本文用前六阶经验正交函数重构声速剖面,表达式如下：

运用双线性插值方法对得到的时间系数进行插值,可得到任意一点的时间系数：

根据最小二乘法原理X=(ATA)-1(ATA),得到待求参数矩阵a4×6。

2 深海声速剖面场建立

2.1 CTD数据预处理

本研究选取东印度洋海洋调查工作中获取的17个CTD 站位数据,其中全水深3个(8、12及13号站位),非全水深14个(测站位置如图1所示)。首先将各站位CTD 测量得到的温度、盐度数据按1 m 深度间隔导出,温度与盐度变化如图2所示,然后再将14个非全水深CTD 的温度、盐度数据拟合计算至4 000 m。

图1 CTD 测站位置Fig.1 Location of CTD stations

图2 温度与盐度变化Fig.2 Changes in temperature and salinity

通过3个全水深CTD 数据分析后发现,该区域海洋温度与盐度在2 000 m 以下变化较小(图2),其中温度我们可将其变化近似为线性变化,可通过有理拟合公式进行拟合计算：

式中：x为深度(m);y为温度(℃);p1,p2,q1和q2为参数。

为验证温度拟合公式的精度,随机选取一个全水深测站所测温度数据,对1 000～2 000 m 温度数据进行拟合并预测2 000～4 000 m 的温度,预测温度误差见图3,可知预测最大误差为0.07℃,引起的声速误差为0.3 m/s,表明运用式(8)可以对温度进行有效的拟合预测。研究区内距离较近的CTD 站位盐度基本相同,可采用邻近的全水深盐度数据对非全水深盐度数据进行替代。通过以上计算,最终得到17组深度为4 000 m、间隔为1 m 的温度、盐度数据。

图3 温度拟合误差Fig.3 The fitting error of temperature

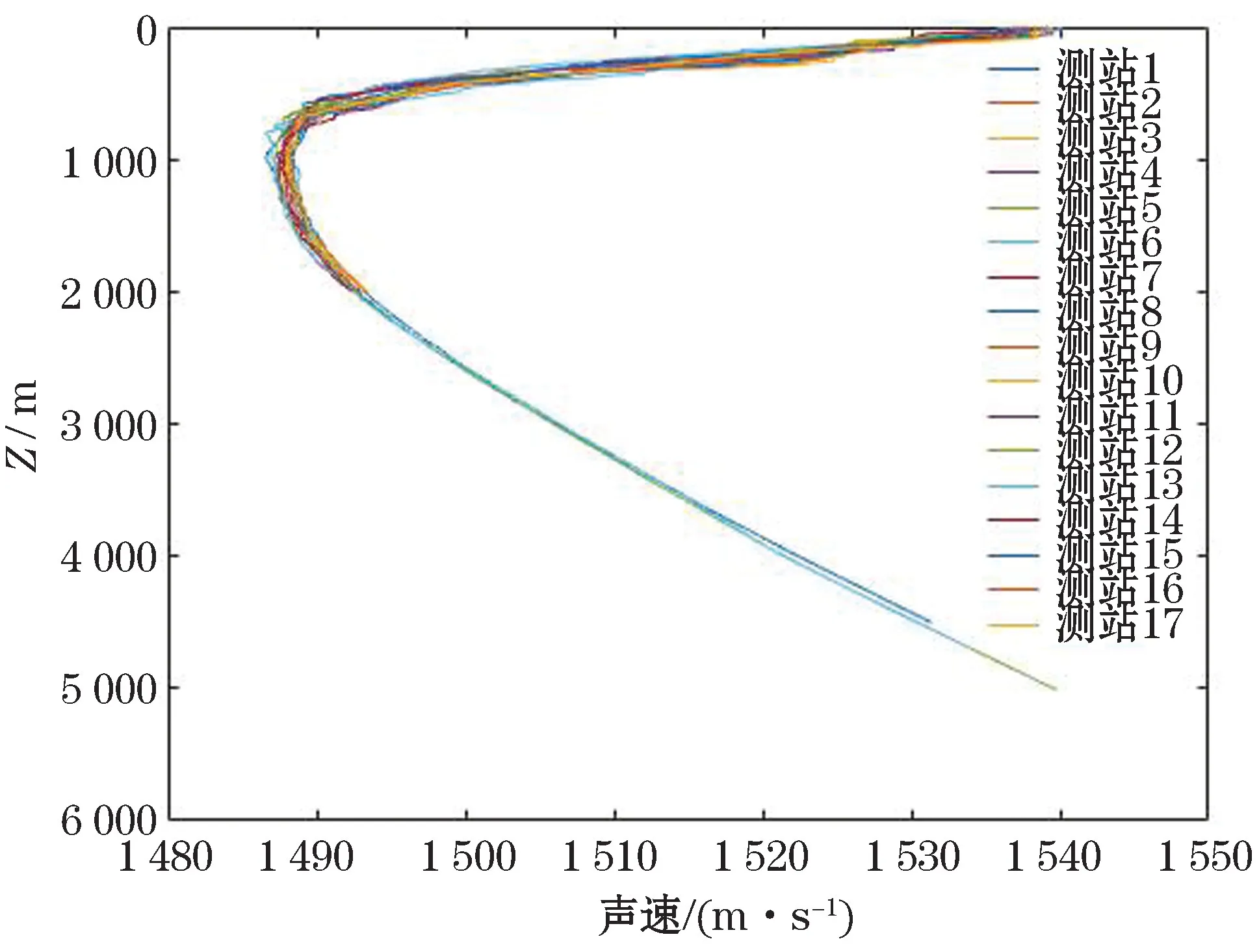
图4 17组声速剖面Fig.4 17 groups of sound velocity profiles

2.2 CTD声速剖面计算

基于CTD 获取的温、盐、深数据,通过声速剖面经验公式可以计算得到各测站声速剖面,目前国内外比较认可的声速剖面经验公式有Chen-Millero[13],Wilson[14],Del Grosso[13-14]及Leroy[15]等,各模型的温度、盐度、压力适用范围有所差别。根据黄辰虎等的研究,Del Grosso、Chen-Millero、C.C.Leroy、Coppens四个声速模型在全球海域具有较高精度及适用性,Del Grosso及Chen-Millero两个模型具有最优精度。在以Del Grosso作为最优模型的假设下,C.C.Leroy公式与Del Grosso公式计算得到的声速差值约为±0.1 m/s,随着水深的增加,互差趋于0.04 m/s,且使用C.C.Leroy 模型计算声速无需测量压力[15-17],为消除对压力数据延伸引起的声速计算误差,本文选取C.C.Leroy 声速剖面经验公式计算声速,C.C.Leroy算法的表达式[15]：

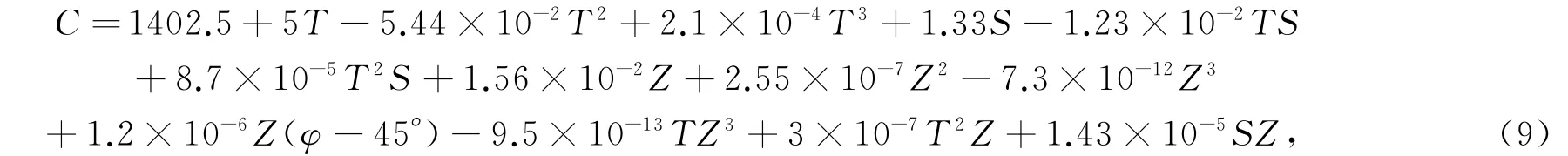
式中：C为声速;T为温度(℃);S为盐度;Z为水深(m);φ为测量处纬度。根据式(9)计算,共得到17组水深为4 000 m,间隔为1 m 的声速剖面(图4)。

2.3 声速剖面的EOF表示

研究区17组声速剖面包含3组全水深声速剖面,14组非全水深声速剖面,本文利用2组全水深声速剖面,14组非全水深声速剖面构建两个声速剖面场,最大水深分别为1 500和4 000 m,站号13的全水深声速剖面数据作为验证。

2.3.1 1 500 m 水深声速剖面场建立

选取1～1 500 m 声速剖面,对所选数据组成的声速矩阵进行经验正交分解,将特征向量按方差贡献率从大到小的顺序进行排列,张旭等[3,7]认为前3～6组特征向量累积方差贡献率为89.4%～96.6%。本文取前6组EOF特征向量构建声速剖面场,前6组特征向量累积方差贡献率为95.01%。用预留全水深声速剖面进行验证,对重构声速剖面与实测声速剖面进行对比,结果如图5。

由图5可知,重构声速剖面与实测声速剖面非常接近,无明显差异点,0～300 m 声速误差逐渐变大,300～700 m 声速误差逐渐变小,700～1 500 m 声速误差无显著变化。声速误差最大值约为4 m/s,声速差值较大处出现在混合层,深度约为300 m,且在混合层差值跳跃较大,这与温度在海水中的变化基本吻合,为验证,对第13组CTD 温度数据求导,结果如图6。

由图6可知,在700 m 以内导数绝对值较大,最大值约为200 m,700～1 000 m 导数绝对值相对较小,1 000～2 000 m 导数绝对值接近0,且基本无变化,2 000 m 以后基本为0,证明温度在700 m 以内变化较快,200 m 左右变化最为剧烈,700～1 000 m 变化逐渐趋于平缓,1 000～2 000 m 匀速下降,2 000 m 以后基本没有变化。混合层由于受光照影响,一天之内同一水深温度变化较大,同一时间垂直方向温度也存在较大差异,在影响声速的3个主要因素中,又以水温变化对声速的影响最大,在深度与盐度不变的情况下,温度变化1 ℃,声速变化约为4.5 m/s。温度变化越快,声速变化也越快,重构声速剖面场所需的特征向量也就越多。本文构建声速剖面场所用声速剖面的声速按照1 m 深度间隔均匀分布,同一深度构建声速剖面场所用声速剖面数相同,在声速剖面数相同的情况下,温度变化越复杂,构建的声速剖面场精度越差,实测声速与重构声速剖面差值也越大。

图5 1 500 m 声速误差Fig.5 Sound velocity errors within a water depth of 1 500 m

经计算,声速误差的标准差为1.383 4 m/s,其中大于3 m/s的数量为63 个,占总数比例为4.2%;2～3 m/s为118个,占总数比例为7.9%;1～2 m/s为527个,占总数比例为35.1%;声速差小于1 m/s的为792个,占总数比例为52.8%,证明利用EOF 方法构建声速剖面场效果较好。

2.3.2 4 000 m 水深声速剖面场建立

选取1～4 000 m 声速剖面,对照构建1 500 m 声速剖面场的方法建立4 000 m 声速剖面场,前6组特征向量累积方差贡献率为94.34%,用预留全水深声速剖面进行验证,对重构声速剖面与实测声速剖面进行对比,结果如图7。

声速误差的标准差为0.880 2 m/s,其中大于3 m/s的数量为64个,占总数比例为1.6%;2～3 m/s为117个,占总数比例为2.925%;1～2 m/s为643个,占总数比例为16.075%;声速差小于1 m/s的为3 176个,占总数比例为79.4%。与构建的1 500 m 声速剖面场进行对比可知,将声速延伸至4 000 m 并不会降低声速剖面场的精度。

图7 4 000 m 声速误差Fig.7 Sound velocity errors within a water depth of 4 000 m

3 重构声速剖面对深水多波束水深数据进行改正

为验证EOF方法构建的声速剖面场对深水多波束进行声速改正的效果,利用构建的4 000 m 声速剖面场,选取同一区域EM122深水多波束测量的6条测线进行声速改正,测线位置如图8所示。其中测线1和测线2水深约为3 000 m、测线3和测线4水深约为4 000 m、测线5和测线6水深约为5 000 m。

图8 多波束测线位置Fig.8 Locations of multi-beam survey lines

测线1实测声速剖面深度为1 500 m,测线2、测线3和测线4实测声速剖面深度为2 000 m,测线5和测线6实测声速剖面深度为4 500 m。为验证本方法的有效性,采用Caris10.0软件进行多波束数据处理,对选取的6条测线分别运用实测声速剖面和EOF方法重构声速剖面进行声速改正,将改正后水深点输出并进行比对,2种声速剖面改正比对结果如图9～11,图中颜色表示差值大小,图中箭头表示测量船的航向。对比对结果进行最大值、最小值、平均值及中误差计算,结果如表1。

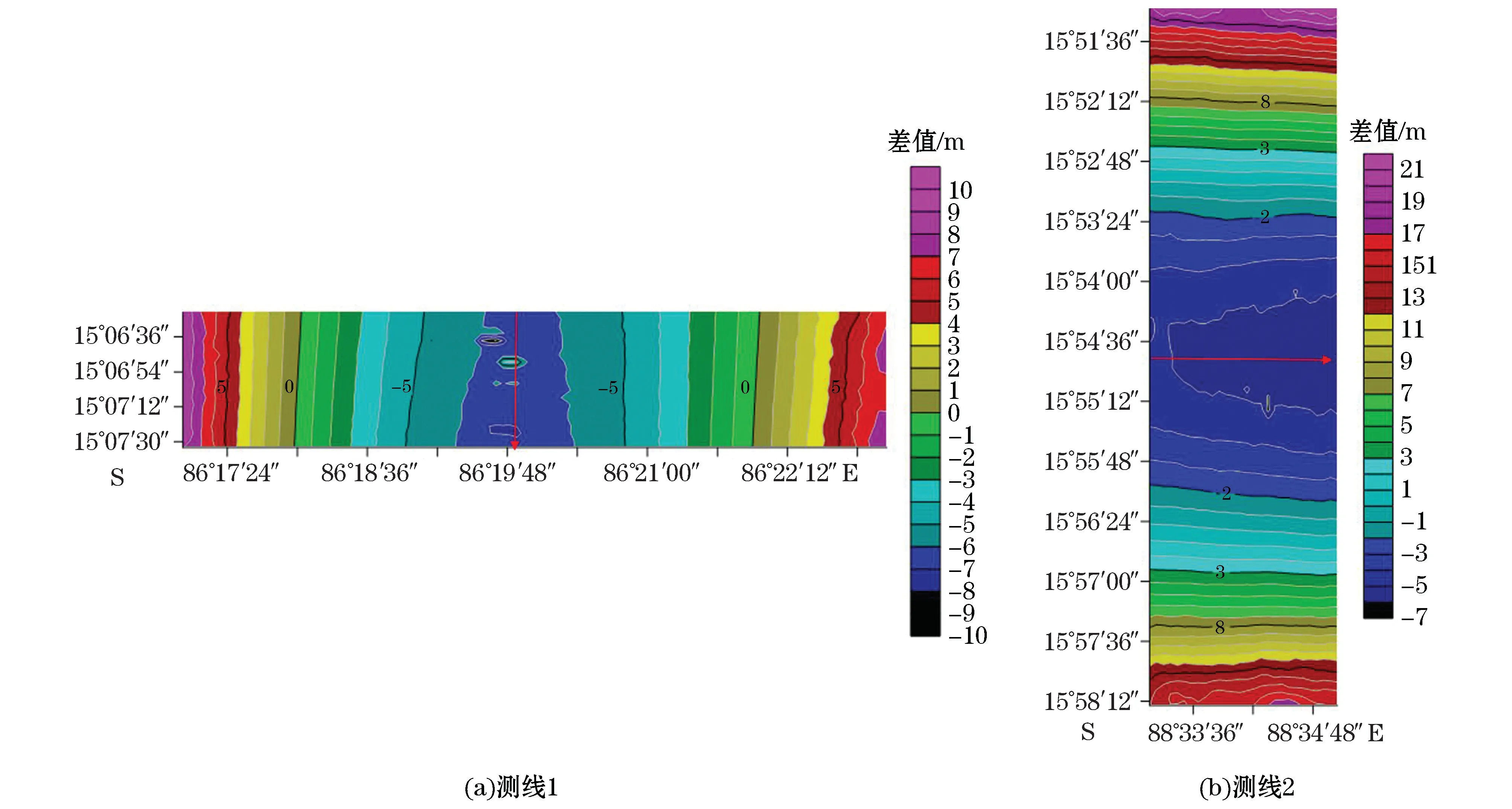
图9 3 000 m 水深差值Fig.9 Differences within a water depth range of 3 000 m

图10 4 000 m 水深差值Fig.10 Differences within a water depth range of 4 000 m

图11 5 000 m 水深差值Fig.11 Differences within a water depth range of 5 000 m

表1 两种声速剖面改正结果误差统计(m)Table 1 Error statistics of the results corrected by using two types of sound velocity profiles(m)

由图11和表1中可知水深约为5 000 m 的测线5和测线6中误差最小,约为0.7 m,相对中误差为0.014%,误差绝对值的最大值约为5 m,相对误差为0.1%,且误差范围为最小,约为2.5 m,测线5和测线6声速改正所用重构声速剖面深度接近实测声速剖面深度,可以认为2种声速剖面深度不同对声速改正结果带来的误差可以忽略不计,误差的主要来源为同一深度层的声速差。测线5和测线6对比的结果表明,通过EOF方法重构声速剖面对多波束数据进行声速改正的结果接近实测声速剖面对多波束数据进行声速改正的结果。

从图10和表1中可以看出测线3和测线4的中误差最大,约为17 m,相对中误差为0.425%,接近《海道测量规范》[18]规定的1%的中误差的一半,误差绝对值的最大值约为58 m,相对误差为1.45%,超过了《海道测量规范》规定的1%的中误差,其误差范围也为最大,约为85 m,这是因为测线3和测线4进行声速改正所用实测声速剖面深度为2 000 m,远小于本文重构声速剖面的4 000 m 深度,用2 000 m 处声速表示2 000 m 以下声速会对水深点最终结果带入较大误差,应用本文方法构建的声速剖面进行声速改正可以有效解决此类问题,提高测量成果精度,对边缘波束的改正效果最为明显;从图9和表1中可以看出水深约为3 000 m的测线1和测线2中误差约为5 m,相对中误差为0.17%,误差绝对值的最大值约为20 m,相对误差为0.67%,误差范围大小约为26 m,大于测线5和测线6,小于测线3和测线4,这是因为测线1和测线2的水深小于测线3和测线4的水深,用声速剖面最大深度点处的声速表示最深点以下声速对水深点结果带来的误差小于测线3和测线4。

综上所述,在5 000 m 范围内,利用EOF方法构建的声速剖面与利用实测声速剖面对深水多波束数据进行声速改正最终得到的水深相差很小,可以满足深远海水深测量的要求。