利用三面角解决一道高三三校联考试题*

广东省佛山市罗定邦中学

广东省佛山市顺德区第一中学(528300)常 艳

在近几年的高考试题中，关于立体几何的考察都可使用两种方法进行求解，即传统几何法、向量法.且在具体的命题过程中还会涉及到翻折问题，其本质是将平面几何的相关知识融入到立体几何中进行考察[1]，传统几何法考察了线面位置关系以及相应的空间角的定义等，对学生空间想象能力的考察更为侧重.向量法体现了用代数的思想解决几何问题，将空间的运算转化为空间向量之间的运算，侧重考察学生的运算能力.在这两种方法之外，本文以一道高三模拟题为例介绍三面角的相关定理，并据此求解立体几何相关问题.

一、题目

题目(2019届高三理科三校(广铁一中、广大附中、广外)期末联考试题第20题)[1]如图1，平面五边形ABCDE中，∠ABC=∠AEC=∠CDE=90°，AC//DE，AE=2，DE=3，将ΔABC沿AC折起，使平面ABC⊥平面ACDE，得到如图2所示的几何体.

图1

图2

(1)求证平面ABE⊥平面BCD；

(2)若二面角C-AB-E的正切值为求二面角A-BC-E的余弦值.

本题从平面几何的相关性质出发，通过翻折形成几何体.关于本题的第一问，注意到图形翻折前后的变化以及面面垂直的判定定理即可求解，具体解答过程可参看文[1]，本文不做详细讨论.本题的第二问是其核心问题，其设问方式是通过二面角信息给出图形中的几何关系，在文[1]中，三位老师分别利用传统几何及向量法对其进行了解答.这两种方法，是我们平时教学的重点，但对于问题本质的揭露还有所欠缺.空间图形——三面角，直接讨论二面角及面角的相关性质，对问题的探究更为直接.现简介如下.

二、三面角简介

如图3，三面角V-ABC是由具有公共端点V的不共面的三条射线V A,V B,V C，以及任两条射线所成的角的内部构成的空间图形.公共端点V称为三面角的顶点，射线V A,V B,V C称为三面角的棱，两棱所夹的平面部分(角)∠AV B,∠BV C,∠CV A称为三面角的面(角).过每一条棱的两个面所成的二面角A-V C-B,A-V B-C,B-V A-C称为三面角的二面角.

图3

三面角的余弦定理三面角的一个面角的余弦，等于其余两个面角的余弦之积加上这两个面角的正弦与这两个面角所夹的二面角的余弦的连乘积.设三个面角V-ABC的三个面角的度量分别为α,β,γ，它们所对的二面角分别为：A,B,C，则有：cosα=cosβcosγ+sinβsinγcosA.

三面角的正弦定理三面角的三个面角的正弦与它们所对的三个二面角的正弦成比例.设三面角V-ABC的三个面角分别为α,β,γ，它们所对的二面角分别为：A,B,C，则

三、利用三面角求解的解法展示

准备工作利用平面几何的相关知识可计算出图1中涉及的所有边长及角度(因与本文的主题无关，所以仅列出最终的结论)，可知

∠EAC=∠ECD=60°，∠ACE=∠CED=30°.

考虑三面角A-BCE，设面角∠EAC,∠EAB,∠CAB分别用α,β,γ表示，其所对的二面角分别用B,C,E表示(二面角C-AB-E即用B表示).根据题干信息可得：由平面ABC⊥平面ACDE得

考虑ΔBAE，则有考虑ΔBEC，则可得则有

考虑三面角C-ABE，设面角∠ACE,∠ECB,∠ACB分别用α,β,γ表示，其所对的二面角分别用B,A,E表示.根据题干信息可得：由平面ABC⊥平面ACDE得

上述解法主要应用三面角的正弦定理，其中很多步骤也可通过三面角的余弦定理进行求解(由读者自行补充)，本文不再赘述.通过上述解法，我们可以清晰地理解各个条件在解题中的作用，例如题干中给出的核心条件“二面角C-AB-E的正切值为旨在推导出ΔABC的信息.我们即可结合三面角的正、余弦定理得到上述条件的等价条件，编制出新的题目供学生练习.

与传统几何法相比，利用三面角求解不需要作出“二面角”(即减少了辅助线)，与向量法相比，减少了坐标系的建立以及相应的计算量.最关键的，利用三面角求解，其基本量为各个面角与二面角，在求解过程中更为直接.

四、与之相关的高考题及改编新题

反思上述解题过程，可以发现本题(以下简称模拟题)的核心图形为三棱锥B-ACE，该模型与2018年高考全国II卷第20题(以下简称高考题)较为相似，现展示如下：

高考真题(2018年高考全国II卷第20题)如图4，在三棱锥AC=4，O为AC的中点.

(1)证明：PO⊥平面ABC；(2)若点M在棱BC上，且二面角M-PA-C为30°，求PC与平面PAM所成角的正弦值.

上题中相互垂直的两个平面ABC及平面PAC，其平面几何的性质为一个等腰直角三角形及等边三角形，与模拟题的图形相比，其将等边三角形转换为有一个角为60°的直角三角形.两题的设问方式也较为相似，都以二面角的信息作为背景，高考题求解线面角，模拟题继续求解二面角.两题的参考答案都是利用二面角信息求解图形中的相关平面几何性质，高考题是为了求得点M的具体位置，模拟题是为了求得BA,BC的长度信息.在文[3]中，笔者以上述高考真题为例，总结出其一般的模型如下：当二面角M-PA-C为θ时，直线PC与平面PAM所成角的正弦值为读者也可尝试利用三面角求解该问题，具体过程请参看文[2].

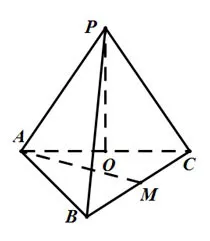
图4

模拟题的新颖之处在于构造了一个五边形，考察了学生们关于平面几何知识的应用，且设计了翻折的过程，考察了学生的动态思想以及轨迹意识.但模拟题中关于ΔDCE的设计较为“多余”，对于核心问题的解决没有帮助，对学生的解题过程还容易产生干扰.笔者认为，在此处高考题的设计更为合理.

下文是根据上面的分析编制出几个变式供读者练习.

变式1 如图5，在三棱锥B-AEC中，AE⊥EC，若二面角B-AE-C的余弦值为求二面角A-BC-E的余弦值.

变式2 如图5，在三棱锥B-AEC中，AE⊥EC，若二面角B-CE-A的余弦值为求二面角A-BC-E的余弦值.

图5