一种改进的小批量手写体字符识别算法

李远沐，王展青

(武汉理工大学 理学院，武汉 430000)

1 引 言

人类往往可以通过学习少量的标注样本就能获得识别某种事物的能力，哪怕是四五岁的孩子，看了几张老虎的图片之后也能准确的识别老虎.而一般的深度学习系统往往需要大量的已标注训练数据才能拥有有限的识别能力，人类和深度学习系统之间的这种显著的差距唤起了人们对小样本学习的研究兴趣[4-6].小样本学习关注的是如何从很少的训练样本中学习到有用的信息，其目的是学习一个在训练样本很少时仍具有良好泛化能力的分类器.目前主流的小样本学习方法大致分为三大类：基于模型的方法[24]，基于度量的方法[5]和基于优化的方法[25].

小样本学习的难点在于由于训练样本很少，难以从中提取出足够的特征来满足模型需要，所以需要充分利用拥有的有限标注样本样本，利用深度学习模型提取其中的“深度特征”.近年来深度神经网络(DNN)的许多巨大突破[1-3]都相当的依赖于规模庞大的标注训练集，小样本领域缺乏足够的样本来更新传统DNN模型中大量的参数，因而无法训练到理想的模型.同时DNN极度依赖网络的训练过程，在训练集较小，网络较深时，极易出现过拟合.而且少量的标注样本并不能代表数据真实的分布，导致得到的分类器方差较大，从而导致模型泛化能力不强，常用的微调(Fine-tuning)技术在小样本学习也会产生过拟合.为了使得少量标注样本得到充分利用，本文引入具有数据高效性的高斯过程模型，同时赋予其深度结构用于提取样本深度抽象特征用于改善模型的推断和学习质量，从理论和实验两个方面来选择合适的模型训练方法.

本文提出了基于深度高斯过程的小样本学习模型，利用多层的高斯过程模型，充分的提取样本深度特征，得到一种改进的基于度量的小样本学习方法，在小批量手写体字符识别领域表现优秀.

2 相关工作

以高斯过程[7]为代表的贝叶斯非参数模型都具有数据高效性的优点，往往只需较少的数据，就能推断出拟合函数的分布情况，而且这种推断一般发生在测试阶段，显著减少了训练阶段的工作量，而且训练得到的模型在测试时仍然可以灵活进行调整.同时高斯过程模型具备很好的度量不确定性的能力，并且Neal[8]早在1998年就证明了单层具有无限节点的神经网络等价于一个具有特定协方差函数的高斯过程.为了使模型同时具有参数模型和非参数模型的特性[17,18]，Damianou和Neil[9]于2013年通过结合深度神经网络和高斯过程提出了深度高斯过程(DGP).深度高斯过程是一种具有类似于DNN结构的深度模型，善于处理抽象特征.相比于标准的DNN，DGP只有少量的核参数和变分参数，因此可以通过少量的训练数据去学习复杂的函数.同时，DGP作为一个非参模型，数据的生成过程不依赖于DNN那样庞大的参数集，而且不同于DNN通过引入非线性函数使得DNN获得处理非线性问题的能力，DGP是通过随机高斯函数的组合自动的获得处理非线性的能力，这种处理能力在针对剧烈变化的数据(数据集越小，数据的波动越明显)时优势尤为明显.同时，DNN的架构往往依赖于主观经验，难以得出最优的选择策略.而DGP因为保留了很多单层高斯模型的优点，比如关于核参数来优化边缘似然函数，有效的避免了过拟合的发生，同时可以自适应的选择网络结构.DGP作为一个贝叶斯模型，拥有许多优良的概率特性，这使得它在小数据集上能有不错的表现.基于以上几点，我们考虑将DGP模型运用于小样本学习，用于提取抽象特征和刻画细节特征.

关于如何训练DGP，因为推断过程中存在一个很难处理的复杂积分，所以DGP的精确推断是不可行的，因此人们提出了许多近似算法[9-12，19-21].变分推断(VI)就是一种常用的近似方法，但是传统的VI往往选择简单的高斯分布作为后验分布的近似分布，因为在大部分的情况真实后验都不是高斯分布，这在很大程度上限制了模型的表达能力.在变分推断框架中，似然函数被分为ELBO和近似后验和真实后验的KL散度，后者往往可以看做是一个正则项，为了改善推断效果，需要尽可能减少这个正则项的影响，一个方法是去寻找更紧的下界[23]，而本文从另一个角度出发，通过寻找更加复杂和灵活的变分分布来减轻正则项的影响.引入标准化流方法(Normalizating Flow[13]),通过对一个简单的分布反复的施加一系列的可逆变换，得到灵活且复杂度可控的后验分布族，结合变分推断方法，得到一个易处理的变分下界，通过优化这个下界来更新核参数和变分参数.

3 高斯过程回归模型

随机过程早已在机器学习领域有了广泛的应用.在具备一些观测数据的情况下，在随机过程的框架下运用贝叶斯规则去推断预测分布，可以使模型具备高效使用数据的能力，而这正好是神经网络所缺乏的.高斯过程(GP)可以由一个均值函数和一个协方差函数完全共同决定(高斯过程存在性定理)，其中协方差函数蕴含了我们对想要建模函数的先验假设,例如光滑性.

设X={xi|i=1,…,N},xi∈d对应的目标值为ti，且T={ti|i=1,…,N}.已知集合D={(xi,ti)|i=1,…,N}，对于新的数据点x′，我们希望找到其对应的目标值t′的预测分布.设目标函数为f，并记FN=[f1,…,fN]=[f(x1),…,f(xN)],以及FN+1=[f1,…,fN+1]=[f(x1),…,f(xN+1)]，其中x′=xN+1.目标函数f的高斯过程先验可以隐式的表示为：

(1)

由多元联合高斯分布的性质，可得预测分布

(2)

其中HN和HN+1是两个归一化常数.ΣN和ΣN+1的关系为

(3)

其中K=[k(x′,x1;Θ),…,k(x′,xN;Θ)]T，Kx′x′=k(x′,x′;Θ)，K为核函数.最后得出预测分布为

p(fN+1|D,xN+1,Θ)=N(KTΣ-1t,Kx′x′-KTΣ-1K)

(4)

4 基于深度高斯匹配网络的小批量字符识别算法

虽然DNN在手写体分类领域取得了巨大的成功，但是当训练数据不足时，由于其海量的参数，DNN很容易产生过拟合现象.DGP相比于DNN，其参数数量要少的多，并且具有贝叶斯性质，是一个很理想的用于小样本学习的模型.我们知道，在机器学习领域，往往都希望训练和测试在完全相同的条件下进行，然而DNN模型的训练过程和测试过程相对独立.针对这两个问题，本文借鉴KNN模型的思想提出深度高斯匹配网络(Deep Gaussian Processes Matching Network)用于小批量手写字符分类.

4.1 深度高斯过程

为了提升神经网络模型的表达能力，引入深度结构，Hinton等人提出了深度神经网络.同样为了改善高斯模型，通过对随机过程而不是函数进行组合，并引入深度结构，Diamianou通过堆叠几个高斯过程模型得到深度高斯过程模型.深度高斯模型是一种包含多个隐藏层的深度有向图模型，并且运用高斯过程来控制层与层之间的映射关系.相比于标准的参数化的深度神经网络中预先给定的非线性函数，深度高斯过程层与层之间的的映射关系有更强的表达能力和数据依赖性(data dependent).而且相较于DNN，DGP模型的参数较少(只有少量的核超参数和变分参数).并且作为一个贝叶斯模型，DGP可以有效的避免DNN中当数据不足时出现的过拟合现象.而从高斯模型中继承到的随机性质，使得DGP能够很好的处理数据的不确定性的问题.

记具有L个隐藏层的DGP模型的输入为x，输出为y，模型定义如下

f1～GP(μ1,k(·)1),h1=f1(h0)+ε1,u1=f1(z0)

(5)

fl～GP(μl,k(·)l),hl=fl(hl-1)+εl,ul=fl(zl-1)

(6)

fL～GP(μL,k(·)L),hL=fL(hL-1)+εL,uL=fL(zL-1)

(7)

有时为了减少变分参数的数量，常常把高斯噪声项置于核函数之内.需要注意的是，每一个高斯函数都有它自己对应的核函数和核参数，故而一层中有可能会出现多个核.此时模型的联合分布为：

(8)

通过对所有的隐变量积分，可以得出作为模型目标函数的边缘似然函数.为简便起见，所有概率分布中都省略了核参数σ.但是所得的仍是一个复杂的积分，使得推断很难进行，所以需要近似的方法，如变分推断[9-11]和期望传播[12].

4.2 余弦距离

余弦距离常常也被称为余弦相似度，是用两个向量之间夹角的余弦作为作为两向量差异程度的度量.当X=(x1,x2,…,xn),Y=(y1,y2,…,yn)时，X和Y的余弦相似度为

(9)

余弦相似度往往对绝对的数值不敏感，而是注重两个向量方向上的差异，即余弦相似度更多的是体现两者的相对差异.

4.3 深度高斯匹配网络

第1步.使用如下结构的卷积神经网络，分别提取测试集和支撑集中图像的抽象特征，将105×105大小的图片扁平化为长度为4096的向量.

图1 本文使用的卷积神经网络结构

第2步.将两个DGP结构作为编码函数，将得到的特征向量嵌入到特征空间中去.然后计算测试图像特征与支撑集中图像特征的余弦距离，完成图像分类，具体如下.

为了得到一个类似于KNN的端到端的手写体字符识别模型，类似于文献[5]，引入注意力核，基于k近邻方法的思想，有:

(10)

其中yi为只有一个维度为1，其余全是0的向量.注意力核为:

(11)

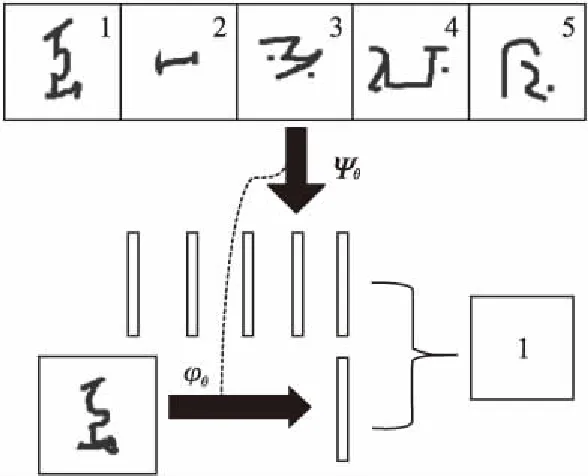
图2 深度高斯匹配网络

其中φ和ψ是由深度高斯过程模型参数化的编码函数，其参数可以通过对训练集分类的准确度进行调整.φ和ψ的作用是提取图像的抽象特征，并将x*和xi嵌入到特征空间中去.

为了确保训练过程和测试过程发生在相同的条件下，首先在原数据集D中采样一个小数据集W，对于W中的每一类，随机的选择K个样本去构造支撑集S，同时随机选择一些样本作为训练集T.由于层与层之间存在复杂的相关性，本文引入伪数据，使用稀疏化方法来简化DGP模型层级之间的相关性.接下来使用随机梯度下降法，通过极大化识别率来更新参数嵌入函数的参数和伪数据的位置，利用log函数为增函数的特点，所得目标函数为:

(12)

模型需要学习的参数有伪点和各层各节点的核参数：

其中L为模型的层数，Dl为第l层的结点数.如果伪输出和伪输入都要学习得到的话，由于更多的参数会提高过拟合发生的几率，模型会损失一部分贝叶斯模型的标准化优势.结合先验信息，我们知道伪点应当与输入点有类似的结构，可以一定程度缓解这个问题.合适的参数初始值可以有效的避免模型陷入局部最优，本文基于最优K均值为所有的输入点聚类，将K个聚类中心作为伪点的初始选择.除了第一层之外，在之后的各层中由于缺乏伪数据的先验信息，而且往往并非简单的标准正态分布，我们假设伪输入采样于一个由标准化流构造的复杂灵活的分布.

为了在下文中阐明模型推断的细节，我们关注特定的模型.为了简便起见，先考虑单层的情况，误差可以通过变分推断方法在层与层之间传播.其层与层之间的推断方式如下，常常将输入x也视为隐变量，记f=f(x)，为了简洁起见，省略伪数据，此时模型的边缘似然函数为：

(13)

变分推断是根据两个分布之间的KL散度值来寻找一个接近真实后验分布的近似后验分布，近似分布往往被限制为一些易处理的分布族，如高斯分布.以这种方式将复杂的推断问题变为极小化分布间KL散度的优化问题.在边缘似然函数中运用Jensen不等式可以获得相同的目标函数，同时假设各个近似分布之间满足均值场假设，即q(f,x)=q(f)q(x).此时，模型的真实边缘似然函数为：

(14)

式(14)中的期望为关于变分分布的期望，两边同时取对数，根据Jensen不等式，有：

(15)

一般情况下，为了计算的简便，都会用一些简单的分布去近似真实的后验分布，而且往往会假设近似分布满足类似于均值场这样的简单结构特征.这在很大程度上影响了变分方法的推断效果，常会导致对预测分布方差的低估，使得做出的决策不可靠，同时，有限容量的近似后验分布族会导致模型参数的MAP估计退化成有偏估计.为了解决这个问题，本文从标准化流方法构造的灵活且任意复杂的分布族中选取近似分布，使得近似分布更有可能接近真实后验分布.

4.4 基于标准化流的DGPMN模型训练方法

由下界可知，我们希望变分分布可以尽可能的接近于真实z的后验分布，但是如果仅仅是基于变分分布为相互独立高斯分布的先验假设或者其他的平均场假设的话，这是很难实现的.事实上，这就是变分方法最大的局限所在，近似分布族不够灵活，哪怕是在一个近似的区域内也无法得到真实后验的一个很好的近似.一个真正理想的变分分布族应该是非常的灵活，并且包含真实后验.标准化流就是通过一系列的可逆变换来对一个简单的密度函数进行转换，最后得到一个更复杂的表达力更强更加复杂的概率分布.

如果我们假设随机变量f的分布函数为p(f)，f′=g(f)，使用反函数定理和链式法则,得到f′的密度分布函数p(f′)为:

(16)

通过这些简单可逆函数的堆叠，我们可以构造出任意复杂的密度函数.

fM=gM…g2g1(f0)

(17)

(18)

之所以这样做除了因为通过对简单分布进行非线性变换后可以得到更复杂的分布之外，由于统计学家LOTUS曾提出，关于变换后分布求期望时，可以不知道变换后的分布的具体形式，仅仅由原始的简单分布和变换函数便可求得这个期望，即:

EpM(fM)[h(fM)]=Ep0(f0)[h(gMgM-1…g1(f0))]

(19)

而且如果h和pM无关的话，还不需要计算雅克比行列式.考虑平面流q(f)=f+v·ρ(wTf+b)，其中参数Ω={w,v,b}.若设ζ(f)=ρ′(wTf+b)，那么此时雅克比行列式：

(20)

那么由初始密度函数q0(f0)通过一系列可逆变换获得的变分分布可以表示为:

(21)

此时，我们用长度为M的流来参数化近似后验分布，即设q(x)≜qM(xM),q(f)≜qM(fM)，可以将式(15)的变分下界写成:

(22)

每一层都以类似的方式进行推断.本文提出的识别算法流程如下，并且在下一节中在真实的数据集上验证了算法的有效性.

算法流程如下所示.

算法1.基于深度高斯过程的小批量手写字符识别算法

参数.模型(核)参数，变分参数

Whilenot convergeddo

X← 小批量训练数据

基于图1的CNN结构初步提取图片特征

利用DGP深度编码图片特征

基于式(10)的注意力核进行特征匹配

x0～q0(x),f0～q0(f)

Endwhile

关于模型中的噪声项，我们发现在优化Damianou[9]给出的目标函数时，由于较强的模型假设，导致模型极易发生噪声退化的情况，即信噪比趋于零.为了缓解这一问题，我们使用聚合性噪声来代替简单的加性噪声[h,ε]即将其也看成隐变量.

5 实验及其分析

为了说明本文模型在小样本手写字符分类问题上的表现，我们在Omniglot数据集上进行实验.其中Omniglot数据集包含来自50个不同地区字母表的1623个手写体字符，每个字符由20个不同的人手写得到.本文的实验平台为python3.6，高斯过程模型基于GPflow平台实现，利用tensorflow的自动求导功能进行参数优化.实验环境为酷睿i5处理器，频率为2.6GHz，RAM为8G.首先，通过误差曲线来对比本文训练算法和传统训练算法的性能.图3显示了训练集和测试集上的基于困惑度的误差曲线，我们发现相比于传统的DGP模型，本文提出的DGPMN模型收敛速度快，而且误差较低.MNIST是常用的手写体数字数据集，图4为将MNIST数据集投影到优化后的二元隐空间的图像，不同类别的数据点用不同的颜色表示，不同类的数据点之间的区分度越大说明隐空间的优化效果越好，结果显示本文训练算法的优化效果较传统DGP好.

图3 训练集和测试集的误差收敛图(左:DGPMN,右:DGP)

图4 二元隐空间投影图

为了说明本文模型的效果，分别使用基于像素匹配的方法(pixels)和经典卷积孪生网络(CNN-S)网络以及本文模型进行多次对比实验.对于Omniglot数据集，我们选择其中的30个地区的字母表作为训练集，其中有964个类.剩余的20个地区的字母表作为测试集，其中有659个类.这意味着测试过程中模型遇到的都是从未见过的样本.训练过程中，每次迭代都从964个类中随机选取20个类，从中选取5个作为支撑集.测试时，从659个类中随机选M个类，每个类提供K个样本来泛化模型，即所谓的M-Way K-shot学习任务，随机猜中正确结果的概率为1/M.结果显示，本文模型在我们比较关心的20通道单样本学习任务中相比于传统的CNN-S网络将预测准确率从88%提高到了94.7%

表1 本文模型在Omniglot数据集上的表现

Table 1 Performance of our model on Omniglot

模型5-way1-shot5-shot15-way1-shot5-shot20-way1-shot5-shotPIXELS41.6%63%38%52%25.1%41.8%CNN-S96.7%98.7%90%95%88%93.4%DGPMN97.8%98.5%94.5%96%94.7%95.5%

在小样本学习中，由于训练集较小，此时，微调网络的结果会比重新训练网络好很多.但是我们发现，本文模型并不依赖于网络的微调操作，这可以有效的避免由微调带来的过拟合现象，实验结果如表1所示,其中N表示未使用微调，Y表示使用了微调.

图5 微调对模型预测Omniglot效果的影响

手写字符图像相对简单，为了进一步说明本文模型的效果，我们在MiniImage数据集上进行实验.MiniImage数据集是从ImageNet数据集中提取出来的一个针对小样本学习问题的数据集，比常用的CIFAR10数据集要复杂.MiniImage数据集包含60000张84×84大小的彩色图片，共100类，每类有600个样本.我们将其中80类作为训练集，另外的20类作为测试集，并进行对比实验，结果表2所示.

表2 本文模型在MiniImage数据集上的表现

Table 2 Performance of our model on MiniImage

模型PIXELSCNN-SDGPMN5-way1-shot22.0%43.2%46.7%5-shot26.1%47.8%56.7%

5 结束语

DGP模型作为一个强大的贝叶斯模型，同时具有信念网络的深度结构和高斯模型的概率性质，在处理小样本手写字符识别问题上有较好的表现.基于采样来训练DGP尽管很灵活，但是难以优化，而且在模型较深时极易陷入局部最优.本文基于标准化流构造灵活的变分分布，同时使用最优K均值聚类方法选择伪点，改善了深度高斯过程模型的训练效果.相比于比较浅的模型，较深的模型一旦训练好必定有更强的预测能力，所以探索更加可行的DGP模型的训练方法是非常有意义的.如何通过并行计算技术提高模型的计算效率也是一个重要的研究方向.