概率生成模型变分推理方法综述

2022-03-09陈亚瑞杨巨成史艳翠赵婷婷

计算机研究与发展 2022年3期

陈亚瑞杨巨成史艳翠王嫄赵婷婷

(天津科技大学人工智能学院天津 300457)

概率生成模型(probabilistic generative model)是知识表示的重要方法，拟从数据集中学习数据概率分布的估计形式.该估计可以是显式的概率密度函数形式，也可以是隐式表示，即不具有显式的概率密度函数，只有生成样本数据的能力[1].具有隐式概率密度函数的生成模型的典型范例是生成对抗网络，这类模型虽然可以生成高质量图像，但是无法获得真实分布的多样性，会导致模式崩塌，同时缺少度量生成模型质量的有效指标[2].具有显式概率密度函数的生成模型通过显式分布建模，该类模型以对数似然函数作为优化目标，可以覆盖数据集上的所有模式，避免模式崩塌问题[1-2].但是在该类模型上求解似然函数一般是难解的，发展了各种近似推理方法，主要包括2类方法：变分推理方法(variational inference methods)[3-4]和蒙特卡洛方法(Monte Carlo methods)[5-6].蒙特卡洛方法通过采样对概率分布进行估计，根据大数定律可知，在采样数目足够多时，蒙特卡洛方法可以很好地估计目标函数，但是存在采样效果严重依赖超参数设置、收敛缓慢等缺点[5-6].变分推理方法把变量求和的概率推理问题转化成优化问题，具有坚实的理论基础、较快的收敛速度、紧致的变分下界，且较容易扩展到大规模数据集，受到研究者的关注[3-4].

对于概率生成模型，变分推理方法通过引入变分分布作为后验概率分布的近似分布，把变量求和或求积分的概率推理问题转化为优化问题，再近似求解该变分优化问题[3-4,7].概率生成模型变分推理方法的发展经历了不同的发展阶段，从开始的指数族(exponential family)分布下具有解析优化表示的变分推理框架[8-12]，到一般概率分布下基于随机梯度的黑盒变分推理框架[13-23]，再到深度模型结构下基于分摊变分推理(amortized variational inference)框架[24-32]，以及基于丰富变分分布的各种结构化变分推理方法[33-45].概率生成模型的变分推理已经被广泛应用于计算生物学、计算机视觉、计算神经科学、自然语言处理和语音识别等领域[3-4,7].

变分推理起源于20世纪80年代，最具代表性的是统计物理学中的均值场方法[8]，20世纪90年代变分推理被机器学习领域研究者广泛关注，并被应用到概率图模型中[9-11].之后，Wainwright教授团队[4]指出，在指数族分布下，结合均值场变分假设，基于坐标上升(coordinate ascent)优化方法可以给出变分优化式的解析表示形式.Bishop教授团队[3]进一步利用指数族分布的条件共轭(conditional conjugate)性质，给出变分贝叶斯优化问题的解析表示形式.但是经典的基于坐标上升的变分推理方法很难推广到大规模数据集，Hoffman教授团队[12]提出随机化变分推理(stochastic variational inference)方法，利用条件共轭指数族分布的自然梯度性质，并结合随机化方法，可以方便将变分推理应用到大规模数据集.条件共轭指数分布族下，结合均值场假设，不需要指定变分分布的形式，利用坐标上升优化方法可以直接给出变分分布及参数后验概率分布的解析表示形式.该类方法可靠性高、优化更新过程收敛速度快，但是条件共轭指数族分布的条件限制了其应用范围，较难应用于复杂模型.

一般的概率生成模型，尤其是深度复杂模型及复合模型，如贝叶斯深度网络、复杂的层次化结构等，都不满足指数族分布条件.针对这类模型，研究者提出了基于随机梯度(stochastic gradient)的黑盒变分推理(black box variational inference)[13-14]，这类方法针对变分优化目标，先计算优化目标的随机梯度，再采用随机梯度方法进行目标优化问题求解.这种基于随机梯度的训练方式可方便应用于复杂概率分布的大规模数据训练中.计算变分优化目标的无偏随机梯度估计是黑盒变分推理的关键任务，同时降低随机梯度的方差使算法有较快的收敛速度是黑盒变分推理算法设计的难点[46].目前最重要的2类梯度计算方法包括评分函数梯度(scoring function gradient)[13]和重参梯度(reparameteration gradient)[15-16].评分函数梯度利用梯度性质及蒙特卡洛采样直接计算变分优化目标的带噪无偏随机梯度，但该方法的方差较大，影响算法性能，后续开展了各种降低随机梯度方差的方法[17-19].重参随机梯度首先对变分分布进行重参转换，再对重参后的目标函数计算梯度[15-16].实践中重参随机梯度比评分梯度的方差小很多，但并没有直接的理论保证[20].但是重参随机梯度的应用范围有限，只能用于连续隐变量，且变分分布形式可表示成位置尺度类分布、累计分布函数可逆类分布，或可以表示成上述2种类型的分布.研究者后续开展了离散型隐变量的重参方法[21-22]，及对于其他类型连续隐变量的隐式重参方法[23]等.基于随机梯度的黑盒变分推理，对概率生成模型分布及结构形式没有限制，但是需要提前建模变分分布结构，通过随机梯度方法求解其变分参数.随机梯度的方差大小直接决定了算法的收敛速度及优化效果，但对于复杂模型，较难直接有效地度量随机梯度的方差，这也是黑盒变分推理算法设计的关键和难点[46].

随着深度神经网络的发展，如何将变分推理应用到深度模型引起了研究者的兴趣.分摊变分推理[24]利用参数化函数，使所有样本点共享变分分布参数，为深度概率生成模型的发展提供了很好的思路[15-16].相比于传统变分推理中每个样本点都具有独立的变分分布参数，分摊变分推理的参数共享方式，可以有效处理深层神经网络，推进了深度概率生成模型的发展.变分自编码(variational autoencoder)模型是深度概率生成模型的典型范例，其概率生成模型采用深度神经网络，其变分分布采用基于分摊变分推理的深度神经网络，并采样基于重参梯度的方法进行模型训练[15-16].之后研究者通过丰富变分分布及生成模型提出了各种改进的变分自编码模型，包括基于隐式分布的变分自编码模型[25-27]、重要加权自编码(important weight autoencoder)模型[28-29]、对抗自编码(adversarial autoencoder)模型[30]、对抗变分贝叶斯(adversarial variational Bayes)模型[31]、像素变分自编码(pixel variational autoencoder)模型[32]等.

基于均值场假设的变分推理极大地简化了优化过程，并得到了广泛应用，上述的指数族分布下具有解析优化式的变分推理，基于随机梯度的黑盒变分推理中的部分算法都利用了均值场假设.但是均值场变分推理存在训练渐进不一致性问题，即当训练样本足够多时，近似后验概率分布仍无法收敛到精确值，使得推理精度受到影响.一直以来各种研究工作通过丰富变分分布来提升变分推理渐进性及推理精度.结构化均值场方法[33-34]结合了传统的均值场方法和精确推理方法，需从模型中识别出易处理子结构，子结构之间采用均值场方法，而子结构内部采用精确推理，这类方法尤其适用于时间序列模型[35-36].标准化流(normalizing flows)方法[37]通过一系列可逆映射将简单的概率密度转换成复杂的概率密度函数，可以提供更紧致的变分界.采用不同的映射函数及结合方法发展出了各种标准化流方法，如平面流(planar flow)、径向流(radial flow)[37]、掩模自回归流(masked autoregressive flow)[38]、可逆自回归流(inverse autoregressive flow)[39]等.层次化变分推理(hierarchical variational inference)模型通过对均值场变分分布的参数引入先验分布增加均值场变量之间的相关性[17].耦合变分推理(copula variational inference)[40-41]通过对均值场变分分布引入耦合分布增加分量之间的相关性.基于混合分布的变分推理利用混合分布的灵活性，提高变分分布结构的灵活性，从而提高变分推理精度[42-43].这类通过丰富变分分布结构提升变分推理精度的方法我们统称为结构化变分推理方法.该类方法通过增加变分分布中隐变量之间的结构信息提升了变分分布的表示能力，尤其对于模型隐变量结构有天然密切相关性模型，如隐Markov模型(hidden Markov models)[35]、动态主题模型等(dynamic topic models)[36]，可以明显提高推理精度，但是模型训练过程中需要更多的计算开销.

本文首先介绍概率生成模型、贝叶斯概率生成模型，及相应模型上的概率推理问题；并介绍了概率生成模型变分推理的一般框架、变分优化问题求解方法，及基于变分推理的模型参数学习过程；然后对于条件共轭指数族模型，给出了基于坐标上升的均值场变分推理，及推广至大数据集的随机化变分推理方法；进一步，给出了结合随机梯度的黑盒变分推理一般框架，并分析了该框架下多种变分推理算法的具体实现；最后综述了结构化变分推理方法，通过不同策略丰富变分分布结构提高变分推理精度；本文最后讨论了概率生成模型变分推理的发展趋势并进行了总结.

1 概率生成模型

本节介绍概率生成模型、贝叶斯概率生成模型，及相应的概率推理问题.

1.1 概率生成模型

概率生成模型又称隐变量生成模型，是一种重要的生成模型，它假设复杂的、可观测向量由简单的、不可观测的隐向量(又称为特征、表示)根据某种模式生成[1-4].概率生成模型的目标就是揭示数据集中蕴含的这种模式，并进一步利用该模型进行数据生成、预测等.

概率生成模型的全概率分布表示形式为

p(x,z)=p(z)p(x|z;θ),

(1)

其中：x∈D表示可观测向量；z∈M表示连续隐向量；p(z)表示隐向量先验概率分布，一般情况下选用高斯分布表示条件概率分布，θ表示条件概率分布参数.

在概率生成模型下，某样本x(i)的生成过程为：首先从隐变量先验分布p(z)中随机生成一个隐向量样本z(i)，然后根据条件概率分布p(x|z;θ)生成样本x(i).概率生成模型中数据生成过程的概率表示形式为

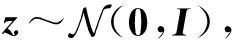
1.2 贝叶斯概率生成模型

对于概率生成模型，若参数θ是随机向量，则称为贝叶斯概率生成模型，此时模型的全概率分布表示形式为

p(x,z,θ)=p(z)p(θ)p(x|z,θ),

(2)

其中：p(θ)表示参数先验概率分布；p(x|z,θ)表示基于参数θ和隐向量z的条件概率分布.此时θ又称为全局隐向量，z又称为局部隐向量.普通概率生成模型的学习任务之一是求解模型参数θ，而贝叶斯概率生成模型是求解参数的后验概率分布p(θ|x).

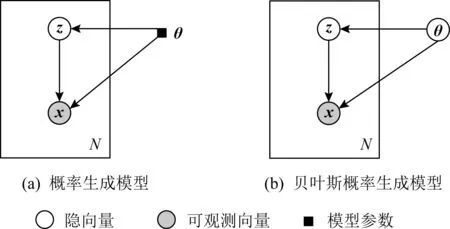
Fig. 1 The graphical models of two models图1 2种模型的图模型结构

概率生成模型的图模型结构如图1所示，其中每个圆形节点表示随机向量，白色节点表示隐向量，灰色节点表示可观测向量，节点之间的有向线段表示变量之间的依赖关系；黑色实心小方块表示模型参数值；方框表示过程可以重复出现，如概率生成模型中，基于隐向量可以重复生成数据样本，观测到N条数据，则该过程重复出现了N次.图1(a)表示一般的概率生成模型，其中参数θ表示参数值，需要通过数据集求解该模型参数；图1(b)表示贝叶斯概率生成模型，其中参数θ表示随机向量，需要根据数据集求解参数的后验概率分布p(θ|x).

1.3 概率推理问题

对于可观测的数据集X={x(1),x(2),…,x(N)}，令Z={z(1),z(2),…,z(N)}表示与观测数据对应的隐变量集合.采用生成模型p(x,z)对该数据集进行建模，数据集的联合概率分布形式为

(3)

此时概率推理问题是根据联合概率分布计算观测数据的边缘概率分布p(X)及隐变量的后验概率分布p(Z|X)，即:

(4)

(5)

进一步，利用最大对数似然可以求解模型参数θ，即:

θ=arg max lnp(X).

对于贝叶斯概率生成模型p(x,z,θ)，需要计算随机变量参数θ的后验概率分布p(θ|x).式(4)(5)中的变量积分是难解的，需要利用变分推理进行近似求解.

2 变分推理一般框架

本节给出概率生成模型的变分推理框架，分析变分优化问题求解方法，并给出基于变分推理的模型参数学习框架.

2.1 变分推理

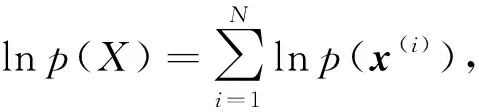
(6)

式(6)中对隐向量求和是难解的，变分推理通过引入变分分布q(z(i))作为后验概率分布p(z(i)|x(i))的近似分布，对lnp(x(i))进行变分变换可得

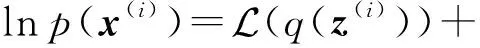
(7)

各部分具体形式为

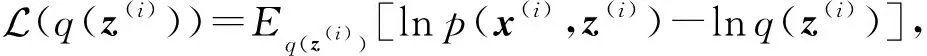
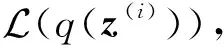
(8)

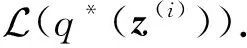
利用不同的概率分布距离度量方式可以得到不同的变分优化问题.基于最小化KL散度DKL(q‖p)的优化问题，又称为基于KL散度距离的变分推理[47]，是最经典的变分转换方式之一，也是本文分析的变分推理的核心.KL散度距离是非对称的，通过最小化DKL(p‖q)也可以构建相应的变分优化问题，这类方法称为期望传播方法[48-49].α-散度距离Dα(p‖q)是KL散度距离的推广，研究者进一步将α-散度距离应用到变分优化问题构建中[27,50-51].f-散度距离Df(p‖q)是更一般化的概率分布距离度量方式[52-53]，其中f表示满足条件的凸函数，不同的f函数定义对应于不同的距离，α-散度距离是其特殊表示形式，研究者将f-散度距离应用于变分推理，给出更灵活的一般化变分优化式.

2.2 变分优化问题求解

求解概率生成模型变分优化问题式(8)的方法，主要包括基于坐标上升的优化方法[9,33]和基于随机梯度的优化方法[13].基于坐标上升的优化方法用于变分分布满足均值场假设的模型，对变分分布的各维分布迭代更新.基于随机梯度的优化方法主要用于变分分布模型结构固定，采用梯度上升方法对变分分布模型参数进行迭代更新.

1) 基于坐标上升的优化方法

均值场变分推理的基本思想是通过假设隐向量各分量之间是相互独立的，从而限定了变分分布的取值空间，简化了优化训练[9,33].具体地，将隐向量z分解成不相交的子向量，记为{zj|j=1,2,…,J}，此时隐向量的变分分布关于子集是边缘独立的，变分分布可以表示成分解形式：

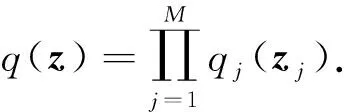
均值场变分优化问题可表示为

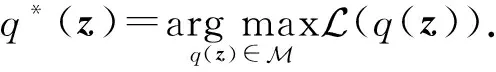
(9)

对于均值场变分推理，可以采用坐标上升算法求解变分优化问题.该算法的基本思想是，对于变分分布的J个分量，每次迭代优化其中的一个分量而固定其他分量.对于分量zj,j=1,2,…,J，通过坐标上升算法可以计算出分量的迭代式为

(10)

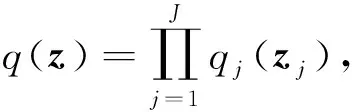
均值场变分推理中只假设隐向量分量是边缘独立的，没有设定其他假设，包括变分分布的表示形式等.基于坐标上升的均值场变分推理实现简单，研究者进一步提出变分消息传播算法[54]，具体地，每个随机隐向量的变分参数利用其Markov毯邻域内隐变量的变分参数进行迭代更新.变分消息传播更新方式结合了变分推理与概率图模型，通过因子图给出了更一般表示形式[49]，并扩展到了非共轭模型[55].

2) 基于随机梯度的优化方法

对于概率生成模型的变分优化式(8)，如果变分分布q(z(i)))的结构形式已知，如高斯分布、基于神经网络结构的高斯分布等，此时变分分布可表示为qφ(z(i)))，其中φ表示变分分布的参数.此时可以采用梯度上升方法求解变分参数φ，即：

2.3 基于变分推理的模型参数学习

对于概率生成模型p(x,z)，通过最大化数据集的对数似然函数lnp(X)，计算模型参数θ是概率生成模型的重要学习任务[56].期望最大化(expectation maximization, EM)算法是求解含有隐向量模型参数的基本方法，通过迭代执行E步(expectation step)和M步(maximization step)计算模型参数，其中E步是利用上一步的参数计算隐向量后验概率分布，M步是利用隐向量知识求解模型参数.变分推理与EM算法有着天然密切的联系[1]，当E步无法精确计算隐向量后验概率分布时，需要借助变分推理进行近似求解.

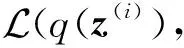
对于该优化问题，分别关于参数θ和变分分布q(z(i))迭代求解直到收敛，可以计算出模型参数θ及自由分布q(z(i)).该求解过程称为变分EM算法，其中变分E步用于求解变分分布q(z(i))，变分M步用于求解模型参数θ，迭代执行变分E步和M步直到收敛.变分EM算法的具体过程：

变分E步为

变分M步为

对于贝叶斯概率生成模型p(x,z,θ)，需要计算参数的后验概率分布，在均值场变分假设下，变分分布形式为q(z,θ)=q(z)q(θ)，观测数据的证据下界为

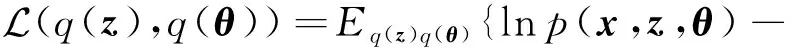
此时通过变分EM算法交替更新自由分布q(z)，q(θ)，具体过程：

变分E步为

i=1,2,…,N；

变分M步为

最终得到隐变量后验概率分布的近似分布q(z)，及隐变量后验概率分布的近似分布q(θ).

3 条件共轭指数族下的变分推理

指数族分布是一类重要的概率分布表示形式，包含高斯、伯努利分布、多项式分布等多种分布.条件共轭指数族是指对指数族分布参数引入与似然函数共轭的先验分布，从而使得参数后验分布具有与先验相同的分布形式[4].对于条件共轭指数族分布，基于坐标上升算法可以给出变分优化问题的解析表示形式，并且结合随机优化策略可以将变分推理推广到大规模数据中.

3.1 条件共轭指数族分布

指数族分布下概率生成模型的概率分布为

p(x,z|θ)=h(x,z)g(θ) exp {θTu(x,z)},

(11)

其中：θ称为自然参数；u(x,z)为充分统计量；g(θ)为归一化项；h(x,z)为基测度.参数θ的共轭先验为

p(θ;α1,α2)=f(α1,α2)g(θ)α2exp{α2θTα1},

(12)

其中，f(α1,α2)表示归一化量.观测数据集X的联合概率分布为

(13)

对隐向量及模型参数引入均值场变分分布q(Z,θ)，即：

(14)

条件共轭指数族分布下的变分优化式为

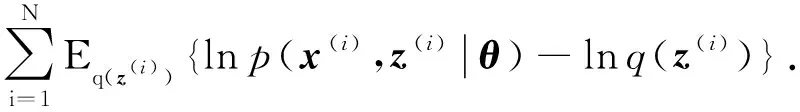
(15)

3.2 基于坐标上升的优化问题求解

对条件共轭指数族分布的变分优化式(15)，采用坐标上升算法进行优化求解，隐向量的变分分布q(z(i))的迭代更新式为

q(z(i))=h(x(i),z(i))g(E[θ])exp{Eq(θ)[θT]×
u(x(i),z(i))},i=1,2,…,N.

(16)

参数的变分分布q(θ)的迭代更新式为

q(θ;λ1,λ2)=f(λ1,λ2)g(θ)λ2exp{θTλ1},

(17)

其中：

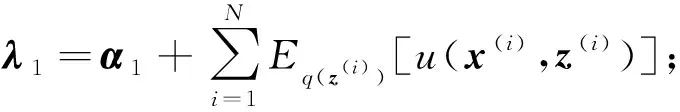
对于条件共轭指数族分布，在引入隐变量自由分布过程中，不需要给出自由分布的具体形式，利用坐标上升方法可以直接给出自由分布的分布形式及参数更新式.对比式(12)(17)可知，参数变分分布q(θ;λ1,λ2)与先验分布p(θ;α1,α2)具有相同的分布表示形式.通过迭代执行局部隐变量变分分布更新式(16)和全局参数变分分布更新式(17)，直到算法收敛，计算出目标函数.对于条件共轭指数族分布，基于坐标上升的变分推理的执行过程如算法1所示：

算法1.基于坐标上升的变分推理.

输入：数据集X、模型p(X,Z,θ)、变分分布q(Z,θ)；

输出：自由分布q(θ;λ)，q(z(i)),i=1,2,…,N.

repeat：

for数据点x(i)∈X

根据式(16)更新变分分布q(z(i))；

end for

根据式(17)更新自由分布q(θ)；

until满足收敛条件.

3.3 随机化变分推理

对于条件共轭指数族分布，采用基于坐标上升的变分推理进行模型训练，每次需要遍历整个数据集才能更新一次模型参数，模型训练效率不高，较难推广至大规模数据集上.针对该问题，Hoffman教授团队[12]提出了随机化变分推理方法，将随机优化技术应用到变分优化目标，并利用指数族自然梯度的性质，得到迭代更新式，使变分推理可以应用于大规模数据集[12,57].

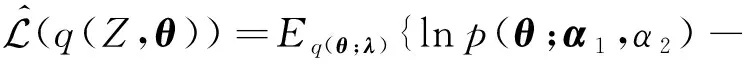
(18)

根据条件共轭指数族的自然梯度的性质，详细公式推导可参考文献[12]，可求解该变分优化式关于超参λ的带噪无偏自然梯度为

再根据随机梯度上升方法得到自由分布超参数的迭代更新式，即：

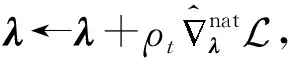
(19)

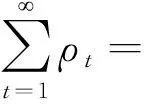
随机化变分推理中的批处理数据集XS，其中S表示批处理的规模，一般满足1≤S≪N.当S值较大时可以降低随机自然梯度的方差，但是为了更容易扩展到大规模数据集，必须让批量处理规模远远小于数据集规模，即S≪N.随机化变分推理算法更新过程如算法2所示：

算法2.随机化变分推理.

输入：数据集X、模型p(X,Z,θ)、变分分布q(Z,θ)；

输出：自由分布q(θ;λ).

repeat：

采样j～Uniform(1,2,…,N)；

根据式(16)更新变分分布q(z(j))；

根据式(19)更新变分分布q(θ;λ)；

until满足收敛条件.

在线变分推理(online variational infernce)[57]与随机化变分推理具有相同的参数更新方式，其中随机化变分推理的批处理样本集XS是从样本集X中均匀随机采样，在线变分推理假设批量数据集XS是已知的，比如在流应用中，假设某数据源可以顺序产生批处理数据集.随机化变分推理的学习率及批处理大小会影响算法的收敛速度.根据大数定律可知，增加批处理规模，可以降低随机梯度噪音，允许较大的学习率.提高随机化变分推理收敛速度，可以通过固定学习率自适应选择批处理数据规模[58]，或者通过固定批处理规模自适应选择学习率[59-60].同时，随机化变分推理的梯度方差决定了算法的收敛速度，较小的梯度方差使算法具有较快的收敛速度.可以通过降低随机梯度方差来提高随机化变分推理的收敛速度，包括通过引入控制变量降低随机梯度方差[61-62]，通过非均匀采样，如重要采样(important sampling)[63]、分层采样(stratified sampling)[64]、基于聚类的采样(clustering-based sampling)[65]、多元批采样(diversified mini-batch sampling)[66]等，选择具有较小方差的批处理数据来降低梯度方差.

4 黑盒变分推理

本节针对一般概率生成模型，综述基于随机梯度的黑盒变分推理方法，该方法首先通过计算变分优化式的随机梯度估计，再结合随机梯度更新变分分布参数，具有广泛的应用范围，并可以方便应用到深度复杂模型及大规模数据[13-14].

4.1 黑盒变分推理框架

对于一般的概率生成模型，假设变分分布q(z)的分布形式是固定的，训练过程只需求解变分分布参数φ.此时变分推理模型可表示为q(z;φ)，样本点x(i)的变分下界为

其中,期望Eφ(i)[·]表示关于自由分布q(z(i);φ(i))的期望.数据集X的对数似然函数lnp(X)的变分优化问题为

算法3.黑盒变分推理框架.

输入：X，p(x,z)；

输出：自由分布q(z(i);φ(i)),i∈{1,2,…,N}.

初始化参数φ(i),i∈{1,2,…,N}；

repeat：

学习率ρt;

forx(i)∈X

end for

until满足收敛条件.

随机梯度估计方法主要是基于蒙特卡洛的估计方法，典型方法包括基于评分函数的随机梯度[13]和基于重参的随机梯度[15-16].随机梯度的噪音或方差控制是这类方法的难点，会直接影响算法的收敛及收敛速度.基于随机梯度下降的方法对步长很敏感，步长太大会使算法不收敛，步长太小会使算法收敛速度特别慢.针对这些问题研究者提出各种随机优化框架，如Adagrad[67],Adam[68],RMDProg[69]等，可以根据当前或过去的梯度值自适应地确定更新步长.

4.2 基于评分函数的随机梯度

4.3 基于重参的随机梯度

基于重参的随机梯度首先对变分分布进行变量变换，此时变分分布由噪音分布经过带参数的确定性函数转换得到，然后对重参后的目标函数求梯度[15-16].对于变分分布q(z;φ)，通过引入噪音分布ε～p(ε)，并基于参数φ设计从ε到z的确定性映射函数S，对变分分布实现重参，即：

ε～p(ε),
z=S(ε;φ)，

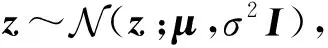
利用重参映射函数对变分优化式进行变量替换，并通过蒙特卡洛采样，可计算出变分下界的带噪无偏估计：

其中：L表示采样的个数；z(i,l)表示通过映射函数S获得的样本，即：

z(i,l)=S(ε(l);φ(i)),ε(l)～p(ε),

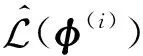
该梯度称为基于重参的随机梯度.

相比基于评分函数的随机梯度，基于重参的随机梯度在实践中具有较小的梯度方差，但是并没有严格的理论证明[20]，研究者开展了特定结构下重参梯度的方差分析研究[46,71].基于重参的方法需要找到一个从噪音向量ε到隐向量z之间的映射S，重参方法适用于3类概率分布：1)位置尺度类概率分布;2)具有可逆累计分布函数的概率分布;3)通过变换可以表示成上述2类的概率分布分布[15].对于不满足上述条件的连续隐向量，研究者提出隐式重参梯度(implicit reparameterization gradients)方法，利用从z到ε累计分布函数的梯度，结合链式规则求变分下界的随机梯度[23].对于离散隐向量，研究者采用gumbel-max技巧，并利用softmax操作代替argmax操作，实现离散变量重参[21-22].

4.4 分摊变分推理方法

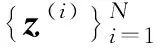
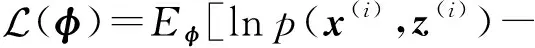
其中，fφ(x)表示基于样本的参数化函数；φ表示变分分布模型的共享参数.分摊变分推理的共享变分参数训练是基于所有样本累计训练的结果，相比传统每个样本独立的变分参数方式，该训练方式又称为有记忆的训练模式.传统变分推理中独立变分参数如图2(a)所示，分摊变分推理中分摊变分推理参数如图2(b)所示，其中，实线箭头表示生成过程，虚线箭头表示推理过程.对于分摊变分推理对应的优化问题，可以采用基于评分函数的随机梯度或基于重参的随机梯度进行迭代求解.

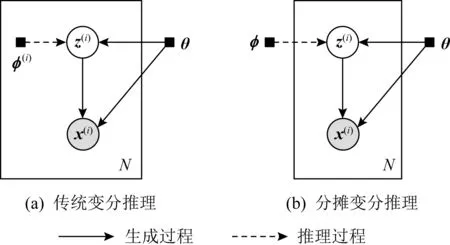
Fig. 2 The graphical models of two inferences图2 2种推理的图模型结构

4.5 范例：变分自编码模型

变分自编码模型由Kingma[15]和Rezende[16]这2个研究团队于2014年分别独立提出的，是当前最经典的深度生成模型之一，它有效结合了概率生成模型和深层神经网络.具体地，变分自编码的生成模型p(x|z;θ)结合了深层神经网络，变分推理模型采用分摊方式q(z|x;fφ(x))，其中函数fφ(x)也采用深层神经网络.在模型训练中，采用基于重参的随机梯度对生成模型参数θ及变分推理模型参数φ同时进行训练学习.

对于单样本x(i)，变分自编码的变分下界为

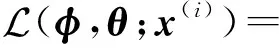
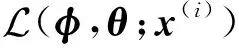
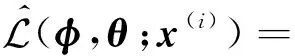
其中：z(i,l)表示根据蒙特卡洛采样及映射函数得到的样本，即z(i,l)=S(ε(l);φ),ε(l)～p(ε).对于数据集X，基于批处理的数据集XR的变分下界为

此时可以方便计算出变分下界关于变分参数φ

变分自编码模型以其简单的训练方式和较好的实践效果很快成为深度生成模型的研究焦点[44].相关研究工作主要集中在丰富变分推理结构、提高变分界的紧致性、提高生成图像质量、研究变分隐空间的解耦特性等方面.研究者提出将隐式分布应用到变分分布中增强变分分布表示能力[25-27].进一步针对隐式变分分布中KL散度项难以求解的问题，提出结合对抗网络的判别函数进行优化求解的方法[27,31].为了提高变分下界的紧致度，研究者提出重要加权变分自编码[28-29]，通过从变分分布中进行多次采样构建变分下界，采样次数越多，变分界越紧致.同时，研究指出通过丰富生成模型，如引入丰富的隐变量先验分布，提高深度生成模型变分下界的紧致性[72]，对先验分布引入高斯混合丰富模型结构[73].针对似然函数在各维度上的分解形式引起的模型性能的降低，提出像素变分自编码[32]，通过条件分布保留像素之间的相关性，提高变分界精度.针对变分自编码模型生成图像模糊的问题，很多研究团队开展了研究.其中，英伟达研究团队提出矢量量化的变分自编码(vector quantized variational auto-encoder)[74]，将PixelCNN引入隐变量先验分布，并利用多尺度层次化建模方法生成高质量图像;进一步对于变分自编码模型，通过使用残差块和批正则化精心设计神经网络结构生成高质量图像，同时保留了变分下界[75].针对变分自编码模型的解耦统计性分析，研究者开展了相关分析，通过加入不同的正则化方法对变分隐空间进行解耦，提升可解释性[76-79].

5 结构化的变分推理

均值场变分推理假设变分分布各分量是边缘独立的，这种假设可以简化推理，但是损失了推理精度.结构化的变分推理是指通过各种方法增加变分分布分量之间的相关性，提高推理精度.本节综述通过各种不同方式增加变分分布分量之间相关度的结构化变分推理方法.

5.1 结构化均值场方法

结构化均值场方法(structured mean field approach)首先由Saul和Jordan等人提出[11]，该方法结合了传统的均值场方法和精确推理方法，首先从概率生成模型中识别出易处理的子结构，如链式结构、树型结构等，然后在各子结构之间执行均值场变分推理方法，而在每个子结构内部执行精确推理，如junction tree方法[34].该方法需要根据模型的具体情况人工选取易处理的子结构.如对于概率生成模型，选择的J个易处理子结构可记作{zj|j=1,2,…,J}，此时变分分布表示为

其中，变分子分布{q1(z1),q2(z2),…,qJ(zJ)}之间是条件独立的，对于每个子结构qj(zj)内可以精确计算单变量边缘概率分布.

之后，结构化均值场方法得到了进一步发展[34,80-81]，并结合黑盒变分推理方法应用于大规模数据的更新[82].该方法尤其适合于时间序列模型，如隐Markov模型[35]、动态主题模型[36]等，此时采用的变分分布显式保留了时间点之间的结构信息，而其他变量之间仍旧是边缘独立的.

5.2 标准化流方法

标准化流方法[37]是构建丰富变分分布的一类重要方法，可以给出更紧致的变分界.该类方法通过一系列可逆函数将一个简单的变分分布，如均值场变分分布结构，转换成结构更丰富的变分分布.

令z表示连续随机向量，其概率分布为q(z)，f:d→d表示映射函数，通过f对隐向量z进行变量变换z′=f(z)，变换后的随机向量z′的概率分布为

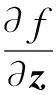
zK=fK∘…∘f2∘f1(z0),

利用变换后的分布作为变分分布，即q(z(i)))=qK(zK)，此时的变分下界为

L(φ)=Eq0(z0)[lnp(x,zK)-lnqK(zK)].

选用不同的映射函数可以得到不同的标准化流方法，平面流和径向流是2种最经典的标准化流，其中每次映射可以看作一个隐层单元，其雅可比行列式可以很方便计算，一般应用于低维隐空间[37].Sylvester标准化流是平面流的一般化表示，克服了单一隐层的缺点，丰富了变分分布的表示能力[83].自回归流是一种结构丰富同时雅可比行列式容易计算的映射函数，成为标准化流的研究特点之一，不同的结合方式形成不同的算法，包括real non-volume preserving flows[84]、掩模自回归流[38]、可逆自回归流[39]等.

5.3 其他结构化变分推理

除了结构化均值场方法、标准化流方法之外，研究者还提出了各种其他策略，通过丰富变分分布结构提升变分推理精度.

1) 层次化变分模型.均值场方法假设变分推理模型各维度之间是相互独立的，层次化变分模型[17](hierachical variational models)通过引入贝叶斯方法丰富模型结构，对变分参数引入先验分布，增加变量之间的相关性.该方法在保持隐变量之间条件独立性的同时，丰富了变分推理模型结构关系.对于观测向量x，基于完全均值场变分推理中变分分布为

层次化变分推理通过对变分参数φ引入先验分布q(φ;λ)，此时层次化变分推理模型为

2) 耦合变分推理.耦合变分推理[40-41]通过对均值场变分分布引入耦合分布增加分量之间的相关性，此时变分分布形式为

Q(z2),…,Q(zd)),

其中,c表示耦合函数，即基于各分量边缘累计分布函数Q(z1),Q(z2),…,Q(zd)的联合概率分布.

3) 基于辅助变量的变分推理模型.在隐变量生成模型中引入附加向量a,此时生成模型概率分布形式为

p(x,z,a)=p(z)p(x|z)p(a|x,z).

变分推理模型的形式为

q(a,z|x)=q(z|a,x)q(a|x).

此时，观测样本x对应的变分下界为

4) 基于混合分布的变分推理.混合模型具有灵活的表示形式，从20世纪末开始已经被应用到变分推理模型中[42-43].混合模型灵活的结构形式也意味着复杂的变分推理，研究者提出了各种训练方式，包括基于辅助界的方法[17]、固定点更新方法[85]等.受到boosting方法的启发，最近发展了boosting变分推理方法[86]及变分boosting方法[87]，通过每次只更新其中一个分量，而固定其他分量的方式进行训练.

6 研究展望

概率生成模型变分推理已经成为人工智能领域的研究热点，该方向进一步研究工作主要包括4个方面：

变分推理的理论研究工作还非常有限，已开展的部分理论研究工作主要集中在变分推理统计性质分析方面，包括对变分贝叶斯推理中模型参数的训练一致性分析[88]，如贝叶斯线性模型参数训练一致性的分析[89-90]、泊松混合效应模型参数渐进正态性的分析[91]、随机区块模型参数渐进正态性的分析[92]等.相比蒙特卡洛近似推理理论研究，变分近似推理的理论研究还有很多工作有待深入，包括变分推理近似误差的量化、基于变分推理的预测分布的统计性质等.

变分推理通过概率分布距离度量来构建变分优化式，根据不同的距离度量方式可以得到不同的变分优化式，当前变分推理主流是基于DKL(q‖p)散度的变分优化问题开展研究.研究者也开展了基于其他概率分布度量的变分推理研究，包括DKL(p‖q)散度距离[48,93]、α-散度距离Dα(p‖q)[94]、f-散度距离Df(p‖q)[53,95]等.但是这方面研究的深度不够，包括如何基于这些概率分布距离度量设计收敛速度更快的优化算法、如何丰富变分分布结构、如何有效地同深度神经网络相结合处理大规模数据等，这些研究问题都是有待深入探讨分析的.

基于采样和基于变分的推理方法是两大类重要的近似推理方法，基于采样的近似推理方法，精度较高且有理论保证，但是收敛速度慢，且受先验参数影响；基于变分的近似推理方法收敛速度快，但是推理精确不易量化.研究如何将2类近似方法进行有效地结合，实现近似推理精度与计算速度的权衡折中是一个重要的研究方向.已开展的相关研究包括：将Metropolis-Hastings采样引入已训练的变分分布[96]、利用MCMC进行近似求解变分推理的坐标上升优化成果[97-98]、引入变分近似方法到MCMC链中[99]等.进一步深入研究采样方法和变分方法的结合方式及结合场景对机器学习领域都有重要的理论价值和实践意义.

深度概率生成模型结合了概率生成模型和深度神经网络，是深度模型的重要构成部分.得益于黑盒变分推理方法的发展，可以方便地开展深度概率生成模型在大规模数据集上的训练.基于变分推理的深度概率生成模型也是深度学习方面的研究热点.随着大规模数据集规模及算力的进步，深度学习在实际应用中取得了很多瞩目成果，但是理论研究方面发展缓慢.可以以深度概率生成模型为切入点，基于变分推理开展相关理论研究，如深度特征表示、隐变量可解释性等.深度概率生成模型的2类典型范例是变分自编码和生成对抗网络.变分自编码是针对显式深度概率生成模型进行训练，模型具有生成数据及特征表示能力；而生成对抗网络是针对隐式深度生成模型进行训练，模型仅具有生成高质量数据的能力.针对不同的应用场景或模型结构，如何扬长避短将2类方法有效结合起来是一个重要的研究方向.已有的相关研究工作包括对抗自编码模型[30]、对抗变分贝叶斯[31]等，是将对抗策略引入到变分优化式的求解中.但是这方面仍旧有很大的研究空间.