三种常用周跳探测与修复方法的性能分析
2020-11-18夏思琦于先文齐晨
夏思琦,于先文,齐晨
(东南大学 交通学院,江苏 南京,210000)
0 引 言
载波相位测量技术是目前精度非常高的全球卫星导航系统(GNSS)测量定位方法.在获得载波相位观测值的过程中,由于受到外界环境等因素的影响,会造成接收机整周计数器发生中断,从而导致载波相位观测值发生整周跳变,这个整周跳变被称作周跳.载波相位测量定位精度的高低与是否对载波相位观测值进行了准确的周跳探测与修复有直接联系.
随着多频、多系统GNSS定位技术的发展,目前已有多种周跳探测与修复方法被提出.Lichtenegger[1]提出了利用多项式拟合法进行周跳探测与修复,该方法通过判断拟合值与实测值的差值大小以实现对周跳的探测与修复;TurboEdit方法[2-3]是基于双频组合观测值的周跳探测方法中较为经典的方法,其原理是利用双频载波相位观测值和伪距观测值构造的MW(Melborne-Wubbena)组合和GF(geometry-free)组合观测值联合探测周跳,该方法具有探测可靠性高的优点;黄令勇等[4]提出通过构造三频无几何相位组合进行周跳探测,
并利用整数最小二乘方法进行搜索固定以实现对周跳的修复,该方法对于三频数据具有很好的周跳探测与修复效果.
多项式拟合法、TurboEdit方法、三频无几何相位组合法是常用的周跳探测与修复方法,评价及比较这三种方法的性能,对深入认识和合理选用周跳探测方法具有重要的意义.
1 周跳的产生及常用探测方法
1.1 周跳的产生
当某一历元无周跳发生时,原始载波相位观测方程可写成[5]:
λiφi=ρ+c(δTr-δTs)-Ii+ρtro+
mr-ms-λiN+ε,
(1)
式中:λi表示载波Li对应的波长(i代表频率编号);ρ表示星地间的几何距离;Ii为载波Li对应的电离层延迟;ρtro表示对流层延迟;δTr、δTs分别代表接收机r和卫星s的钟差;c为真空光速;mr、ms分别为接收机r和卫星s的相位硬件延迟;ε表示观测噪声.
当接收机在连续跟踪卫星信号时,由于某种原因会导致卫星信号短时间失锁,失锁期间整周计数器中断,使得计数器整周计数Int缺失了ΔN周,这个缺失的周数即为周跳.于是从该历元开始,以后各历元均包含周跳ΔN.在发生周跳的情况下,式(1)应写成
λiφi=ρ+c(δTr-δTs)-Ii+ρtro+dr-
ds-λiN-λiΔN+ε.
(2)
周跳对定位的影响很大,文献[6]指出,即使只发生一个周跳,也会对定位结果造成分米级的影响,因此,必须要对周跳进行准确探测与修复.
1.2 几种常用的周跳探测方法
1.2.1 多项式拟合法
利用多项式拟合法探测周跳,其多项式一般形式为[7]:
φu=a0+a1(tu-t0)+a2(tu-t0)2+…+
an(tu-t0)n,
(3)
式中,u=1,2,…,m,m>n+1.
使用多项式拟合法进行周跳探测的大致流程为:首先使用m个已知不含周跳的相位测量观测值进行拟合,得到其对应的n阶多项式及相应参数;然后根据多项式和参数拟合出下一个观测值;最后用拟合值与实测值比较,以此来发现周跳并修正载波相位观测值.
1.2.2 TurboEdit法
TurboEdit法[3]主要是利用双频载波相位观测值和伪距观测值构造MW和GF组合观测值进行周跳探测与修复.MW组合周跳检验量为

(4)
式中:φ1、φ2和P1、P2分别为f1、f2频段上的相位观测值和伪距观测值;λWL和NWL分别表示宽巷波长和宽巷模糊度.
若满足如下两个条件[3],则认为当前历元存在周跳:

(5)

GF组合周跳检验量为
LGF=λ1φ1-λ2φ2-(P1-P2).
(6)
若满足如下两个条件[3],则认为当前历元存在周跳:

(7)
当探测某一历元发生周跳时,可联合两种组合观测值建立误差方程组,并通过对误差方程组求解获得各频点上的周跳值.
1.2.3 三频无几何组合法
根据多频理论[8],记α、β、γ为组合系数且α+β+γ=0,得到无几何相位组合
αλ1φ1(t)+βλ2φ2(t)+γλ3φ3(t)=
ηI1+Nαβγ(t)+ε(t),
(8)
式中:η为电离层延迟放大系数;Nαβγ为组合模糊度.
当周跳发生时,无几何相位组合历元间差值可表示为
αλ1Δφ1+βλ2Δφ2+γλ3Δφ3=-ηΔI1+
Δε+αλ1ΔN1+βλ2ΔN2+γλ3ΔN3.
(9)
若满足如下两个条件则认为当前历元存在周跳:
|αλ1Δφ1+βλ2Δφ2+γλ3Δφ3|≥lσ(α,β,γ),
(10)

将组合观测值在历元间差分,并建立误差方程组进行求解,获得各频点上的周跳实数解及方差阵,再采用整数最小二乘方法[9]获得周跳整数解.
2 周跳探测性能评价方法

ΔN∈Zn={z1,z2,…,z∞},
(11)
式中,n为周跳实数解的维数.
同时,z1,z2,…,z∞满足:
(i,j=1,2,3,…,∞),
(12)
式中,Ω表示周跳为某一整数向量的所有事件空间.
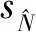
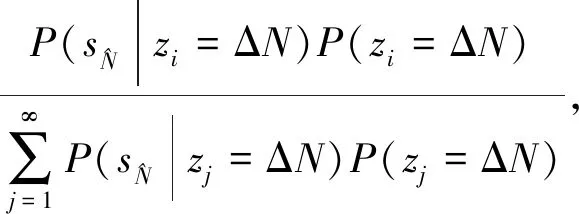
(13)
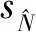
P(zi=ΔN)=P(zj=ΔN).
(14)
相应地,式(13)可写成

(15)

(16)

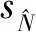

(17)
相应地,式(16)可写为

(18)
将式(17)和式(18)代入到式(15)中,可得
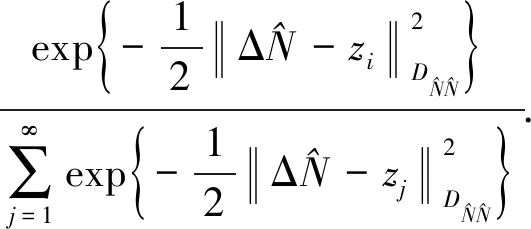
(19)

(20)
利用式(20)即可计算基于整数最小二乘所得到的周跳修复值是周跳真值的后验概率值,该值越接近于1,则所得周跳修复值的可靠性越高.
利用这个可靠性概率,还可以评价所使用的周跳探测与修复方法对该工程数据的适用性.在得到各历元周跳修复值的后验概率后,对所有后验概率值取平均,将平均值作为评价指标,即评价指标计算公式为:

(21)
式中:m为发生周跳的历元总数;pt代表第t历元周跳修复值的后验概率值.
利用式(21)得到的评价指标越大,说明该周跳探测与修复方法越适用于本工程数据的周跳探测与修复.
3 算例分析
3.1 双频周跳探测方法性能分析
本算例采用2012年3月24日,某测站采集得到的双频观测数据,卫星号为G25,采样间隔1 s,卫星截止高度角15°.分别采用多项式拟合法和TurboEdit方法对该组数据进行周跳探测与修复,并利用式(20)计算得到各历元的周跳修复值后验概率.多项式拟合法得到的L1、L2频率上的周跳修复值后验概率大小情况分别如图1(a)和(b)所示,TurboEdit法得到的周跳修复值后验概率大小如图2所示.

(a)L1频率 (b)L2频率图1 多项式拟合法后验概率情况

图2 TurboEdit法后验概率情况

表1 评价指标情况

3.2 三频周跳探测方法性能分析
本算例采用2016年6月24日,CUT0测站采集的三频观测数据,卫星号为C04,采样间隔为1 s,卫星截止高度角15°.分别采用多项式拟合法和三频无几何组合法对该组数据进行周跳探测与修复,并利用式(20)计算得到各历元的周跳修复值后验概率,多项式拟合法得到的L1、L2、L3频率上的周跳修复值后验概率大小情况分别如图3(a)、(b)和(c)所示,三频无几何组合法的后验概率大小情况如图4所示.

(a)L1频率 (b)L2频率 (c)L3频率图3 多项式拟合法后验概率情况

图4 三频无几何组合法后验概率情况


表2 评价指标情况
4 结束语
本文利用基于后验概率的周跳探测评价方法对目前常用的多项式拟合法、TurboEdit法和三频无几何组合法进行了性能分析,结果表明: 1)就双频数据而言,TurboEdit法的探测效果要优于多项式拟合法; 2)对于三频数据而言,三频无几何组合法的探测效果要优于多项式拟合法; 3)多项式拟合法适用于双频、三频观测数据,而TurboEdit法仅适用于双频观测数据、三频无几何组合法仅适用于三频观测数据,因此多项式拟合法的适用性较其他两种方法更广.
