对数变换、 导数变换的高寒草地反射光谱特征分析与识别——以那曲地区HJ-1A/HSI图像为例

刘 炜， 孙海霞， 杨晓波， 董建民

西藏光信息处理与可视化技术重点实验室， 西藏民族大学， 陕西 咸阳 712082

引 言

星载高光谱图像HJ-1A/HSI在波长范围459～956 nm内拥有115个工作波段， 平均光谱分辨率为4.32 nm。 HSI图像携带精细的光谱信息， 能够反映地物连续的波谱变化特征， 对于在大地域范围区域开展林草资源调查、 生态环境监测具有突出的应用价值[1]。 进一步对HSI图像进行一阶导数计算(导数变换)[2]， 可以去除原始光谱数据中线性及接近线性成分， 突出反映光谱反射率的增减速率， 捕捉原始光谱曲线的拐点和极值点， 从而准确定位原始光谱曲线中由于叶绿素等物质吸收形成的峰谷特征； 另一方面， 由于对数函数在定义区间(0, 1]内具有良好的放大增益， 因此还可以对HSI图像先取倒数、 再进行对数运算(对数变换)[3]。 对数变换能够更突出的反映地物谱线波形变化特征， 增强多组光谱数据之问的峰谷特征差异对比， 有利于从多谱线间的分异表现中提取敏感波段， 为准确辨识光谱特征相近的地物创造条件。

模糊C-均值(FCM)算法依据最小二乘法原理， 采用迭代法解算关于隶属度矩阵和聚类中心矩阵的目标函数， 由此得到数据集中每个样本点(即像元)到各个聚类中心的隶属度， 再依据样本点的最大隶属度值判定样本点的类别归属。 FCM是常用的图像模式识别算法， 然而， 标准FCM算法在处理高光谱图像时， 是以单个像元作为独立的数据处理单元， 其隶属度函数的计算过程没有顾及中心像元的邻域空间信息。 这导致采用标准FCM算法对高光谱图像分类后， 目标识别结果受邻域噪声影响大， 识别准确度不高， 且分类图中出现显著的“椒盐效应”[4-5]， 很难被进一步用于GIS空间分析。 为此， 设计了KICA-NFCM算法， 对标准FCM算法做出一定改进： (1)采用核独立成分分析(KICA)预先对HSI图像的多波段数据进行非线性变换， 分离出相互独立的特征波段导入分类算法。 (2)采用结合邻域加权的模糊C-均值(NFCM)分类算法。 NFCM在依据目标像元光谱特征的同时， 能够参考目标像元与邻域像元的空间关系， 并赋予邻域像元一定的权重， 使其对目标像元的识别结果产生影响。 由此降低邻域噪声对识别结果的干扰， 提升目标识别精度， 抑制“椒盐效应”。

那曲地区地处西藏自治区北部， 全区高寒干旱。 藏北嵩草、 紫花针茅、 高山蒿草和小嵩草是那曲地区具有代表性的高寒草地类型[6]。 以覆盖那曲地区那曲县、 安多县、 聂荣县的HJ-1A/HSI高光谱图像作为基础数据， 利用导数变换、 对数变换得到上述4个草种的原始光谱、 一阶导数光谱、 对数变换光谱； 通过谱线波形分异特征比较， 以及单因素方差分析和相关分析， 提取出这3种光谱数据各自适用的敏感谱段； 再设计KICA-NFCM算法利用敏感谱段从HSI图像中识别出上述4个草种， 对比3种光谱数据各自分类图的识别精度， 评价3种光谱数据敏感谱段的适用性。 并与ICA-FCM算法的分类结果比较识别精度。 本研究旨在为利用HSI图像精准开展高寒草地成像高光谱观测提供技术基础， 所用方法对于处理其他类型高光谱图像具有一定的借鉴意义。

1 数据来源与技术路线

表1显示了实验所用4景HSI图像的基本参数以及进行的5项预处理工作(波段筛选、 图像拼接、 大气校正、 几何精校正与融合)。 将图像波段95， 71， 67(中心波长依次为805， 673和656 nm)分别输入红、 绿、 蓝三通道合成标准假彩色图像， 即为图1。 为从HSI图像上采集藏北嵩草、 紫花针茅、 高山蒿草和小嵩草的光谱反射率曲线， 于2016年8月中旬， 结合Google Earth图像在那曲县开展实地踏勘， 采用近距离调查法和远观判别法为每一个草种选取样本点17个。 规定在样本点方圆30 m×30 m范围内具有相同的草种类型， 然后将样本点的经纬度坐标导入HSI图像； 之后在HSI图像上在每个样本点周围选定5个像元， 采集它们的光谱反射率曲线并计算出它们的平均值， 以此作为该样本点的光谱反射率曲线。

表1 HSI图像基本参数

图1 那曲地区HJ-1A/HSI图像

采集4种高寒草地类型的3种光谱数据： 原始光谱反射率数据、 一阶导数光谱、 对数变换光谱， 通过谱线波形分异特征比较、 以及单因素方差分析和相关分析， 提取出3种光谱数据适用的敏感谱段； 将3种光谱数据的敏感谱段分别输入KICA-NFCM算法， 自动分类识别4种高寒草地类型； 依据分类图对比3种光谱数据敏感谱段的适用性； 并与ICA-FCM算法比较分类精度。 技术路线如图2。

图2 技术路线

2 四类草种光谱特征分析

2.1 原始光谱特征分析

图3对比了在波长范围470～925 nm内， 藏北嵩草、 紫花针茅、 高山蒿草和小嵩草的光谱反射率曲线， 结果表明： (1)在波长范围505～591 nm(波段21—50)、 652～692 nm(波段66—75)、 687～782 nm(波段74—92)、 788～925 nm(波段93—112)内， 藏北嵩草的光谱曲线依次出现“绿峰”、 “红谷”、 “红边”和“近红外平台”[7]， 显现出典型的绿色植被光谱特征。 其中， “绿峰”最大值、 “红谷”最小值分别位于555 nm(波段39)、 678 nm(波段72)处， 两处光谱反射率分别为6.91%和2.69%； 在“近红外平台”788～925 nm波长范围内， 藏北嵩草的光谱反射率一直处于较高水平且平缓增加， 平均值为54.71%。 (2)与藏北嵩草相比， 小嵩草、 高山蒿草光谱曲线在“绿峰”和“红谷”处光谱反射率增高； 但在“近红外平台”范围内的反射率却降低。 在“绿峰”处， 小嵩草、 高山蒿草最大反射率依次为7.39%(552 nm)和8.51%(565 nm)， 分别是藏北嵩草的1.07倍、 1.23倍； 在“红谷”处， 二者最小反射率依次为4.45%(673 nm)和8.39%(660 nm)， 分别是藏北嵩草的2.75倍、 4.32倍； 在“近红外平台”788～925 nm波长范围内， 小嵩草、 高山蒿草的反射率平均值为39.10%和32.87%， 是藏北嵩草的71.47%和60.09%。 尤其是高山蒿草， 它在“红谷”与“近红外平台”这两处的反射率差距显著小于藏北嵩草， 致使其“红边”长度明显缩短、 倾斜幅度减小； 并且高山蒿草的光谱反射率从“绿峰”顶端至“红谷”平缓波动， 使得其在可见光范围555～692 nm内光谱曲线轮廓近似一个平台， 光谱曲线总体上表现出了退化草地的迹象。 (3)紫花针茅光谱曲线的“绿峰”、 “红谷”、 “红边”特征则进一步弱化， 其在“绿峰”565 nm处最大反射率为10.71%， 是藏北嵩草的1.55倍； “红谷”664 nm处最小反射率为11.31%， 是藏北嵩草的3.01倍； 在“近红外平台”788～925 nm内的光谱反射率的平均值为22.26%， 是藏北嵩草的42.70%。 相较于与其他3个草种， 紫花针茅在“红谷”与“近红外平台”的光谱反射率更接近， “红边”长度进一步被压缩。 光谱曲线轮廓接近于砂土地的光谱曲线轮廓， 显现出荒漠化迹象。

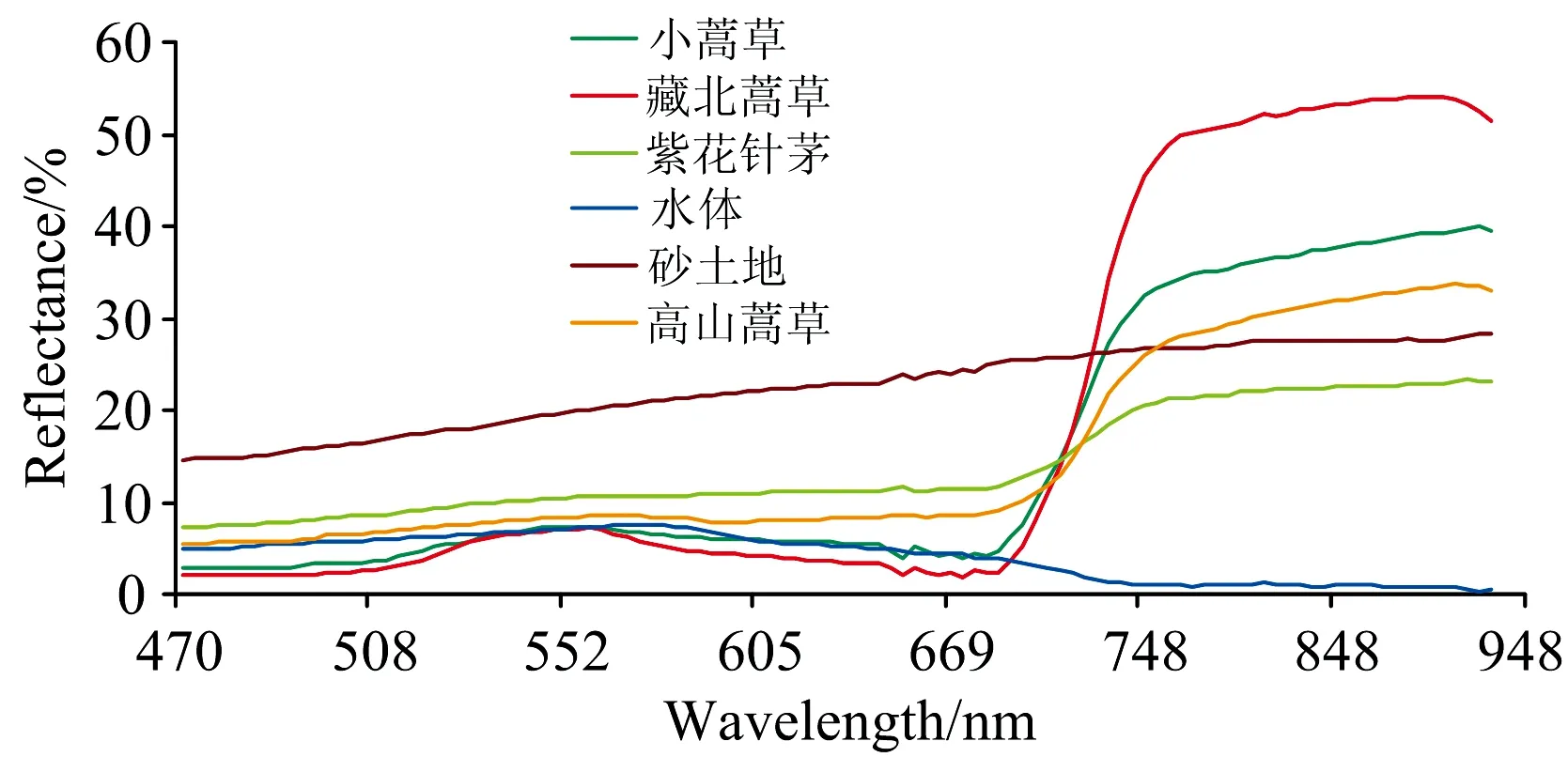
图3 四种高寒草地光谱反射率曲线图

4个草种原始光谱反射率曲线出现“绿峰”、 “红谷”、 “近红外平台”， 分别是由于草地叶片叶绿素对绿光强反射、 对红光吸收、 以及叶内细胞组织结构对近红外光反射、 折射所致。 这3个谱段是反演植被生化参量， 监测植被生长状况的敏感谱段。 依据所采集的样本点(每个草种17个点)， 将“绿峰”、 “红谷”、 “近红外平台”内各个波段的光谱反射率， 分别与4个草种(视作单因素的4个水平)进行单因素方差分析和相关分析。 结果显示在“近红外平台”范围内， 4个草种的光谱值在0.05显著水平下存在差异， 相关系数最小值为0.791， 最大值为0.828； 而“绿峰”、 “红谷”内各波段的光谱值均没有通过0.05水平的显著性检验， 它们对4个草种区分效果不及“近红外平台”内各个波段。 因此， 对于原始光谱反射率数据， 选取“近红外平台”的波长范围788～925 nm作为敏感谱段用以辨识4个草种。

2.2 一阶导数光谱特征分析

对原始反射率光谱数据进行一阶导数变换[8]， 可以去除原光谱数据中线性及接近线性成分， 突出反映光谱反射率的增减速率， 捕捉原光谱曲线的拐点和极值点， 从而有利于准确定位光谱曲线中由于叶绿素等物质吸收形成的峰谷特征。 鉴于此， 采用如式(1)对HSI图像进行导数变换

Dm(λi)=[Rm(λi)-Rm(λi-1)]/(λi-λi-1)

(1)

式(1)中，i为HSI图像波段序号， 取值范围为6～112；λi表示第i波段的波长位置；m=1～4， 分别代表藏北嵩草、 紫花针茅、 高山蒿草和小嵩草这4个草种。Rm(λi)表示第m种草地类型， 在波长位置λinm处的原始光谱反射率；D(λi)则表示第m个草种， 在表示波长位置λinm处的一阶导数光谱值。

图4 四种高寒草地一阶导数光谱曲线图

图4对比了在“红边”687～782 nm波长范围(波段74—92)内， 藏北嵩草、 紫花针茅、 高山蒿草和小嵩草的一阶导数光谱曲线， 结果表明： (1)在“红边”范围内， 4个草种的一阶导数光谱均呈现出“凸”状特征峰， 但特征峰形态差异明显。 其中， 藏北蒿草具有典型的“双峰”特征， 其“次峰”、 “主峰”分别位于701 nm(波段77)、 737 nm(波段84)； 小嵩草、 高山嵩草、 紫花针茅的“次峰”/“主峰”则分别位于701 nm(波段77)/732 nm(波段83)、 711 nm(波段79)/726 nm(波段82)、 721 nm(波段81)/732 nm(波段83)。 相较于其他3个草种， 在紫花针茅“凸”状特征峰顶部， 主、 次峰之间的波长距离最小， 主、 次峰的振幅差值也最小， “次峰”特征被弱化。 (2)在绿色植被“红边”特征中， 一阶导数光谱曲线的“红边位置”、 “红边振幅”、 “红边面积”被认为是用来跟踪叶绿素、 生物量和物侯变化的最具显著性的3个诊断性指标[9]。 高山蒿草、 小嵩草、 藏北嵩草的“红边位置”分别位于726， 732和737 nm， 依次向长波方向移动； 藏北嵩草、 紫花针茅、 高山蒿草和小嵩草的“红边振幅”分别为62.61， 33.06， 24.92和10.14。 其中， 紫花针茅的“红边振幅”最小， 分别是藏北嵩草的16.20%、 小嵩草的30.67%和高山蒿草的40.69%； 另外， 通过数值积分可以得到藏北蒿草、 小嵩草、 高山嵩草和紫花针茅的“红边面积”分别为518.703， 305.241， 198.322， 98.171。 藏北蒿草的“红边面积”分别是小嵩草、 高山蒿草和紫花针茅的1.70倍、 2.62倍和5.28倍。 显然， 相较于其他3个草种， 紫花针茅的“红边”特征表现最弱， 显示出其生长旺盛程度不及其他3个草种； 而藏北蒿草则显现出旺盛的生长状况。

“红边位置”能够捕捉到原始光谱反射率增长速度由快到慢变化转折的“拐点”， 常被用作分析植被生长状况、 跟踪植被营养亏缺程度的重要指标。 图4表明在“红边位置”附近， 4个草种原始光谱反射率增速存在明显差异。 依据所采集的样本点， 将“红边位置”两侧687～782 nm范围内的一阶导数光谱值， 分别与4个草种(作为单因素的4个水平)进行单因素方差分析和相关分析。 结果表明， 只有在波长范围711 nm(波段79)～742 nm(波段85)内， 4个草种的一阶导数光谱值在0.05水平下存在显著差异； 相关系数最小值、 最大值分别为0.783和0.812。 因此， 对于一阶导数光谱数据， 可以选取“红边位置”两侧波长范围711～742 nm， 作为敏感亲段用以辨识4个草种。

2.3 对数变换光谱特征分析

对数函数在定义区间(0, 1]内具有良好的放大增益。 通过对植被原始光谱反射率数据先取倒数、 然后再进行对数运算(对数变换)， 可以突出表现谱线波形变化特征， 增强多组光谱数据之问的峰谷特征差异， 从而有利于从多谱线间的分异表现中提取敏感波段， 改善对光谱特征相近地物的识别精度。 鉴于此， 采用如式(2)对HSI图像进行对数变换

RLm(λi)={ln[Rm(λi+1)]-1}3

(2)

式(2)中，i，λi，m，Rm(λi)的意义同式(1)。RLm(λi)表示第m个草种， 在波长位置λinm处的对数变换光谱值。

图5 四种高寒草地对数变换光谱曲线图

图5对比了波长范围472～925 nm内， 藏北嵩草、 小嵩草、 高山蒿草和紫花针茅的对数变换光谱曲线， 结果表明： (1)在505～591 nm(波段21—50)范围内， 4个草种对数光谱值均呈现先下降、 后上升的“凹”状波谷。 在“凹”状波谷中部， 藏北嵩草、 小嵩草、 高山蒿草、 紫花针茅对数光谱出现最小值， 依次为-60.37(555 nm)， -64.04(552 nm)， -29.60(565 nm)和-106.75(565 nm)。 相较之图3中的“绿峰”， 在图5所示“凹”状波谷的中部， 4个草种谱线之间的距离有所增加， 但仍容易混淆藏北嵩草与小蒿草的谱线。 (2)在652～692 nm(波段66—75)范围内， 藏北嵩草、 小嵩草、 高山蒿草、 紫花针茅对数光谱的最大值依次为-1.64(678 nm)， -18.83(673 nm)， -42.01(660 nm)和-111.69(664 nm)。 与图3中的“红谷”比较， 在652～692 nm范围内， 4种草地谱线之间的距离显著增加， 能够被准确分辨。 (3)在687～925 nm(波段74—112)范围内， 4个草种对数变换光谱值均呈现出先快速下降、 再小幅波动延伸的变化趋势。 其中， 在788～925 nm(波段93—112)内， 藏北嵩草、 小嵩草、 高山蒿草、 紫花针茅对数变换光谱值变化稳定， 其平均值依次为： -499.58， -381.27， -329.82和-240.87， 与图3中的“近红外平台”比较， 在图5中788～925 nm内各谱线之间相互距离明显增加， 因而分异表现更为显著。

依据所采集的样本点， 将505～591 nm(波段21—50)、 652～692 nm(波段66—75)、 788～925 nm (波段93—112)内的对数变换光谱值， 分别与4个草种(视作单因素的4个水平)进行单因素方差分析和相关分析。 结果显示， 在波长范围669～682 nm(波段70—73)、 788～925 nm(波段93—112)内， 4个草种的一阶导数光谱值在0.05显著水平下存在差异； 相关系数最小值、 最大值分别为0.795和0.837。 因此， 对于对数变换光谱数据， 可以选取两个波长范围669～682和788～925 nm， 作为敏感谱段用以辨识4个草种。

3 KICA-NFCM算法

3.1 KICA非线性变换

高光谱图像每个像元在各波段的灰度值(即观测信号的各个分量)由该像元覆盖的多种地物的光谱特征(即源信号的各个分量)混合而成， 源信号各分量之间彼此独立。 独立成分分析(ICA)是一种线性变换， ICA基于高阶统计矩分析观测信号， 能够从观测信号中提取出相互统计独立且呈非高斯分布的源信号估计值。 HSI图像光谱分辨率高， 相邻多波段之间存在高相关性和高冗余度。 利用ICA线性变换， 可以将HSI图像各波段转换成光谱信息相互独立的分量， 去除相关性对图像分类的不利影响。 然而， 囿于100 m的空间分辨率， 一个HSI图像像元通常覆盖相互独立的多种地物。 受太阳光照射角度、 地形高程差异等因素的影响， 这个HSI像元在每个波段的灰度值(观测信号的一个分量)实则为其覆盖的多种地物的光谱特征(源信号各个分量)的非线性组合。 因此， 直接利用ICA线性变换处理HSI图像就存在一定的局限性。

采用核独立成分分析(KICA)方法对HSI图像进行预处理。 KICA先以满足Mercer条件的对称函数作为核函数K(xi,xj)， 代替两向量间的内积运算(ICA是以内积运算表达源信号各分量之间的线性组合)， 实现对多波段数据的非线性变换， 将其映射到高维希尔伯特空间， 使其线性可分； 然后再在高维空间中对被映射的数据进行ICA分析。 KICA改善了ICA处理非线性问题时的缺陷， 能够从高光谱图像中有效分离出增强目标和背景光谱特征差异的独立信源， 凸显出在原低维光谱空间没有表现出的特征， 支持后续图像通过聚类分析准确识别4个草种。 KICA算法的应用描述如下：

(1) 设单波段HSI图像有M行N列个像元， 将具有H个波段的HSI图像的按波段序号展开为H行(M×N)列的矩阵X，X即为观察信号。

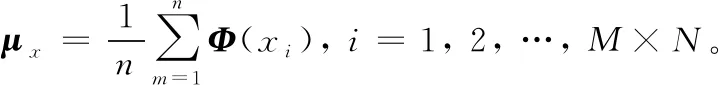
(4) 采用FastICA算法分析(Φ(xi))′,i=1, 2, …n， 计算出解混矩阵WΦ， 得到源信号的估计值yΦ。

3.2 NFCM分类

由于FCM算法是以单个样本点作为数据处理单元， 它忽略了样本点的空间邻域信息， 导致算法对孤立点敏感， 抗噪性能差， 以致在对HSI图像聚类分析后， 生成的地物图斑散碎， 同质区域在拓扑空间上连通性低。 实际上， 在那曲地区， 城区以外地表上各种地物通常连续分布， 反映到HSI图像上， 相邻像元同属一个类别的概率大， 因此在对HSI图像聚类分析时， 不但要考虑目标像元的光谱特征， 而且还应考虑该像元与邻域像元的空间关系， 赋予邻域像元一定的权重， 使其对中心像元的识别结果产生一定影响。 由此降低HSI图像的光谱噪声对孤立点识别结果的影响， 改善同质区域的连通性， 得到更为连续、 完整的地物分类图斑。 鉴于此， 设计了结合邻域加权的模糊C-均值 (NFCM)算法， 对传统FCM算法做出一定改进。

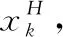
设第H号波段图像f为M行N列，fH(i,j)为坐标(i,j)处的图像像元的灰度值， 1≤i≤M, 1≤j≤N。 定义一个窗口半径为r的方形邻域窗口E={e(i+a,j+b)|a,b∈[-r,r]}(即窗口尺寸为(2r+1)×(2r+1))， 其中e(i+a,j+b)是邻域内各个像元的权重系数， 反映了像元(i+a,j+b)对中心像元(i,j)的影响力

e(i+a,j+b)=

a,b∈[-r,r]∧(a,b)≠(0, 0)

(3)

(4)

4 三种高光谱数据和2种算法应用对比

按图2所示技术路线从4个草种的原始光谱、 一阶导数光谱、 对数变换光谱中提取各自适用的敏感谱段(表2)； 然后将上述3种光谱数据的敏感谱段分别导入KICA进行非线性变换， 之后对KICA各个输出特征计算方差， 并按方差值大小对KICA所有输出特征进行排序。 设定累积方差百分比贡献率阈值为95%， 选取达到该阈值时排序在前的KICA输出特征； 将3种光谱数据各自的优选特征分别导入至NFCM， 并设置初始条件(模糊隶属度加权指数m=2.0， 加权控制参数θ=4)， 和迭代收敛条件(隶属度最小变化量为ε=1×10-6， 允许最大迭代次数为Tmax=200， 窗口半径为r=1)。 KICA-NFCM算法对上述3种光谱数据图像进行分类， 结果如图6(a)—(c)。

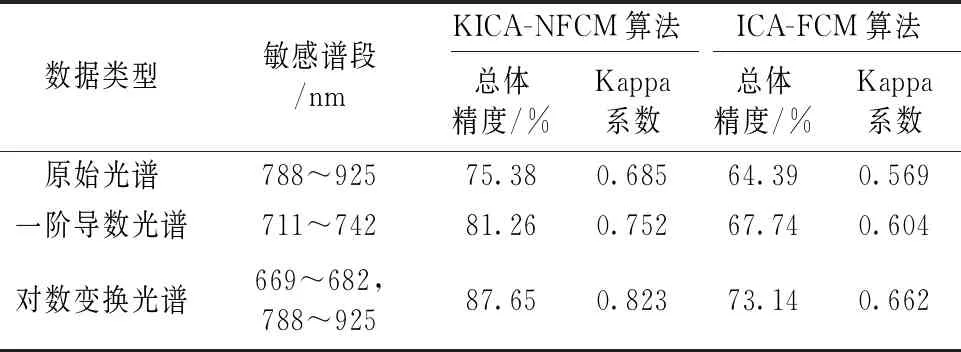
表2 分类精度比较

图6 三种光谱数据KICA-NFCM算法分类

为与KICA-NFCM算法比较， 还将3种光谱数据敏感谱段内的各波段, 直接导入结合ICA与标准FCM的算法， 分类结果如图7(a)—(c)。 在图像分类后， 从原HSI图像中随机抽取426个像元， 从图像元目视判别类别归属， 再与图6(a)—(c)， 图7(a)—(c)所示分类结果依次进行比较， 然后据此计算每个分类图的混淆矩阵以及总体精度、 Kappa系数(表2)。

图7 三种光谱数据ICA-FCM算法分类

对比图6(a)—(c)、 图7(a)—(c)表明： 采用“对数变换光谱/KICA-NFCM算法”组合能够最准确的识别出4个草种[图6(c)]， 图6(c)的总体精度、 Kappa系数分别为87.65%， 0.823， 较之图6(a)分别提高18.31%， 20.15%； 较图6(b)分别提高7.86%， 9.44%， 并且在图6(c)中， 4个草种的图斑轮廓位置准确， 可与原HSI图像准确叠加复合； 叠加对比图6(a)—(c)进行目视检查还可以发现， 在图6(a)和(b)中， 混分藏北嵩草与小蒿草、 在水体图斑边界处将水体图斑误分为藏北嵩草、 将高山蒿草误分为小嵩草或紫花针茅、 将紫花针茅误分为砂土地的情况主要出现在不同草种相互邻接的地带， 而在图6(c)的相同地域， 上述遗漏、 错误判别小斑类别的情况显著减少。 另一方面， 叠加对比图6(a)—(c)和图7(a)—(c)进行目视检查发现， 在图7(a)—(c)中分类图斑内部分布有孤立的噪声碎斑， 图像“椒盐效应”显著， 部分砂土地图斑轮廓线杂乱， 发生了位置偏移。 而在图6(a)—(c)中， 同质区域的连通性得到改善， “椒盐效应”被抑制， 为进一步执行GIS分析创造条件。

5 结 论

对数函数在定义区间(0, 1]内具有良好的放大增益， 通过对4个草种原始光谱反射率数据进行对数变换， 可有效增强多组相似光谱数据之问的峰谷特征差异， 有利于通过谱线波形分异特征比较提取敏感谱段辨识4个草种； 较之ICA-FCM算法， KICA-NFCM算法能够提高从HSI图像上识别4个草种的准确度， 并有效去除分类图中的噪声碎斑， 抑制“椒盐效应”。 2018年4月、 5月， 我国陆续发射了珠海一号星座群4颗高光谱卫星、 以及高分5号高光谱卫星[10]。 在后续研究中， 研究团队将协同使用上述高光谱卫星数据与HSI图像， 在更大尺度的地域范围内， 测试、 改进本文提出的“对数变换光谱/KICA-NFCM算法”， 为在那曲地区开展高寒草地成像高光谱观测提供技术支持。

致谢: 感谢中国资源卫星应用中心提供HJ-1A/HSI和HJ-1A/CCD数据。