基于Copula函数的热轧支持辊健康状态预测模型

李天伦，何安瑞，邵 健✉，付文鹏，强 毅，谢向群

1) 北京科技大学工程技术研究院，北京 100083 2) 上海梅山钢铁股份有限公司热轧厂，南京 210039 3) 机械科学研究总院，北京 100044

支持辊作为热轧机的重要损耗备件，因其制造周期长、服役周期长、使用成本高、异常失效后损失大等特点，在各大钢厂属重点管理产品[1].支持辊的工作环境非常恶劣，在热轧过程中，轧辊磨损和热凸度使其在长期服役中出现轴向不均匀磨损，磨损导致的辊形变化使辊间接触压力的分布随之变化，进而改变承载辊缝的形状，对带钢的板形及其控制性能造成影响[2].当支持辊磨损程度较为严重，即板形控制能力无法满足下游产线要求时，需要对支持辊进行更换.目前各大钢厂多按照轧制吨位数确定其维护时机，例如文献[3]指出支持辊F1～F6机架的换辊周期为20万吨、F7机架的换辊周期为10万吨；文献[4]提出了F1～F4机架每15万吨、F5～F7机架每7万吨更换支持辊的维护制度.不同产线间换辊制度的差异一般与其轧辊材质、产品结构、工艺制度等有关.上述换辊模式属于典型的定期维护，容易存在设备的不及时维护或过度维护，对热轧最终产品的板形质量造成影响，同时增加了企业的生产成本.

由于轧制过程中支持辊的磨损机理复杂，不同品种的带钢在热轧过程中对其影响也不尽相同，难以直观发现支持辊的失效或故障状态并对其表征.此外，支持辊的换辊周期较长，剔除异常数据后并不能获得足够的样本数据集，也对支持辊健康状态的预测造成了一定困难.为了实现复杂工业系统从状态监控到健康管理的转变，美国军方最先提出了故障预测与健康管理技术（Prognostics and health management，PHM），使其节省了30%的维修费用[5−6].我国在军工、航天等领域也进行了PHM技术的应用探索[7−9].工程应用方面，依据机理模型从振动信号中分析发现故障特征的方法在轴承[10−12]、行星齿轮箱[13−14]等旋转机械设备的故障诊断中取得了良好的效果.近年来随着信息技术的发展，基于数据驱动的寿命预测方法逐渐成为研究热点并取得了一定成果.人工神经网络[15−16]、支持向量机[17−19]、贝叶斯回归模型[20−21]、相似性[22]等方法在PHM领域均取得了一些成果，但从文献中可以看出，目前研究重点在于如何通过算法实现高精度寿命预测，所用的数据源通常比较理想、规整，较少考虑到设备所处的外部环境特点，特别是输入的不确定性、多维度、少样本对预测结果的影响.本文使用数据驱动建模的方法，依据轧制周期中弯窜辊工艺的使用特性建立参数表征支持辊健康状态，之后考虑轧制过程的复杂性对工况进行聚类划分，再在各工况下对支持辊健康状态进行基于Copula函数的数据建模并融合预测结果，达到对复杂工况下支持辊健康状态预测的目的，最后使用某钢厂1780热连轧产线支持辊数据进行实验验证.

1 支持辊健康状态建模

1.1 VHI的构建方法

在热轧过程中，没有信号能够直接反应支持辊的健康损耗，可考虑使用多个数据信号组合传递信息来表征支持辊的寿命退化特征，即虚拟健康指数（Virtual health index，VHI）.随着涡流、超声、磁粉等无损探伤手段在轧辊下机检测中得到普及应用，由轧辊疲劳或裂纹累计导致的轧辊剥落、爆辊等失效事故有效减少[23]，目前热轧环节的支持辊换辊时机主要由板形质量决定，因此考虑从轧机对板形的控制能力角度间接构建VHI.通常，热轧机的板形调控手段主要有弯辊、窜辊两种，支持辊使用后期二者均处于极限位置的概率增大，甚至长期保持在极限位置，导致板形控制能力丧失.综合生产过程中弯窜辊的数值变化构建轧机支持辊的VHI，以此表征带钢板形的剩余控制能力，即可描述支持辊的健康状态.

以某1780热连轧产线为案例，F1～F7机架工作辊均使用连续可变凸度（Continuous variable crown，CVC）辊形.设轧辊轴向窜动的行程范围s∈[−sm,sm]，及相应的辊缝凸度范围Cw∈[C1,C2]，则利用辊缝凸度与轧辊轴向窜动量的线性关系，可求得任意窜辊量的辊缝凸度：

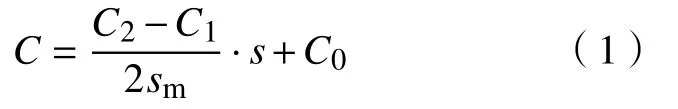
式中，C0为不窜辊即s=0时的辊缝凸度.

通过二维变厚度有限元方法离线计算，然后经多元非线性回归得到的承载辊缝及弯辊力系数计算模型的表达式如下[24]：

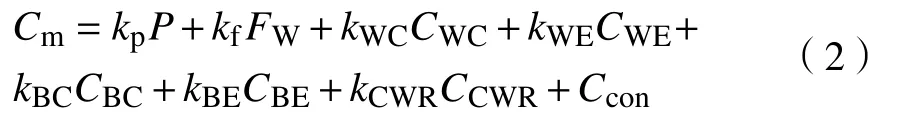
式中，kp为轧制力影响系数；P为轧制力设定值；kf为弯辊力影响系数；FW为弯辊力设定值；kWC为工作辊中部辊形影响系数；CWC为工作辊中部辊形特征值；kWE为工作辊边部辊形影响系数；CWE为工作辊边部辊形特征值；kBC为支持辊中部辊形影响系数；CBC为支持辊中部辊形特征值；kBE为支持辊边部辊形影响系数；CBE为支持辊边部辊形特征值；kCWR为工作辊初始辊形影响系数；CCWR为工作辊初始辊形特征值；Ccon为常数项，其值与机架间凸度分配策略及自学习有关.其中弯辊力与工作辊辊形对板形机械凸度的影响互为可逆，即存在成对出现的FW、CCWR数值，保持式中其他系数不变，则可以求得单位弯辊力与窜辊数值的换算关系为：

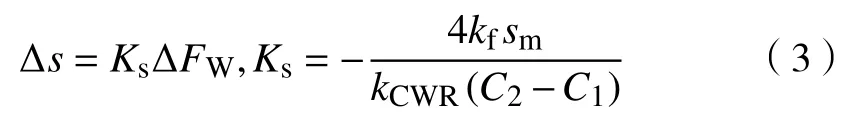
式中：∆FW为工作辊为调整板形所增加的弯辊力数值，kN；∆s为由工作辊弯辊值变化对应换算的等效窜辊值，mm.将弯窜辊的作用综合在一起，即可使用一个变量描述支持辊的健康状态，即VHI，如式（4）所示：

式中：SRBF和SRSH分别为弯辊和窜辊对板形的作用值；dRBF0和dRBF分别为弯辊力的平衡值与实际值，kN；SRSH为窜辊值，mm；[K(dRBF0−dRBF)]为弯辊力偏移量的等效窜辊.理论初始状态下设定弯辊力为dRBF0，窜辊处于−Sm的极限位置，代入公式VHI=0，随着轧制计划的推进工作辊逐渐正窜，VHI数值随之增长；当设定弯辊力dRBF0，窜辊处于Sm极限位置时辊系的控制能力到达极限，不能继续对板形进行有效调控，此时VHI=1，定义为支持辊理论失效点.实际生产中由于设定弯辊力过大或过小，极限状态下会使VHI的数值超出理论范围，此时取理论上下限值处理，转化后的VHI范围区间为[0,1]，适合用于支持辊健康状态的表征.

在实际生产中，更换支持辊对生产效率影响较大，考虑和上下游检修的生产匹配，支持辊的更换通常以批量更换为主，一般当F7机架支持辊失效时则更换全部机架或下游F5～F7机架的支持辊，因此上述处理方法计算产生的F7机架VHI可以较为准确的描述支持辊生命周期内的退化特征，满足后续预测模型的要求.

使用某钢厂1780热连轧产线的支持辊数据，在连续8个月的时间内收集到F7机架有效数据5组，具体情况如表1所示，按照4组训练集1组测试集的比例划分数据，进行交叉验证完成建模过程.将支持辊完整轧制单元的弯窜辊数据带入公式计算，由于F7机架对带钢热轧出口板形起决定性作用，其VHI数据表现出明显的随轧制计划推进而上升的带状分布趋势（以1#数据为例），如图1所示.

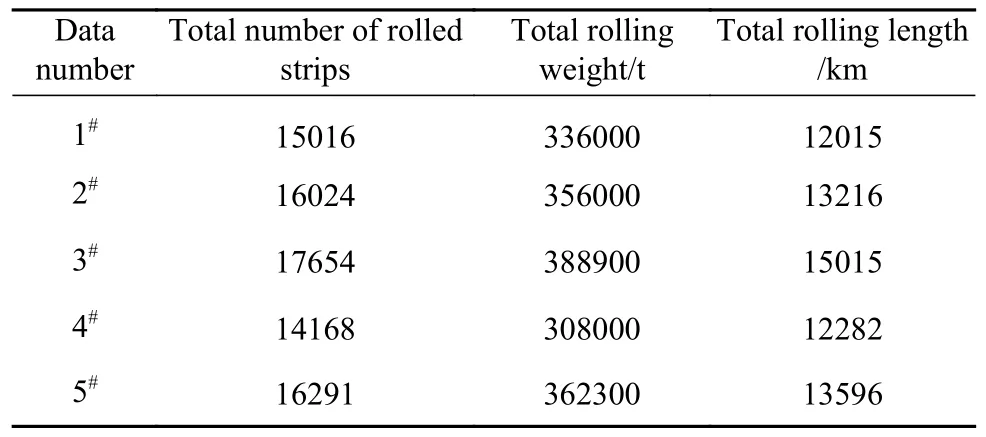
表1 某钢厂1780热连轧产线F7机架支持辊使用情况统计Table 1 Statistics on the use of F7 back-up roll in a 1780 hot rolling line

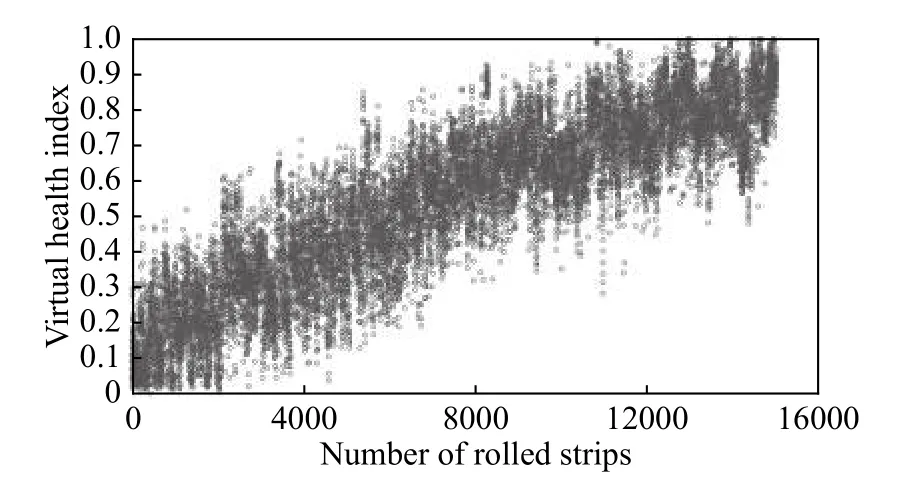
图1 F7机架VHI数据（1#）表现出随轧制计划推进而上升的趋势Fig.1 Rising trend of F7 stand VHI data (1#) with the rolling schedule

1.2 VHI带状分布区间工况剥离

图1所构建的VHI数据虽然具有单调趋势，但其上升趋势呈带状分布且范围宽泛，若将该数据直接用于后续预测步骤，数据的不确定性会对最终的预测结果带来较大误差.轧制过程中弯窜辊的设定值主要受带钢规格及变形抗力等因素影响，VHI数据的带状分布也由二者的差异导致.因此，使用K-means聚类方法对VHI数据进行预处理，选择带钢的变形抗力和宽厚比两维数据作为聚类算法的输入，将带钢按照变形抗力大小分为3个不同强度类别，按照带钢厚度差异分为3个不同规格类别，即在变形抗力、宽厚比两个维度上的数据各分为3档，由此确定聚类数为9.对轧制条件不同的数据划分不同的工况，在不损失数据信息的情况下降低数据噪音.

K-means聚类的运算结果如图2所示，其中横坐标为带钢变形抗力，纵坐标为宽厚比.将聚类结果中的每一个簇视作一种工况，据此对F7机架的原始VHI数据进行拆分，得到某轧制计划内单一工况下的支持辊健康状态衰减趋势，以1#数据−工况1为例，该工况代表变形抗力较大而宽厚比处于较低档位的带钢样本，如图3所示.可见工况剥离后VHI数据的带状区间宽度从0.5下降至0.3左右，集中效果明显，由于轧辊磨损对轧制过程中弯窜辊的设定值也有影响，带状区间无法完全消除.

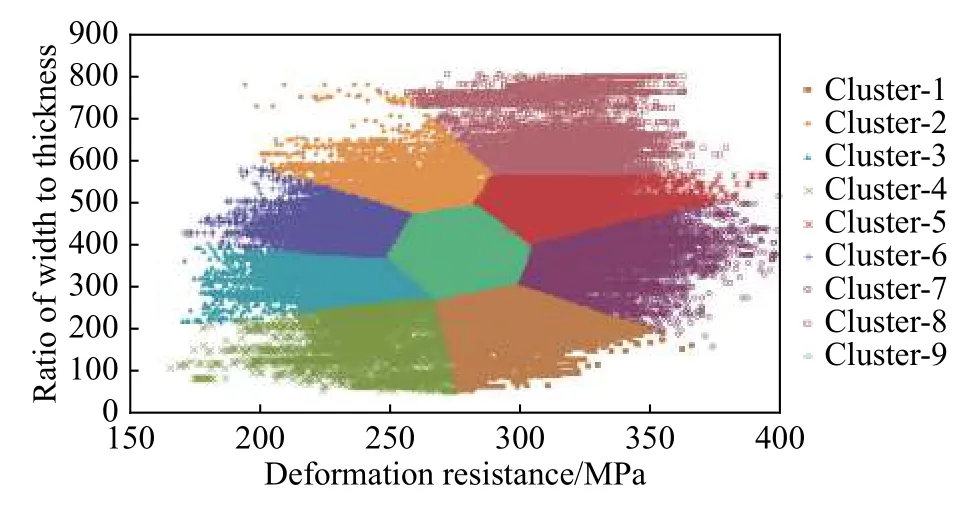
图2 K-means聚类结果示意图Fig.2 K-means clustering results

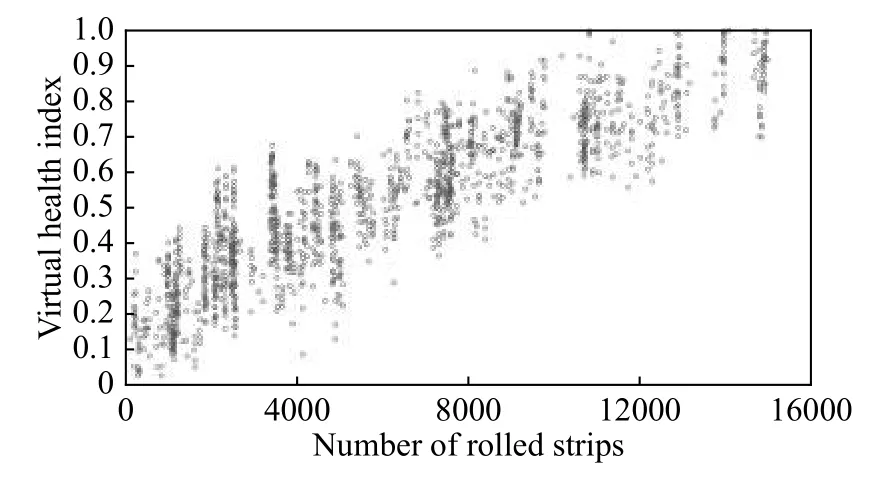
图3 原始数据统一聚类后1#数据−工况1效果图Fig.3 Working condition 1 of 1# data after clustering

支持辊的VHI应是单调递增的，虽然对F7机架的VHI数据进行了工况剥离处理，但仍存在较大的数据波动，因此需要对各工况的VHI数据进行降噪和单调处理，使其满足支持辊健康状态单调的物理意义，以便顺利进行算法后续步骤.实际情况下支持辊的磨损情况会随轧制计划的推进逐渐劣化，支持辊磨损的累积以及磨损不均使其健康状态的衰减速率逐渐增加，因此选用指数函数y=keax的形式对VHI数据进行拟合，得到的单工况理想化训练集VHI曲线如图4所示（以工况1为例）.

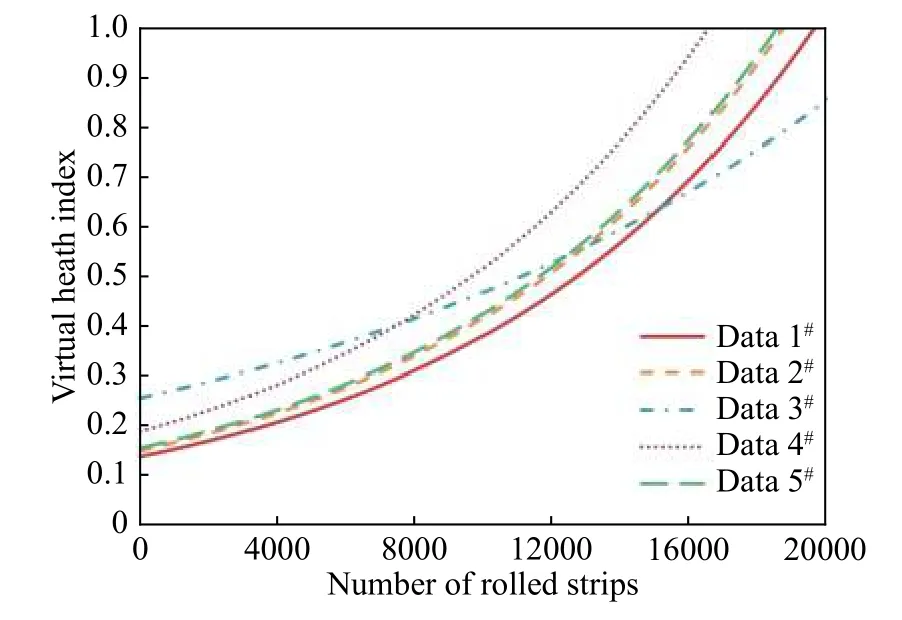
图4 工况1支持辊VHI数据拟合降噪后结果示意图Fig.4 Result of noise reduction after fitting VHI data of working condition 1

2 基于Copula函数的数据建模方法

大多数据驱动的预测方法均需要基于某些函数关系的假设，例如回归方法中函数表达式的结构，神经网络中节点数与激活函数的设置等.支持辊寿命预测问题中数据高维、不确定性等特点使得算法难以找到合适的函数关系，加之支持辊服役周期较长，难以获得大量的运行−失效数据，为支持辊健康状态的准确预测带来了困难.将Copula函数的性质运用于数据预测中，可以建立数据集在不同时刻间的分布关系，消除了剩余使用寿命与表征信号之间函数关系的假设，建立一个通用的统计关系取而代之，同时统计模型可以按照分布规律产生大量数据样本，使得预测算法只由可用的训练数据集驱动.

2.1 Copula函数在数据预测中的应用

Copula函数描述变量间的相关性，其理论核心为Sklar定理，可以表述为[25]：F(x1,x2,...,xn)=C(F1(x1),F2(x2),...,Fn(xn))，其中F1(x1),F2(x2),...,Fn(xn)为分散的n个边缘分布函数，使用某一类型的Copula函数C(u1,u2,...,un)连接形成他们的联合分布函数F(x1,x2,...,xn).若将某变量不同时刻数值的分布看作边缘分布，通过Copula函数的连接则可以研究某变量在时间序列上不同时刻间的联系与变化关系，利用这一特性即可将Copula函数运用到数据预测中.此外，由于Copula函数是以概率分布的形式描述边缘分布之间的关系，只要能够求得预测数据的分布情况即可使用Copula预测方法完成预测，可见基于Copula函数的预测方法可以满足对于预测结果的概率分布输出要求，且对数据集体量的需求较小，比较适合用于少样本下的寿命预测.

2.2 使用Copula函数进行预测的建模步骤

基于Copula函数的健康状态预测需要在已知某时刻真实健康状态分布的情况下来确定之后可能达到失效状态的时间点.在支持辊健康状态预测的研究中，需要将VHI指数离散成一定数量的退化等级，之后建立某一等级Tn与最终失效等级Tend支持辊健康状态之间的相关关系.其建模过程如图5所示，具体实施步骤在下一章以实例形式给出.

3 单工况Copula模型的建立过程

3.1 VHI曲线的离散化处理

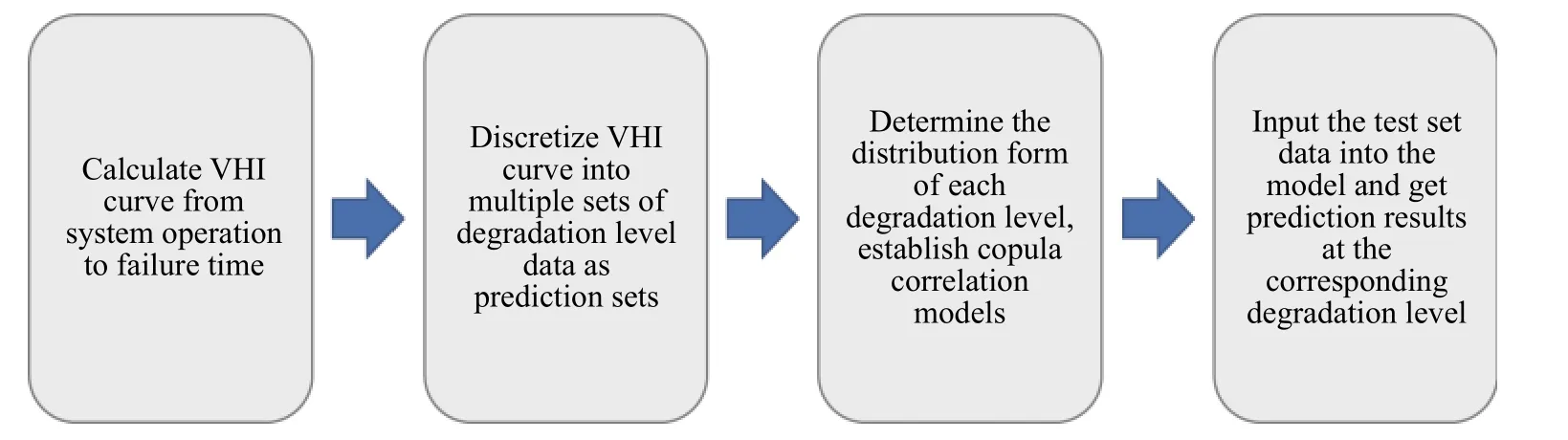
图5 使用Copula函数预测支持辊健康状态的建模流程图Fig.5 Flow chart for predicting the health of back-up roll using Copula function

一个测试单元的支持辊VHI会在不同时刻表现出不同的健康状态，在已知工况数据下按一定间隔确定若干时刻，划分为退化等级Ti，其中i的范围从1到j，j为模型划分的退化等级数量，即可描述支持辊在不同时刻下VHI的分布情况.本研究将各工况测试数据集中VHI的最小值作为建模起点，以支持辊失效标志即VHI值达到1时作为建模终点，在建模区间内等距划分50个健康状态退化等级，每个退化等级Ti分别与失效退化等级T50建立联合分布模型，得到50组不同类型Copula函数构成的Ti−T50数据模型，每个模型中均包含4组训练集数据及按Copula函数分布得到的补充数据，退化等级的划分示意图如图6所示.其中左侧表示数据集VHI值分别到达退化等级Ti，T50时的轧制块数值，到达Ti的轧制块数记为ti−1,ti−2,ti−3,ti−4，到达T50的轧制块数记为t50−1,t50−2,t50−3,t50−4，纵坐标均为退化等级对应的VHI值，右侧四个圆圈为训练集数据点，大面积实点为由Copula模型计算扩充而来的训练数据集；横坐标为数据点在Ti等级时已经轧制的块数值，纵坐标为其在T50等级时轧制达到的块数值.

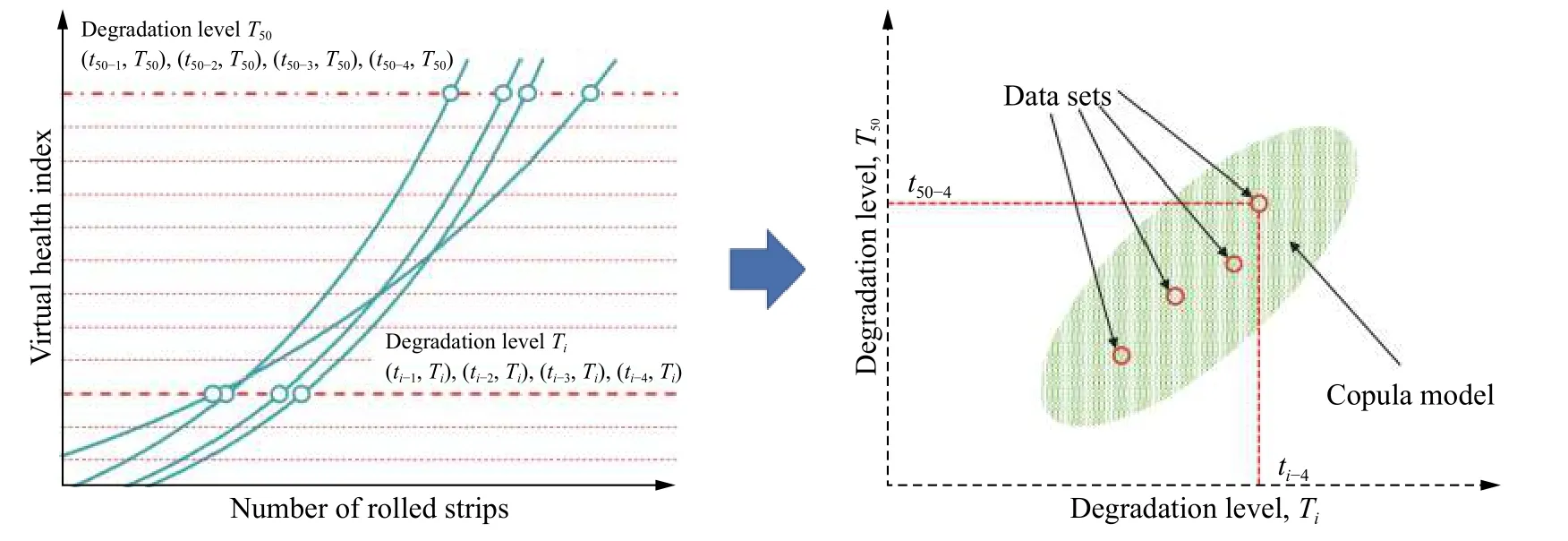
图6 对单工况训练集数据划分退化等级示意图Fig.6 Data degradation level for single-working-condition training set

3.2 最佳Copula函数类型的确定

在利用Copula理论对多元分布函数进行建模时，不同类型的Copula函数有着各自的适用范围，一般可以通过联合分布数据集与各类Copula函数的分布形式对比来匹配合适的参数.但对于数据量稀少的情况，无法通过观察得到准确的联合分布形式，使用极大似然估计方法在Gumbel、Frank、Clayton 3种常见类型中选择确定各个Tn−T50数据模型匹配的Copula函数类型.

对于本文案例使用的数据，需要将某一时刻Tn与 失效等级T50间的支持辊轧制块数进行Copula建模，认为各失效等级下的数据均符合正态分布，考虑联合分布函数C和各变量边缘分布Fn都是连续的情形，其似然函数可以写作：

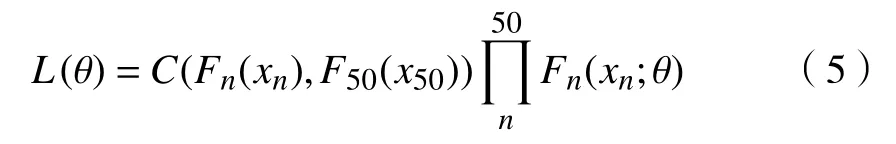
将某时刻支持辊达到轧制块数的概率分布u与 最终时刻支持辊达到轧制块数的概率分布v带入到3种不同Copula函数的概率密度函数中，利用极大似然方法分别求得每种Copula函数对应的最大似然估计值，之后得以选出三者中最优的Copula类型用作当前时刻的退化等级建模.图7为3种不同类型函数扩充得到的Copula模型典型样本，可见扩充数据的分布形式（头部发散、两端发散、尾部发散）差别明显，随退化等级的推进数据分布逐渐收敛，说明使用极大似然估计确定最优Copula类型的方法是可行的.

3.3 提高模型适应性的平移处理

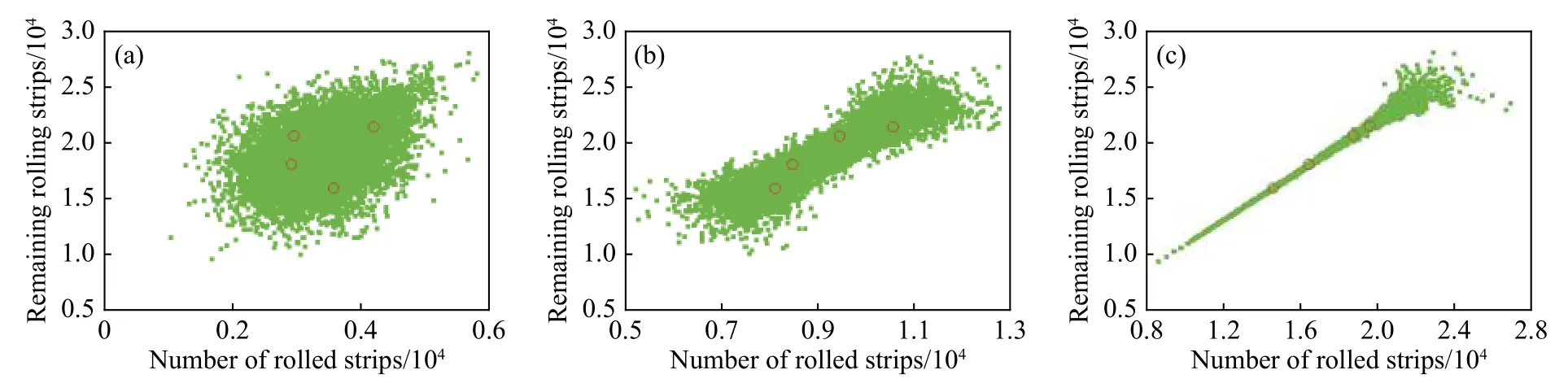
图7 处于不同退化等级下的分布模型适用于不同类型的Copula函数描述.（a）T12-T50, Gumbel; （b） T26-T50, Frank; （c） T46-T50, ClaytonFig.7 Distribution models at different degradation levels fit for different types of Copula function descriptions: (a) T12-T50, Gumbel; (b) T26-T50, Frank;(c) T46-T50, Clayton

由于退化等级的划分层数有限，加之训练集数据量不足，某些退化等级对应的Copula相关性模型可能无法完全代表特定时间内测试集数据样本的分布形式.发生这种情况时，测试数据集可能达到某一退化等级的时刻过早（模型数据集左侧）或过晚（模型数据集右侧），如图8（a）所示，导致式（5）计算条件概率密度函数时无法取到对应的数值.

这一问题可以将Copula模型进行变换得以解决，如图8（b）所示.若测试集相对于训练集数据更早到达退化等级，将Copula模型的中心向左平移，这样就可以利用Copula相关性模型得到测试集达到该等级剩余健康寿命的条件概率密度函数.然而为了获得等效的条件概率密度函数，若由于测试集到达退化等级的时间与训练集差别较大，求得的失效时间应该相应的进行增（对应模型向右平移）减（对应模型向左平移），作为退化速率的补偿.

3.4 预测结果的获取

对热轧支持辊的健康状态进行预测时，预测曲线会经过若干个退化等级，每个退化等级对应的Ti−T50模型均会给出支持辊最终失效时间的预测区间与概率分布，最终的预测结果需要结合每个模型给出.理论上如果VHI达到所有退化等级Ti,...,Tj的概率密度函数均是可用的，那么就可以使用Copula函数将VHI先后到达任意两个退化等级Ti和TN(N＞i)的二元概率密度函数构建出来，使用式（6）可以近似支持辊最终失效时间T50的条件概率密度函数.其中β为归一化参数，使得概率密度函数在整个域上的积分等于1.

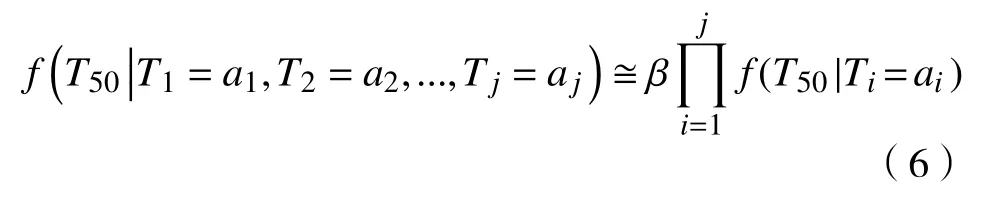
单工况Copula模型的预测结果如图9所示，其中横坐标表示支持辊已轧块数，纵坐标为预测得到的支持辊在当前工况健康状态下的剩余可轧块数，阴影部分代表预测值的置信区间，阴影中间的实线为预测点对应的预测值.

4 复杂工况下预测结果的融合

4.1 单工况预测结果的转化

单工况数据集在完成Copula预测前后，描述支持辊健康状态的尺度发生了改变.Copula模型的原始输入为VHI随轧制块数的变化关系，如图4所示；而Copula最终输出的是时间序列内每一时刻已轧块数与预测剩余轧制块数之间的数据对应关系.这一过程中y轴的数据意义，即设备健康评价尺度发生了变化，对于单工况Copula模型无碍，但若要联合多个Copula模型进行动态预测，需要保留VHI作为中间参数，用于不同工况间的等效换算，以及设备真实寿命极限的评估.

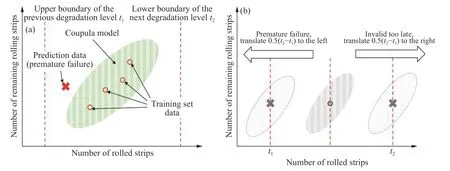
图8 提高模型适应性的平移处理.（a）过早失效时Copula模型无法预测；（b）Copula模型平移Fig.8 Translation processing to improve model adaptability: (a) Copula model is unpredictable at premature failure; (b) translation of copula model

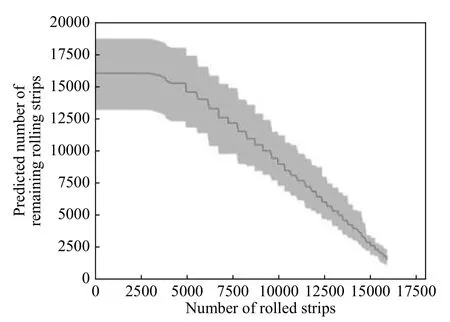
图9 单工况VHI预测结果Fig.9 Single-condition VHI prediction result

基于以上考虑，希望将各工况单独的预测结果统一还原为VHI尺度，以便各工况预测结果的相互融合，同时避免一次人为干预.图9中的横纵坐标分别为每一个预测点的已轧制块数与剩余轧制块数，理论上二者之和为一定值，由此可以给出VHI转化公式如下：其中x为预测点已轧制带钢块数，y为预测点剩余带钢轧制块数，∆y0m为第m个训练集数据的VHI分布范围，公式等号左边为预测点转换求得的VHI数值.

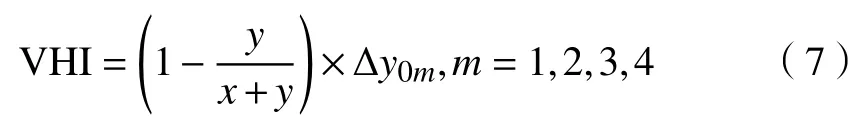
将各工况Copula模型的预测结果代入式（7）中，得到单工况预测结果的VHI尺度描述如图10所示，其中阴影部分代表VHI预测值的最大最小值范围，阴影中间的实线为预测点对应的预测值，可见描述尺度的变化并未对预测结果的趋势造成任何改变.

图10 经过VHI变尺度处理的单工况预测结果Fig.10 Single-condition VHI prediction result after scale conversion

4.2 复杂工况预测结果融合

解决各工况预测结果的评价尺度问题后，即可按照测试数据集的轧制计划融合各工况的单独预测结果.考虑轧件在轧制周期不同阶段对支持辊健康程度的影响差异，利用各预测点邻域范围内的VHI数据计算支持辊短期健康退化率描绘其衰减路径，具体流程如下：

第一步：将各工况模型预测结果全部转换为VHI尺度，并按照先前聚类结果划分测试数据集内各个样本的工况，完成准备工作；

第二步：按轧制计划序列进行预测结果融合，选择测试集数据点对应工况对应位置邻域内的数据按一次拟合方式计算短期健康退化率，求得该点退化率后描绘单位步长（单块带钢）的融合退化曲线；其中融合预测结果的起点由测试集轧制计划第一块带钢的设定参数计算VHI值得来，当预测数据点处于轧制单元头尾位置时邻域范围不变；

第三步：往复进行第二步工作，完成测试集全长的退化曲线，由于测试集数据点在轧制周期内位置不同，相同工况各点的健康状态退化率也会存在差异；

第四步：待融合预测曲线描绘一定长度后，其预测结果趋于稳定准确，分析预测性能衰减曲线，可以为生产计划排布、检修时机安排等提供参考.

4.3 现场生产数据验证

将数据集数据按照交叉验证方法轮流作测试集，按照上述过程融合得到复杂工况预测结果共5组，如图11所示.最终结果与构建的VHI曲线形貌相似，当预测VHI到达0.7时，对应的轧制块数范围在13233～15253块之间，可见轧制计划的不同对支持辊的寿命衰减影响明显，每块带钢由于所属工况及在生产计划中位置不同，对支持辊健康状态的消耗是不同的.测试集所使用的数据来自现场生产实况，最后一块带钢下线时支持辊的VHI并未达到理论极限值，这是由于现行维护策略综合考虑现场检修时机和后续轧制计划安排的情况下支持辊未充分使用，导致VHI在实际应用中不能达到理论极限.

对预测模型的计算结果进行评价，考虑到实际VHI数值的带状特性，取最后一个工作辊换辊周期，根据弯窜辊数据计算每块带钢轧制后支持辊的实际VHI，并求平均值作为实际下机VHI.模型预测VHI取轧制计划最后一块带钢下机时的模型融合预测结果.对比5组融合预测结果的对比情况如表2所示，可见预测误差均在10%以内，效果理想.

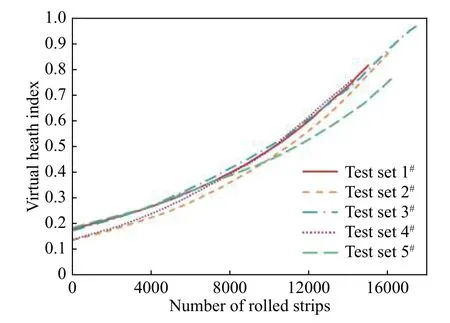
图11 融合预测结果示意图Fig.11 Fusion prediction result diagram

表2 复杂工况下Copula模型融合预测结果Table 2 Copula model fusion prediction results under complex conditions

融合结果误差的产生原因除模型预测误差外，还与VHI数据的带状分布特征有关.若将该模型应用至现场生产，可以在支持辊使用末期预测多种轧制计划下的剩余VHI，考虑轧辊磨损对弯窜辊设定值的影响，选择合适的排布方案将支持辊使用至预测VHI接近0.9时再安排换辊，最大化利用其健康寿命，以此有效提升支持辊健康状态下的轧制块数，节省停机时间，说明支持辊Copula模型对支持辊换辊时机的安排具有积极意义.

5 结论

（1）考虑支持辊濒临失效时板形调控手段到达极限的特点，使用某钢厂F7机架弯窜辊数据构建虚拟健康指标表征支持辊的健康状态，并将带钢的宽厚比和变形抗力两维数据带入K-means聚类算法，完成了轧制工况的划分，经过工况划分的训练集数据带状分布特征明显减小；

（2）由于支持辊的换辊周期较长，训练集能够使用的数据条目较少，传统的数据预测方法如神经网络等并不适用于这类情况.利用Copula函数的特性将其应用于数据预测中，利用少量数据集找到其符合的分布形式，使得数据量得以扩充，能够顺利完成单工况下支持辊剩余健康状态的预测，证明基于Copula函数的预测方法在训练数据集稀少的情况下具有优势；

（3）结合各单独工况下支持辊剩余健康状态的预测结果及现场生产轧制计划，将复杂工况混合轧制情况下支持辊剩余健康状态的预测结果融合，并在最后利用预测结果提出了最大化利用支持辊健康寿命的换辊策略，证明了预测模型的适用性和准确性，该流程同样适用于钢铁生产领域中其他关键设备的寿命预测问题.