铝合金管材6061自由弯曲成形工艺仿真及优化

2020-07-06李玉森岳振明妥之彧闵鑫瑞

工程科学学报 2020年6期

李玉森，岳振明，妥之彧，闵鑫瑞，高军

山东大学（威海）机电与信息工程学院，威海 264209

金属管材在众多工业领域中发挥着重要作用，比如：航空航天、高铁、船舶、汽车、桥梁结构和建筑等领域[1−2].特别强调的是弯管构件可以在航空器系统中承担输送液态或气态介质的重要角色[3−4].然而，对于轴线空间复杂，曲率不断变化的弯曲构件，传统弯管工艺实现较为困难.近年来，管材自由弯曲成形技术逐渐成为塑性成形领域的热点，该技术可以实现精确无模弯管，有效地节省模具设计生产环节，降低生产成本，实现节能和设备的轻量化[4].同时，自由弯曲成形动作连续，能有效地避免应力应变的过度集中，因而弯曲获得的试件质量优异，具有较长的使用寿命.

管材自由弯曲成形技术带来优势的同时，也对其工艺提出了更高的要求，比如：固定模与移动模间的距离，移动模截面形状、偏移量，移动模与管材外表面间隙大小、摩擦系数，管材进给速度.不合理的弯曲工艺容易造成管材成形件的起皱、破裂以及回弹过大等问题[5−6].Gantner等[7−8]对管材自由弯曲成形过程进行了有限元模拟，并将模拟结果与实验结果进行对比，优化了自由弯曲成形工艺.该工艺几乎可以弯曲成形任意轴线形状的复杂弯管，但最大缺陷就是管材的弯曲成形半径至少要是管材半径的2.5倍.Plettke等[9]对该工艺的技术原理进行了系统的介绍.Goto等[10]通过实验研究了移动模偏移量u与弯曲半径的倒数1/R的线性关系，确定了移动模与管材外表面间隙大小以及移动模的偏转角度对空间自由弯管的成形半径的重要作用.Kawasumi等[11]则研究了模具间隙及回弹对成形的影响.Li等[12−13]应用有限元方法对不同截面的高强钢自由弯曲成形过程进行了仿真模拟分析，发现在固定模与移动模距离相同的情况下，管材弯曲成形半径随移动模偏移量的增加而减小；当移动模偏移量相同时，固定模与移动模距离越小，管材成形半径越小.Yang等[14]通过对弯曲特性及缺陷的分析，研究了管材自由弯曲成形中内弧面起皱，外弧面变薄、开裂，弯曲回弹，截面变形等的常见问题.Wu等[15]对自由弯曲成形的管材回弹现象进行了研究，提出将空间变曲率弯管离散成许多小的平面圆弧段，为空间变曲率弯管的回弹预测及补偿打开了新思路.Guo等[16]研究了自由弯曲成形工艺的解析方法，并对影响管材的自由弯曲成形的工艺参数(移动模间隙、固定模圆角等)进行了有限元仿真模拟及实验研究，确定了部分工艺参数特别是固定模与移动模间的距离对最终成形管件的影响规律.

本文针对管径30.0 mm，壁厚2.0 mm的铝合金管材6061，首先通过基础拉伸实验及压弯实验，确定并验证铝合金管材的有限元仿真模型（FEM）的有效性.而后，结合FEM研究自由弯曲过程中的移动模与管材间隙大小、摩擦系数和管材进给速度等工艺因素对管材最终成形效果的影响规律，确定出该工况下工艺参数的最优值，为铝合金管材6061的自由弯曲成形工艺提供理论指导.

1 管材自由弯曲成形工艺解析

传统的管材弯曲成形过程如图1（a）所示，成形过程中主要依靠弯曲模，且需要根据不同的管材半径和弯曲半径更换弯曲模.管材的自由弯曲成形相对传统弯管过程要更为复杂，其原理如图1（b）所示.该工艺主要有三个构件：推进机构、固定模以及移动模.推进机构主要实现管材的送管过程，通过调节移动模和固定模的相对位置实现不同曲率弯管的成形.推进机构推力和移动模横向移动产生扭矩使管材发生自由弯曲成形.其中，移动模与固定模的距离L和移动模的横向偏移量u共同决定了管材的弯曲半径.距离L越小，偏移量u越大，获得管材的弯曲半径就越小.管材获得弯曲半径R和弯曲力矩M的计算方法如公式（1）所示：

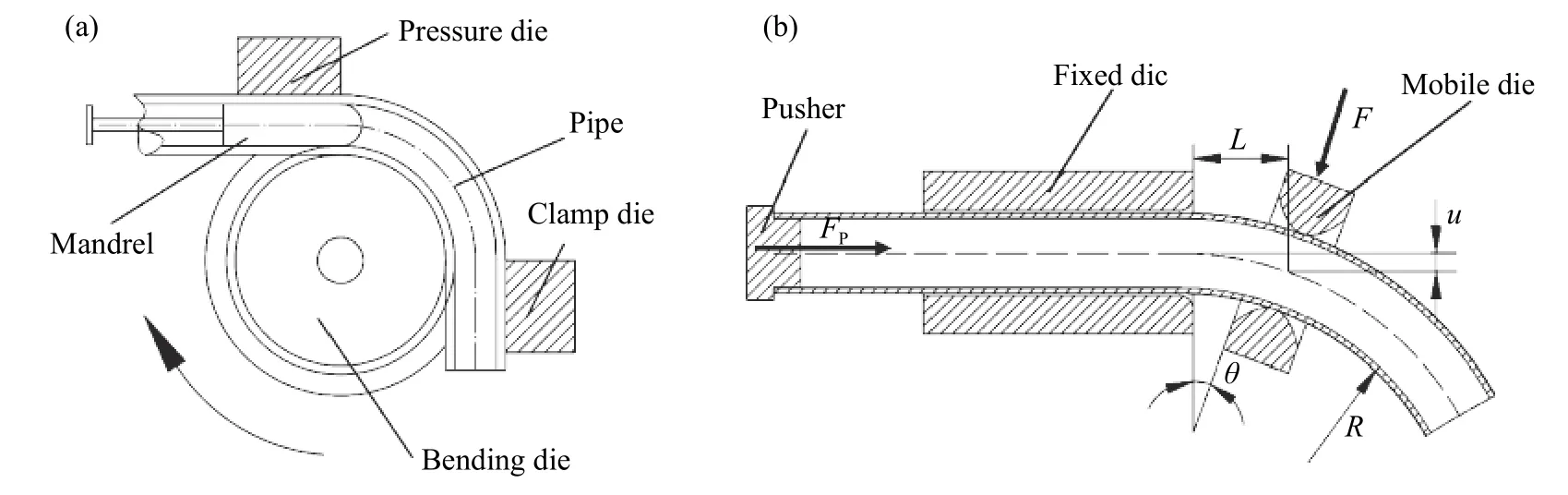
图1 弯管工艺外对比.（a）传统弯管；（b）自由弯管Fig.1 Comparison of tube bending processes: (a) traditional technique; (b) free bending

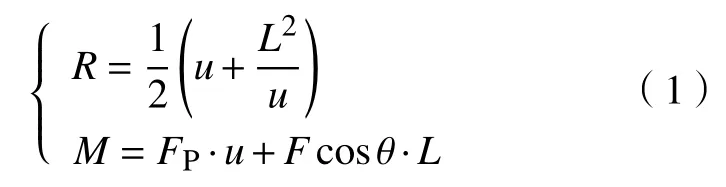
式中，FP为推进机构的推力，F为移动模的弯曲力，θ为移动模的偏转角度.

2 实验材料性能提取与仿真模型的建立

本文选用直径为30.0 mm，壁厚为2.0 mm的铝合金管材6061.为获得该管材的基本力学特征用于后续的自由弯曲仿真模拟，分别沿管材轴向和环向方向制备拉伸试样，在万能试验机上开展拉伸实验，拉伸速度2.0 mm·min−1，如图2所示.获得材料的弹塑性力学数据用于仿真本构模型的参数表征.同时，结合管材的压弯实验验证模型参数的有效性.

通过仿真结果与实验结果对比发现，在不考虑材料各向异性的情况下，轴向和环向的拉伸仿真结果与实验结果能较好的吻合.需要强调的是由于环向拉伸的应变不易测量，因此对比了力和位移曲线.同样，压弯过程通过对比力和位移曲线，验证了该模型在预测管材弯曲成形过程的有效性.因此在后续的自由弯曲过程中将采用表1中的模型参数开展仿真模拟和工艺参数优化.

3 仿真结果分析及工艺参数优化

3.1 典型自由弯曲成形仿真分析

图2 铝合金管材6061拉伸实验及压弯实验.（a）轴向拉伸；（b）环向拉伸；（c）压弯Fig.2 Tensile test and press bending test of aluminum alloy 6061 pipe: (a) axial tensile test; (b) circumferential tensile test; (c) press bending test

表1 铝合金管材6061模型参数Table 1 Model parameters of aluminum alloy 6061 pipe

图3 实验与仿真结果对比.（a）轴向拉伸；（b）环向拉伸；（c）压弯Fig.3 Comparison between the simulation and experimental results: (a) axial tensile test; (b) circumferential tensile test; (c) press bending test

图4 自由弯曲成形有限元仿真几何模型Fig.4 Finite element geometrical mode of free bending forming

自由弯曲成形的有限元几何模型如图4，该模型包含：推进机构、固定模、移动模和管材四部分.推进机构、固定模和移动模可定义为刚体，管材采用可变形体壳单元，网格类型选择S4R，最小单元尺寸1 mm，外载荷边界条件设置如下：固定模和移动模的距离为90 mm，移动模向上偏移50 mm的同时偏转58◦，推进机构以20 mm·s−1的速度匀速送料，各部件之间摩擦系数定义为0.1.自由弯曲成形后的应力、应变及壁厚云图如图5所示.管材弯曲外侧、内侧及中性层处沿管材进给长度的应力应变及壁厚变化如图6.

通过观察管材自由弯曲成形后的应变应力云图可以发现：管材在移动模的作用下从直线型逐渐被弯曲成曲线型，管材应力分布均匀，无应力集中.外弧侧受拉变形产生较大的拉应力，而内弧侧因为自身材料的堆积产生较大的压应力；由于管材内外弧侧均受到较大应力，故都发生较大的应变如图6.同时，管材外弧侧受拉应力，壁厚减薄；内弧侧因材料堆积，管材壁厚增大，中性层附近壁厚近乎不变，如图5所示.管材外侧壁厚减薄将影响管材的使用寿命，甚至直接导致管材外壁破裂.因此，管材壁厚减薄率将作为下文对管材参数优化的一项重要指标，目前在常用领域内认为铝合金管材壁厚减薄率不超过6%为正常现象.外弧侧壁厚虽然整体趋势为减薄，通过观察发现弯曲初期也会发生壁厚增加现象，这是由于变形初期，管材外弧侧与移动模接触，移动模阻碍了管材外侧的材料流动，同时移动模的偏移量较小，对管材施加的弯矩也较小，因此该阶段管材外弧侧壁厚有增大的趋势.

图5 自由弯曲成形后的应力、应变及壁厚云图Fig.5 Stress, strain, and thickness nephogram of free bending forming

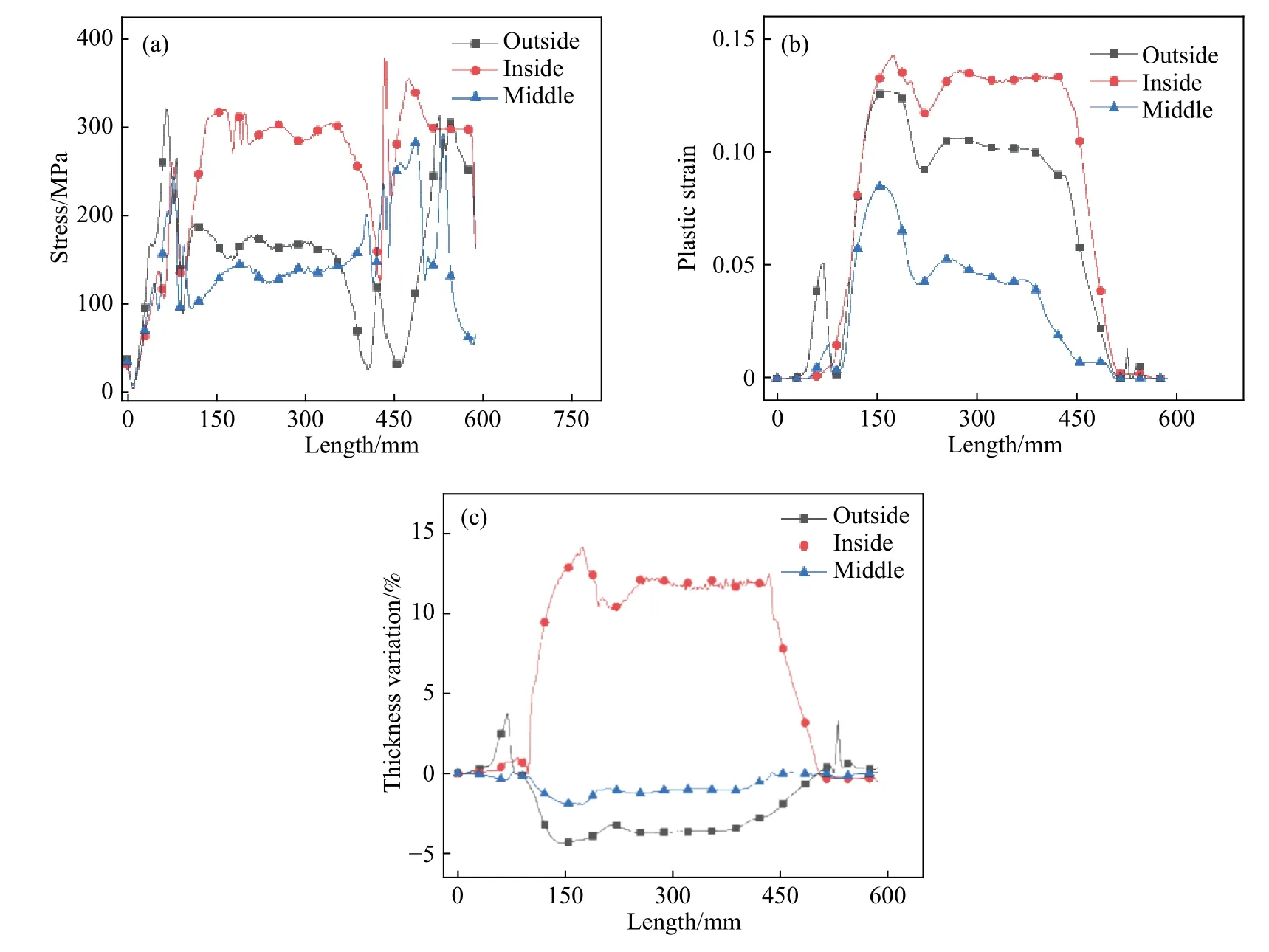
图6 沿管材进给长度的应力应变及壁厚变化曲线.（a）应力；（b）应变；（c）壁厚Fig.6 Stress, strain and thickness curve of bending along the feed length of pipe: (a) stress; (b) strain; (c) thickness

管材截面的椭圆度Θ是衡量管材弯曲成形后质量的重要指标，在行业领域内，截面椭圆度不超过8% 即可被接受.因此，在本研究中将选择椭圆度作为重要的优化指标，椭圆度Θ计算方式如公式（9）和图7所示.

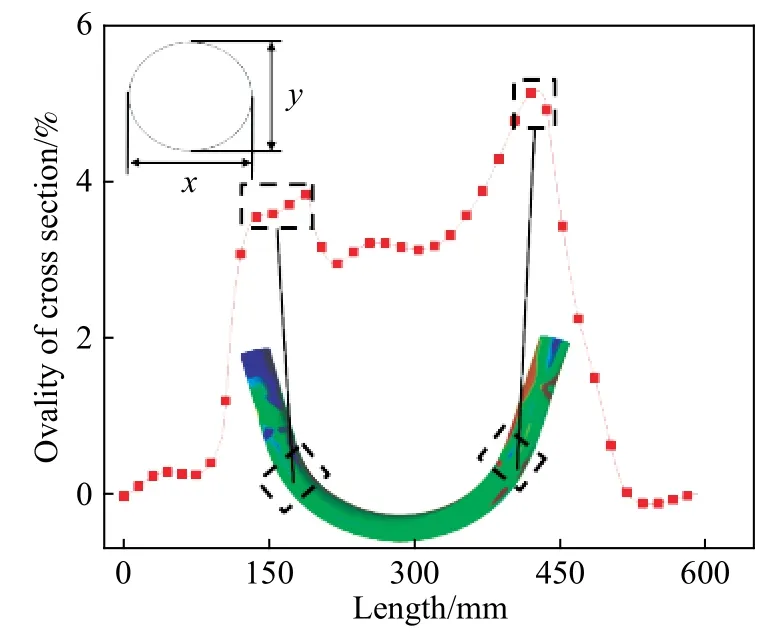
图7 管材截面椭圆度Fig.7 Ovality of pipe section

式中，x为椭圆长轴长度，y为椭圆短轴长度.图7所示为管材沿进给方向的截面椭圆度变化曲线，由图可知管材在由直线段进入圆弧段或圆弧段进入直线段时截面变形较大.

本文经过研究分析最终确定固定模与移动模的距离为90 mm.在固定模与移动模距离恒定情况下，移动模偏移量u将对管的成形半径R产生重要影响.本文选取u为10，20，30，40，50，和 55 mm 6组参数进行仿真和对比分析，结果如图8所示.随着偏移量u的逐渐增大，管材的弯曲半径逐渐减小.通过对不同偏移量成形半径的分析，可以得出自由弯曲成形的曲率1/R同偏移量u呈线性关系.本文的目标弯曲半径为管材直径的3.5倍（105 mm），依据拟合得出的曲率与偏移量的线性关系，移动模的偏移量u为58 mm.下文也将以此偏移量对工艺参数进行优化分析.

3.2 管材与移动模间隙的参数优化

图8 不同移动模偏移量下的成形结果Fig.8 Forming results with different offsets of mobile die

管材与移动模的间隙对管材成形质量有较大影响，间隙较小时移动模对管材材料流动的阻碍较大，间隙较大时移动模对管材的约束作用又将减小.因此，确定管材与移动模的间隙大小对提高自由弯曲成形件的质量十分重要.图9展示了间隙c分别为 0, 0.1, 0.2, 0.3和0.4 mm下管材成形结果.从图9（a）中可以发现，随着间隙的增大，管材的成形半径逐渐增大.由图9可知，在间隙为0即管材和移动模无间隙时，移动模严重阻碍管的材料流动，因此壁厚减薄率最大且明显的波动，而截面椭圆度却变化最小.同时，随着间隙的减小，移动模对管材的阻碍作用将随之增大，因此需要更大的推进力，如图9（d）所示.间隙越小推进力越大，在间隙为0时的推进力远大于其他间隙下的推进力，且波动很大.另一方面，移动模与管材的间隙越大，移动模对管材轴向材料流动阻碍作用就越小，因此管材的平均应变、壁厚减薄率都随间隙的增大而减小；与此相反的，间隙越大时移动模对管材的约束作用减弱，对沿管材圆周方向的材料流动阻碍减小，管材沿截面椭圆长轴方向变形趋势增大，因此管材的截面椭圆度随间隙的增大而增大，如图10（a）所示.由图10（b）可知，当间隙c= 0.2 mm时，残余应力最小，当间隙c＞ 0.2 mm后，管材成形后的平均应变将趋于不变.且当间隙c= 0.2 mm时，管材最大截面椭圆度不足5%，在可接受范围内.因此综合考虑来看，推荐选择管材与移动模的间隙为c=0.2 mm.

3.3 管材与移动模摩擦力的参数优化

管材与移动模间的摩擦力是影响自由弯曲成形的另一工艺参数.为了研究摩擦力对管材成形质量的影响，本文对管材与移动模间的从无摩擦到摩擦系数为0.5进行了有限元仿真分析.图11（a）为不同摩擦力下管材自由弯曲成形结果图，由图可知，摩擦力对管材自由弯曲成形半径影响不明显.图11（b）和（c）展示了不同摩擦系数下，管材成形后残余应力、推进力、壁厚减薄率以及截面椭圆度的变化.由图11（b）可知，摩擦力对管材成形的壁厚变化影响很小，壁厚变化的平均差值仅为0.03%，可忽略不计.根据最小阻力定律，变形体内的质点将沿阻力最小的方向移动.由于移动模和管材之间存在间隙，管材内部材料流动的方向如图12所示，造成管材截面形状椭圆化.横截面内管材受到移动模的摩擦力方向与材料流动方向相反.即移动模与管材间的摩擦力阻碍材料沿移动模内壁方向流动，抑制管材截面椭圆化的发展，且摩擦力越大抑制作用越明显.因此，随摩擦力的增大，管材截面畸变程度越低，如图11（b）.

图9 不同间隙的成形结果.（a）应变云图；（b）壁厚变化曲线；（c）截面椭圆度变化曲线；（d）推进力变化曲线Fig.9 Results of bending with different clearance: (a) strain contour; (b) thickness curve along the feed length of pipe; (c) ovality curve along the feed length of pipe; (d) pushing force curve

图10 壁厚、椭圆度、残余应力和应变变化曲线.（a）平均壁厚减薄率和截面椭圆度；（b）残余应力和应变Fig.10 Thickness reduction, ovality, residual stress and strain curve of bending: (a) thickness reduction and ovality; (b) residual stress and strain

图11 不同摩擦力下成形结果.（a）成形云图；（b）平均壁厚减薄率和截面椭圆度变化；（c）残余应力和推进力变化Fig.11 Results of bending with different frictional coefficients: (a) forming nephogram; (b) average thickness reduction and ovality; (c) residual stress and pushing force

图12 管材材料流动方向及摩擦力方向示意图Fig.12 Direction of material flow and frictional force

另一方面，摩擦系数越大即移动模和管材间的摩擦力越大，移动模对管沿轴向的阻碍作用就越大.因此，管材进给所需的推进力也随摩擦系数的增大迅速增大，这就对成形设备提出了更高的要求.同时，由于移动模对管材轴向方向材料流动性的阻碍，使得管材内部变形不均匀性升高.因此，随摩擦系数的增大，管材成形后的残余应力也迅速增加，如图11（c）.尽管摩擦力越大，管材截面椭圆度越小，但远不如摩擦力对残余应力和推进力的影响明显.综合考虑来看，本文推荐选择管材与移动模间的摩擦系数为f=0.1.此时，成形后的管材平均截面椭圆度为3.7%，处于截面变形较低程度.同时，管材进给所需推进力和变形后的残余应力也均较低.

3.4 管材进给速度的参数优化

管材的进给速度和管材的成形效率密切相关，较大的进给速度意味着较高的成形效率.因此，找到一个最佳的进给速度显得十分重要.本节将主要对5～800 mm·s−1的不同进给速度进行仿真分析来研究进给速度对自由弯曲成形工艺的影响.图13展示了当固定模与移动模的距离L为90 mm，移动模的偏移量u为40 mm 时，管材不同进给速度成形后的残余应力、推进力、壁厚减薄及截面椭圆度变化.由图13可知，在一般成形时管材进给速度对成形结果影响不大.图14所示为固定模与移动模的距离L为90 mm，移动模的偏移量u为60 mm时，管材进给速度分别为5和50 mm·s−1时的成形结果.显而易见的，当进给速度为50 mm·s−1时，管材发生了压瘪现象.考虑到是由于较大的进给速度让管材产生较大的应变速率，而较大的应变速率致使管材塑性能力降低，造成上述现象.

图13 不同速度下应力、推进力、壁厚和椭圆度变化曲线Fig.13 Stress, pushing force, thickness, and ovality curve with different velocities

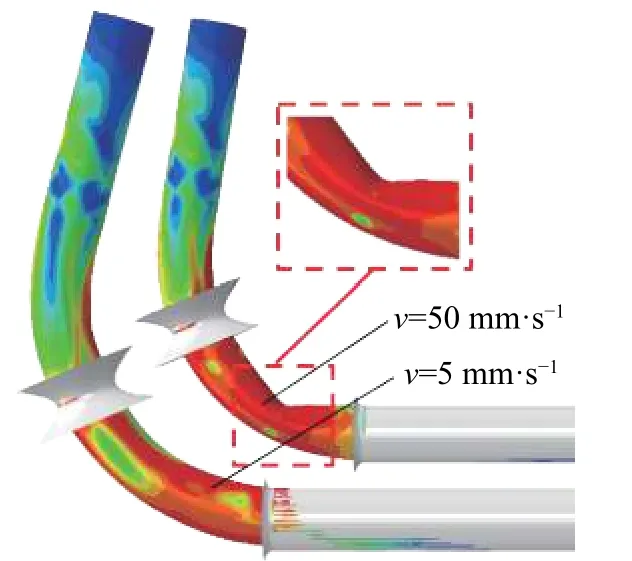
图14 5和50 mm·s−1进给速度的成形结果Fig.14 Forming result of bending with different velocities

为进一步研究进给速度对管材成形质量的影响，对不同速度下能够加工满足要求（壁厚减薄率不超过6%，截面椭圆度不超过8%）移动模的最大偏移量，即管材的成形极限进行了分析，结果如图15所示.考虑到弯曲半径与管材直径比3.5的成形目标以及较大加工效率，选择速度v= 20 mm·s−1作为自由弯曲成形管材进给速度.