鳍条倾角对仿生鳍推进力大小的影响
2016-12-23章永华
章永华
(台州职业技术学院 机电工程学院, 浙江 台州 318000)
鳍条倾角对仿生鳍推进力大小的影响
章永华
(台州职业技术学院 机电工程学院, 浙江 台州 318000)
为研究仿生鳍条倾斜角度对波动鳍推进力产生的影响, 建立了鱼鳍运动学和动力学方程. 通过实验测量技术, 比较分析了仿生鳍在等鳍条长度和等鳍面面积两种情况下, 鳍条倾角分别为30°, 40°, 45°, 50°, 60°, 70°, 80°和90°时推进力的变化规律, 同时测量了鳍条倾角为45°时不同运动学参数下两种模式的推进力. 并从流体动力学角度, 初步解释了两种情况下仿生鳍推进力存在差异的原因. 结果表明: 在等鳍条长度条件下, 平均推进力随着鳍条倾角的增大而增加; 在等鳍面面积条件下, 平均推进力随着鳍条倾角增大而减小. 在相同条件下, 等鳍面面积仿生鳍产生的平均推进力始终大于等鳍条长度情况. 该结果为仿生波动鳍推进器结构优化提供参考.
波动鳍; 鳍条倾角; 推进力; 计算流体动力学
水下生物大都依赖于身体的某些部位运动, 在尾迹区域产生反卡门涡街或形成射流实现诸如前行、 转弯、 快速启停等巡游和机动性游动. 如金枪鱼的鱼体和月牙形尾鳍波(摆)动, 鳐鱼的一对硕大外延胸鳍波动, 章鱼则靠挤压体内流体形成射流推进. 中间鳍/对鳍(Medial and Paired Fin, MPF)推进模式具有极高的游动稳定性和机动性, 由于其本体姿态在游动过程中基本保持不变, 因此, 仿MPF推进模式的水下推进器更容易装载测量仪器进行科学探测和有关的应用研究, 或更能实现未来的水下载人[1]. MPF模式游动的生物因其独特的优势而越来越受到仿生工程领域研究人员的关注.
迄今, 国内外针对MPF模式的仿生水下推进器的研制已有十多年, 产生了一批具有良好性能和实用价值的研究成果. 2001年, 英国Heriot- Watt大学的Sfakiotakis等人利用并联的膜盒致动器(Parallel Bellows Actuator, PBA)作为鳍条研制了仿生长期波动推进装置[2], 掀起了MPF模式推进器研制的热潮. 之后, 研究人员或是利用传统的电机作为驱动源[3-10], 或是利用智能材料(Smart Material), 如人造肌肉[11]、 形状记忆合金(SMA)[12-14]、 高分子离子聚合物(IPMC)[15-16]等开发了模仿各种类型MPF模式鱼类的水下推进装置, 并针对这些MPF模式开展了各类理论[17-21]、 数值分析[4, 22-24]和实验研究[1, 25-27]工作.
仿生对象的解剖学研究发现: 几乎所有依赖鳍波动推进的鱼类(如: 鳐鱼), 其鳍条与根部连接软骨夹角一般都没有严格垂直. 本文针对仿生波动鳍推进器, 利用实验测试技术, 对等鳍条长度和等鳍面面积两种条件下, 仿生鳍产生的推进力随不同鳍条倾角的变化情况进行深入的研究. 并从流体动力学角度, 初步解释两种情况下仿生鳍推进力存在差异的原因. 为仿生波动鳍选择合适的鳍条倾角最大程度地提高推进力和效率提供参考.
1 建 模
1.1 运动学建模
本文在鳍条长度不变和鳍面面积不变两种情况下, 分析鳍条倾角变化对波动鳍推进力大小的影响, 如图 1 所示, 此处将鳍条倾角定义为仿生鳍鳍条与根部固定座间夹角. 值得注意的是: 在鳍条长度不变条件下, 鳍面面积随鳍条倾角的增大而减小; 在鳍面面积不变条件下, 鳍条的长度将发生改变, 且长度随着鳍条倾斜角度增大而增大. 由于鳍面面积未变, 故波动鳍迎水面面积以及和流体接触面面积均不随鳍条的倾角而改变.
鳍条倾角的变化将导致仿生鱼鳍的鳍面波动方程的改变, 如图 2 所示, 在笛卡尔直角坐标系oxyz下, 以仿生鳍根部基线作为x轴. 为简化模型, 假设鱼鳍初始时刻位于oxz平面内. 第n根鳍条在倾角θ时根部坐标为(x0,z0), 端部坐标为(x,z), 其摆动方程表达式为
式中:A为与z坐标和倾角θ有关的摆幅;φ为初始相位.
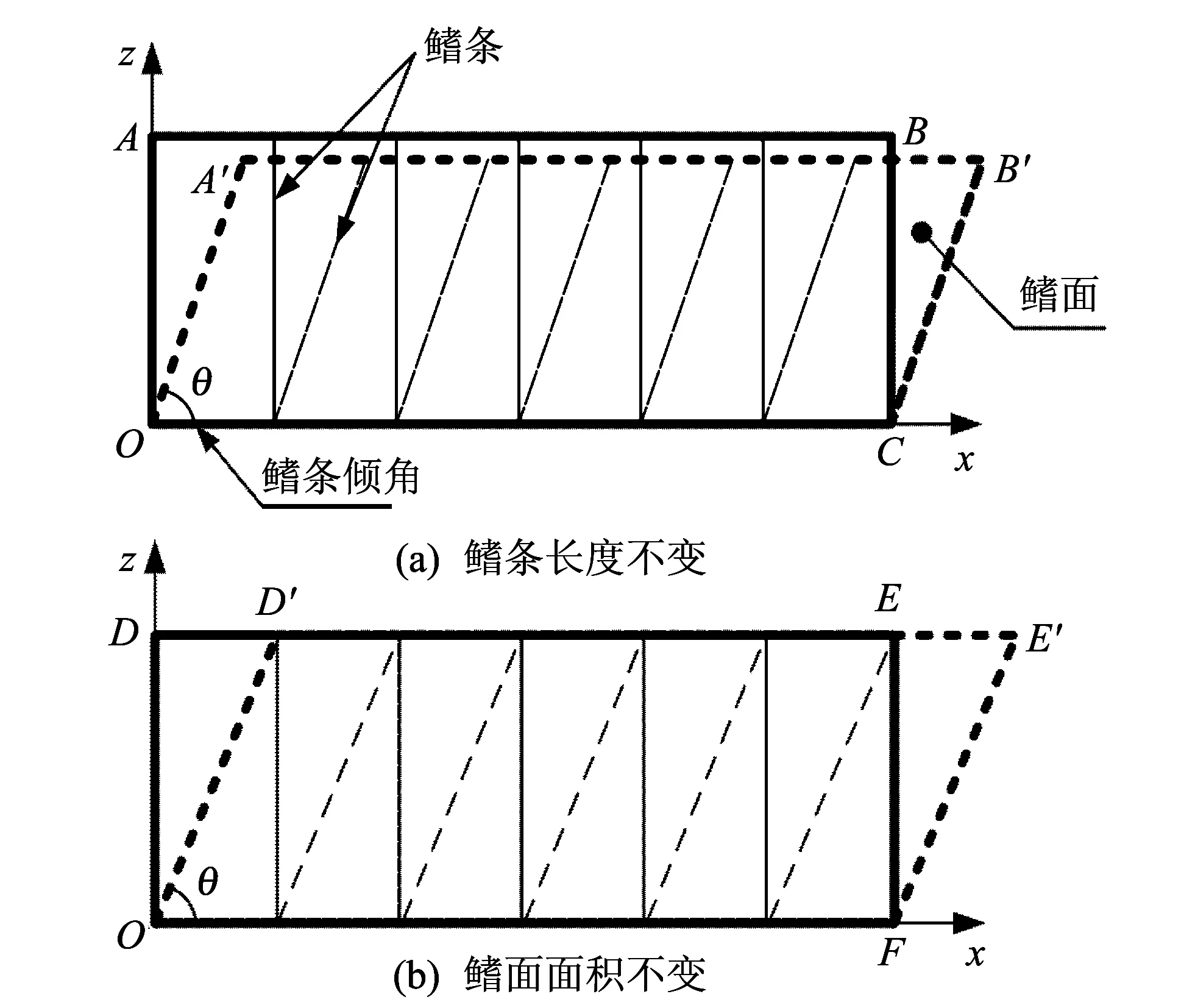
图 1 鳍条倾角改变下的两种情况Fig.1 Two cases with change of fin ray angle

图 2 运动学建模Fig.2 Kinematic modeling
由于θ=π/2时鳍条的运动学方程为
式中:λ为波长;T为周期;k为斜率;x′和z′表示θ=π/2时鳍条端部坐标参数.
根据图中几何关系有
θ.
由于z0=0, 则
此外
将式(3),式(4)代入式(2), 得到
式(5)即为鳍条倾角θ时的摆动方程.
1.2 动力学建模
为了建立仿生鳍动力学方程, 对其进行如下4点简化: ① 忽略鳍条和蒙皮的质量; ② 忽略鳍条和蒙皮的厚度; ③ 忽略鳍条的柔性变形; ④ 鳍面长度保持不变. 在此基础上, 得到推进力的计算式为
‖
式中:F(t)作用于鱼鳍表面的推进力;ρ流体密度;Cd阻力系数;S仿生鳍迎水面面积;υ为相对于流体的运动速度;uv运动方向单位矢量.
F(t)可进一步分解为作用于鱼鳍表面的切应力和正应力. 由于鱼鳍运动在高雷诺数范围, 水的流体粘性影响很小, 因此, 由流体粘性导致的切应力相对正应力而言可以忽略不计, 分析流体作用时只考虑其中正应力作用的影响. 式(6)作如下近似处理
式中:F⊥由正应力产生的惯性力;u⊥垂直于鳍面单位速度矢量.
针对波动鳍的运动特点, 考虑第i-1根鳍条和第i根鳍条间鳍面微元ds受力情况, 在图 3 所示坐标系下有
其中,
υ(xr,Ls,t)=ωf(xr,t)Ls,
ωf(xr,t)=

f(xr)=f(x)|x=xr,
式中:ωf为xr位置处鳍条摆动角速度;f(x)为鳍面波幅分布函数;T为运动周期;λ为波长;Ls为鳍面微元离根部距离;Lrq为xq处鳍面宽度. 代入式(8), 并对鳍面oi-1AiAi-1积分, 则整个鳍面承受正应力为


图 3 动力学建模Fig.3 Hydrodynamic modeling
arcsin(f(xr)/Lrq)对于确定的波幅分布函数而言为常数, 因此, 式(9)可以进一步简化为
式中:ξ为鳍条间距;xi为第i根鳍条在鳍面坐标系oqxqyqzq的坐标值;xi-1为第i-1根鳍条在鳍面坐标系oqxqyqzq的坐标值. 则一个周期内该鳍面产生的平均推进力为
式中:Ftotal一个周期内平均推进力;T为周期.
2 实验测量装置及原理
仿生鳍推进力测量的实验装置如图 4 所示. 该装置主要包括长×宽×高为4.5 m×2 m×1.8 m 的水槽、 六分量测力传感器、 固定架、 数据采集器(型号: M8128)和用户软件. 仿生鳍通过连杆与测力传感器固连, 传感器输出信号由19针LEMO接口进入数据采集器, 该数据采集器采样频率2 kHz, AD转换精度为24位, 供电电压12~36 V. 随后数据通过RS232接口传输至电脑, 由用户软件记录并显示.

图 4 实验测试装置Fig.4 Experimental testing system
根据采样获取的数据计算平均值推进力
实验首先测量了运动学参数固定为波长0.75, 频率4 Hz, 幅度0.1时, 鳍条倾角分别为30°, 40°, 45°, 50°, 60°, 70°, 80°, 90°两种情况下推进力的大小. 最后对比研究了鳍条倾角为45°时, 两种情况下不同运动学参数的影响. 各参数取值如表 1~表 3 所示.

表 1 鳍条倾角参数取值

表 2 仿生鳍几何参数

表 3 运动学参数取值
3 实验结果
3.1 平均推进力随鳍条倾角的变化情况
等鳍条长度和等鳍面面积下平均推进力随鳍条倾角的变化情况分别如图 5 和图 6 所示. 从实验测试结果看: 在等鳍条长度条件下, 平均推进力随着鳍条倾角的增大而增大, 在倾角为30°时, 平均推进力约为1.65 N, 倾角为90°时平均推进力达到2.54 N; 而等鳍面面积下的平均推进力随鳍条倾角增大反而减小, 在实验测量范围内, 倾角为30°时, 平均推进力约为2.88 N, 倾角为90°时平均推进力降低至2.54 N. 另外, 等鳍条长度条件下, 平均推进力始终随着倾角的变化近似线性增加; 但是, 等鳍面面积下平均推进力随鳍条倾角的变化则有些不同: 在45°~90°倾角范围内, 随着倾角的减小, 推进力近似线性增大, 在30°~45°倾角范围内, 平均推进力增加的幅度显著降低. 而且相同运动学参数下, 等鳍面面积仿生鳍产生的平均推进力始终大于等鳍条长度的推进力.
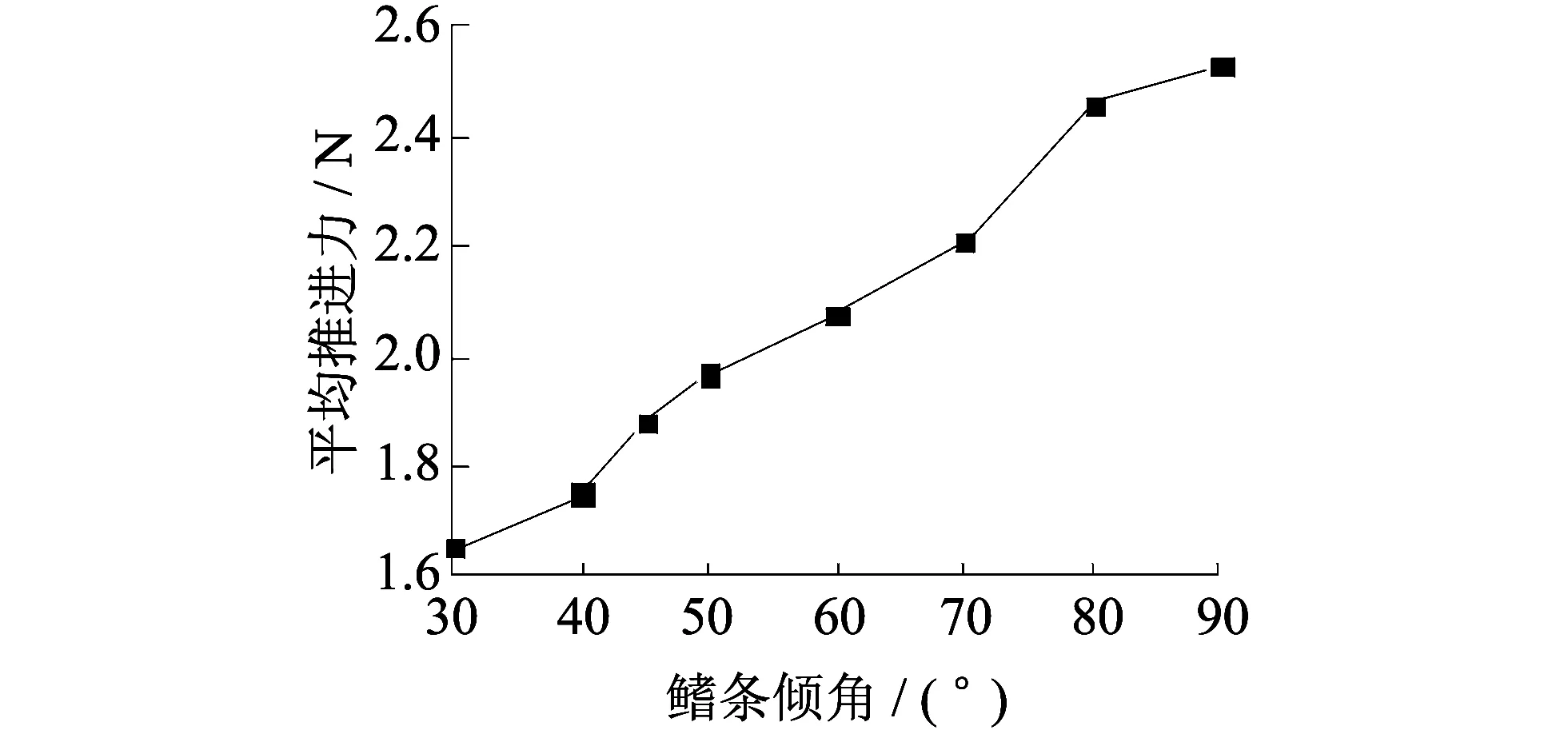
图 5 等鳍条长度下平均推进力随鳍条倾角的变化情况Fig.5 The change of averaged thrust with different fin ray angle in the case of constant fin ray length

图 6 等鳍面面积下平均推进力随鳍条倾角的变化情况Fig.6 The change of averaged thrust with fin ray angle in the case of constant fin surface area
3.2 平均推进力随运动学参数的变化情况
图 7~图 9 所示分别为鳍条倾角45°时平均推进力随频率、 摆幅和波长等运动学参数变化情况. 从结果看, 平均推进力随着频率、 摆幅和波长的增加而增大, 且这种变化趋势在这两种情况下总体一致. 同样, 无论哪种运动学参数, 等鳍面面积仿生鳍产生的平均推进力均大于等鳍条长度仿生鳍产生的推进力.

图 7 45°倾角下平均推进力随摆动频率的变化情况(幅度=0.2, 波长=1)Fig.7 The change of averaged thrust with frequency at 45° fin ray angle

图 8 45°倾角下平均推进力随摆动幅度的变化情况(频率=2 Hz, 波长=1)Fig.8 The change of averaged thrust with amplitude at 45° fin ray angle

图 9 45°倾角下平均推进力随摆动波长的变化情况(频率=2 Hz, 幅度=0.2)Fig.9 The change of averaged thrust with wavelength at 45° fin ray angle
4 讨 论
利用文献[28]数值计算方法和条件, 对两种情况下鱼鳍表面压力分布和切面涡量分布情况进行分析, 初步揭示两种情况下仿生鳍推进力存在差异的原因.
4.1 鳍面压力分布情况
图 10(a)所示为t=1T时刻(T为波动周期), 鳍条倾角分别为30°, 40°, 45°, 50°, 60°, 70°, 80°和90°时, 等鳍条长度鳍面压力分布情况. 其中运动学参数取值为频率2 Hz, 摆幅0.2, 波长1. 左侧为压力数值指示色条, 图上线条为压力等高线. 从鱼鳍表面压力分布图可以看出: 高压区和低压区在鳍面上下表面交替出现, 且高压区出现在鳍面上的凸面处, 低压区出现在鳍面的凹面处. 这种高低压区域的分布将在鳍面上形成压力差, 是推进力产生的重要来源之一. 上下表面压力差越大, 压力方向与仿生鳍推进方向夹角越小, 则推进力越大. 另外还发现, 压力数值由鳍面端部向鳍面根部逐渐减小. 该现象与仿生鳍中鳍条的运动方式有关, 仿生鳍的波状运动由具有一定相位差的相邻鳍条绕各自根部摆动形成, 鳍条端部位移和线速度最大, 流体的反作用力也就越大. 另外, 随着鳍条倾角的增大, 正负压力的数值亦随之增加, 导致推进力随之增大.
图 10(b) 所示为相同运动学参数下等鳍面面积时鳍面的压力分布情况. 与等鳍条长度计算结果类似, 鳍面上同样出现高低压力区域的交替, 端部的压力变化剧烈程度明显大于根部附近区域. 不同的是: 在该条件下, 随着鳍条倾角的增大, 正负压力的数值反而变小, 导致推进力亦随之减小.

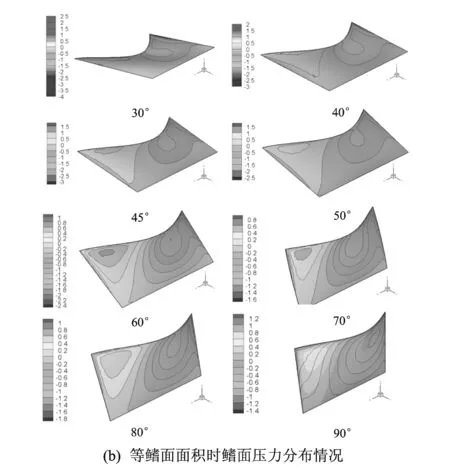
图 10 鱼鳍表面压力分布图(时间t=1 T, 频率=2 Hz, 幅度=0.2, 波长=1)Fig.10 Pressure contour of fin surface
4.2 平均无量纲阻力系数情况
无量纲阻力系数Cd综合体现了模型产生的推进力, 是压差阻力和摩擦阻力作用于鱼鳍表面的综合效果. 由式(6)知
则无量纲阻力系数的时间平均值为
m和j取值为0,1,2,3,…,t为时间.

从计算结果看: 随着鳍条倾角的增大, 等鳍条长度情况下, 仿生鳍无量纲阻力系数平均值从-0.06~-0.38变化, 显示推进力逐渐增大的趋势. 在等鳍面面积情况下, 鳍条倾角在30°时仿生鳍无量纲阻力系数平均值为-0.90, 倾角为90°时, 该值为-0.38, 表明推进力随倾角变大而减小. 上述结果与实验测试图 5 和图 6 结论相匹配. 另外, 在计算范围内, 等鳍面面积无量纲阻力系数平均值始终大于相同条件下等鳍条长度的值, 说明等鳍面面积仿生鳍产生的平均推进力始终大于等鳍条长度情况. 这一结论也与实验结果相符合.


图 11 无量纲阻力系数随鳍条倾角的变化情况Fig.11 The change of non-dimensional drag coefficient with fin ray angle
4.3 切面涡量分布情况
根据式(6)可知: 推进力的大小与仿生鳍迎水面面积成正比. 因此, 在等鳍条长度条件下, 由于参与运动产生推力的鳍面面积随鳍条倾角的增大而增加, 故推进力亦随之增加. 而等鳍面面积情况则有所不同, 在该情况下, 仿生鳍迎水面面积并不随着鳍条倾角的变化而改变. 图 12 给出鳍条倾角40°, 50°, 80°和90°时等鳍面面积条件下Z=0.03 m切面上的涡量分布.
结合不同倾角下鱼鳍运动形成涡量的分布情况(图12), 发现相同计算条件下, 随着倾角的增大, 仿生鳍尾迹区域形成的反卡门涡街逐渐变得不明显, 而该种形式的漩涡存在, 被认为是提高波动推进力和游动效率的重要原因之一; 另一方面, 倾角增大后, 计算区域内流场的涡街强度减弱, 故鱼鳍运动产生的射流强度减弱, 作用于鱼鳍表面用于形成推力的流体作用力值亦随之变小.

图 12 涡量分布图Fig.12 Vortex distribution
5 结 论
本文分析了鳍条倾角分别为30°, 40°, 45°, 50°, 60°, 70°, 80°和90°时, 等鳍条长度和等鳍面面积两种情况下, 仿生鳍波动产生的平均推进力随鳍条倾角的变化规律, 同时测量了鳍条倾角为45°时不同运动学参数下两种模式的推进力. 得出以下结论:
1) 在等鳍条长度条件下, 平均推进力随着鳍条倾角的增大而增加; 在等鳍面面积条件下, 平均推进力随着鳍条倾角增大而减小. 且相同条件下, 等鳍面面积仿生鳍产生的平均推进力始终大于等鳍条长度情况.
2) 在同一倾角下, 两种情况的平均推进力均随着频率、 摆幅和波长的增加而增大, 且这种变化趋势总体一致. 同样, 无论哪种运动学参数, 等鳍面面积仿生鳍产生的平均推进力均大于等鳍条长度仿生鳍产生的推进力.
3) 在等鳍条长度情况下, 仿生鳍上下表面压力差随着倾角的增加而增大; 在等鳍面面积情况下, 随着鳍条倾角的增大, 正负压力差随之减小, 计算区域内流场的涡街强度亦减弱. 而仿生鳍运动产生的上下表面压力差、 尾涡强度和分布形式以及迎水面面积等因素被认为是等鳍条长度与等鳍面面积仿生鳍平均推进力存在差异的主要原因.
(4) 根据研究结果, 对于仿生鱼鳍结构优化而言, 在一定鳍面面积下, 应尽量减小鳍条与根部固定底座之间的夹角, 从而提高推进力.
[1]Krylov V V, Pritchard G. V. Experimental confirmation of the propulsion of marine vessels employing guided flexural waves in attached elastic fins[J]. Journal of Fluids and Structures, 2007, 23, 297-307.
[2]Sfakiotakis M, Lane D M, Davies B C. An experimental undulating-fin device using the parallel bellows actuator[C]. Proceedings of the 2001 IEEE International Conference on Robotics and Automation. Seoul, Korea, 2001: 2356-2362.
[3]Alvarado P V, Chin S, Larson W, et al. A soft body under-actuated approach to multi degree of freedom biomimetic robots: a stingray example[C]. 3rd IEEE RAS and EMBS International Conference on Sept. 2010: 473-478.
[4]刘芳芳, 杨灿军, 苏琦, 等. 仿生鱼鳍运动仿真分析及试验研究[J]. 机械工程学报, 2010, 46(19): 24-29. Liu Fangfang, Yang Canjun, Su Qi, et al. Simulation analysis and experimental research on the movements of biomimetic fin[J]. Journal of Mechanical Engineering, 2010, 46(19): 24-29. (in Chinese)
[5]Low K H. Modelling and parametric study of modular undulating fin rays for fish robots[J]. Mechanism and Machine Theory, 2009, 44: 615-632.
[6]Shirgaonkar A A, Curet O M, Patankar N A, et al. The hydrodynamics of ribbon-fin propulsion during impulsive motion[J]. The Journal of Experimental Biology, 2008, 211: 3490-3503.
[7]Hu T J, Shen L C, Lin L X, et al. Biological inspirations, kinematics modeling, mechanism design and experiments on an undulating robotic fin inspired by Gymnarchus niloticus[J]. Mechanism and Machine Theory, 2009, 44: 633-645.
[8]Tangorra J, Anquetil P, Fofonoff T, et al. The application of conducting polymers to a biorobotic fin propulsor[J]. Bioinsp. and Biomim, 2007, 2: S6-S17.
[9]Clark R P, Smits A J. Thrust production and wake structure of a Batoid-inspired oscillating fin[J]. Journal of Fluid Mechanics, 2006, 562: 415-429.
[10]Kalumuck K M, Brandt A, Armand M, et al. Biomimetic undulating fin propulsion for maneuvering underwater vehicles[J]. Johns Hopkins Apl technical Digest, 2010, 28(3): 278-279.
[11]Ayers J, Westphal A, Blustein D. A conserved neural circuit-based architecture for ambulatory and undulatory biomimetic robots[J]. Marine Technology Society Journal, 2011, 45(4): 147-152.
[12]Boileau R, Fan L, Moore T. Mechanization of rajiform swimming motion: the making of robo-ray[D]. Vancouver: University of British Columbia, 2002.
[13]Wang Z L, Hang G R, Li J, et al. A micro-robot fish with embedded SMA wire actuated flexible biomimetic fin[J]. Sensors and Actuators, 2008, 144: 354-360.
[14]Zhang Y H, He J H, Zhang G Q. Biomimetic undulatory robotic fin optimization design using computational fluid dynamic method[C]. CSO, 2011 Fourth international joint conference on computational sciences and optimization, 2011: 51-55.
[15]Punning A. A biologically inspired ray-like underwater robot with electroactive polymer pectoral fins[J]. IEEE Mechatronics and Robotics (MechRob'04). Aachen, 2004(20): 241-245.
[16]Takagi K. Development of a Rajiform swimming robot using Ionic Polymer artificial muscles[C]. Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. San Diego, California, USA, 2006: 1861-1866.
[17]Lighthill J, Blake R. Biofluiddynamics of balistiform and gymnotiform locomotion. Part 1. Biological background and analysis by elongated-body theory[J]. Journal of Fluid Mechanics, 1990, 212: 183-207.
[18]Blake R W. The swimming of the mandarin fish synchropus picturatus[J]. J. Marine Biol. Assoc., 1979, 59: 421-428.
[19]Jagnandan K, Sanford C P. Kinematics of ribbon-fin locomotion in the bow fin Amia calva[J]. J. Exp. Zool. 2013, A319: 569-583.
[20]Youngerman E D, Flammang B E, Lauder G V. Locomotion of free-swimming ghost knife fish: anal fin kinematics during four behaviors[J]. Zoology, 2014, 117: 337-348.
[21]Daniel T L. Forward flapping flight from flexible fins[J]. Canadian Journal of Zoology, 1988, 66: 630-638.
[22]Hu T J, Shen L C, Gong P L. CFD validation of the optimal arrangement of the propulsive dorsal fin of gymnarchus niloticus[J]. Journal of Bionic Engineering, 2006(3): 139-146.
[23]Zhang Y H, Song Y, Yang J, et al. Numerical and experimental research on modular oscillating fin[J]. Journal of Bionic Engineering, 2008, 5(1): 13-23.
[24]Zhang Y H, He J H, Yang J. A computational fluid dynamics (CFD) analysis of undulatory mechanical fin driven by shape memory alloy[J]. International Journal of Automation and Computing, 2006, 3(4): 374-381.
[25]Wen L, Lauder G V. Understanding undulatory locomotion in fishes using an inertia compensated flapping foil robotic device[J]. Bioinspir Biomim, 2013, 8: 046013.
[26]Quinn D B, Lauder G V, Smits A J. Maximizing the efficiency of a flexible propulsor using experimental optimization[J]. J. Fluid Mech., 2015, 767: 430-448.
[27]Krishnamurthy P, Khorrami F, Leeuw J, et al. An electric ray inspired biomimetic autonomous underwater vehicle[C]. 2010 American Control Conference Marriott Waterfront, Baltimore, MD, USA, 2010: 5224-5229.
[28]He Jianhui, Zhang Yonghua, Low Kinhuat. Comparative study of effect of fin arrangement on propulsion performance of bio-inspired underwater vehicles with multiple SMA fins[J]. International Journal of Advanced Robotic System, 2015, 12: 1-15.
Influence of Ray Angle of a Biomimetic Fin on Its Thrust Generation
ZHANG Yong-hua
(College of Mechatronic Engineering, Taizhou Vocational and Technical College, Taizhou 318000, China)
In order to investigate the influence of fin ray angle on thrust generation of a biomimetic undulating fin, kinematic modeling and hydrodynamic modeling were established. Based on experimental technology, the change of thrust with fin ray angles 30°, 40°, 45°, 50°, 60°, 70°, 80° and 90°) under the two conditions (constant fin ray length and constant fin surface area) were illustrated. The thrust at fin ray angle of 45° with different kinematic parameters under the two conditions were also measured. A preliminary explanation on the cause of those differences was conducted according to the theory of computational fluid dynamics (CFD). The results indicate that: in the case of the constant fin ray length, the averaged propulsion thrust increases with the increase of angle of fin ray; in the case of the constant fin area, the averaged thrust decreases with the increase of angle of fin ray. However, the averaged thrust in the case of the constant fin area is always larger than the case of the constant fin ray length at the same condition. The results provide some useful references for optimal structure design of biomimetic undulating fin based propulsor.
undulating fin; fin ray inclination; thrust; computational fluid dynamics
1673-3193(2016)06-0606-08
2016-03-04
浙江省自然科学基金资助项目(LY15E060001); 台州职业技术学院一般课题(2017YB01)
章永华(1980-), 男, 副教授, 博士, 主要从事仿生机器人方面的研究.
TP242
A
10.3969/j.issn.1673-3193.2016.06.010
