低载波比工况下永磁同步电机磁链矢量轨迹分析

沈建新，何 标

(浙江大学 电气工程学院 浙江省电机系统智能控制与变流技术重点实验室，杭州 310027)

0 引 言

永磁同步电机无论是工作在电动机模式还是发电机模式，都可以采用空间矢量脉宽调制(SVPWM)控制。在每个PWM周期，都会给电机施加一个具有适当模值、相位和作用时间的目标电压矢量。目标电压矢量对时间的积分可以产生磁链矢量。通常情况下，电机的每个基波周期内包含多个PWM周期，因此电压矢量的积分会产生一个多边形的磁链矢量运行轨迹(以下简称磁链轨迹)，接近于圆形轨迹，进而形成接近于圆形轨迹的电流矢量，使得电机的相电流波形为正弦形，由此可以实现良好的矢量控制。

当永磁同步电机高速运行时，基波频率提高，而变流器的开关频率是有限的；或者，当永磁同步电机的功率很大，虽然基波频率并不一定高，但是变流器的开关频率因功率大而显著减小。这两种情况下，都会使得载波比(即PWM频率与电机基波频率之比)减小[1]，甚至可能小于6。

理想情况下，SVPWM控制产生的多边形磁链轨迹的边数就是载波比的值。显然，在低载波比工况下，磁链轨迹远远偏离圆形，使得电流矢量的轨迹也偏离圆形，即电机的相电流波形发生畸变，矢量控制的性能也会恶化。

文献[2]针对低载波比问题提出四种解决方法：(i)用若干串并联的功率器件代替一个功率开关，这些器件的轮流动作来等效实现更高的开关频率[3]；(ii)采用多电平模块化变流器(MMC)来改善电机电压的波形；(iii)采用三相开绕组电机结构，从而获得更多的可供选择的基础电压矢量来合成目标电压矢量；(iv)与第(iii)种方法类似，采用双三相结构产生更多的基础电压矢量，由此可以更好地合成目标电压矢量，进而获得更好的磁链轨迹的圆度。本文将对常规三相(简称单三相)以及双三相永磁同步电机的电压矢量合成、磁链轨迹特性进行对比研究，分析双三相电机磁链轨迹具有更好圆度的机理，为采用双三相结构改善低载波比工况下的控制性能提供理论依据。

1 数学模型

建立数学模型时，基于如下假设条件：气隙磁场为正弦分布，电枢绕组电感随转子位置呈正弦型变换规律，不考虑磁路饱和、铁心损耗。

对于单三相电机而言，可以用式(1)的变换矩阵C3s/2s实现各个变量从a-b-c坐标到α-β-0坐标的变换(α轴与a轴重合)，用式(2)的变换矩阵C2s/2r实现从α-β坐标到d-q坐标的变换。其中θ是转子d轴与定子α轴的夹角。一般而言，0轴分量不参与机电能量转换，且在绕组星形连接而中心点不引出时的电流0轴分量为0，因此一般不予考虑。

(1)

(2)

定子绕组中的电压、电流、磁链在α-β坐标和d-q坐标下均可以表示为矢量，即：

(3)

三相电机在α-β平面的电压方程为

(4)

式中,Rs为定子绕组电阻。由式(3)、式(4)可知电压方程也可写成矢量表达式：

(5)

三相电机在d-q平面的电压、磁链方程分别为

(6)

(7)

式中,Ld、Lq分别为d、q轴电感，ω转子电角速度，ψm为永磁体在电枢绕组中的励磁磁链幅值(视作常数)。

由式(7)可知，若d-q平面的磁链分量为常数，则电流分量也为常数，那么在a-b-c坐标下，电机的相电流ia、ib、ic随转子位置的变化就呈理想的正弦波。很显然，此时的磁链矢量、电流矢量的模值均不变，而其相位角随转子位置而变化，因此，磁链、电流矢量的运行轨迹均为理想的圆形。因而，单三相永磁同步电机基于SVPWM的矢量控制，就是要将实际的磁链轨迹调制得尽可能呈圆形。另一方面，从式(6)可知，d-q平面的电压分量也随之成为常数，即理想的电压矢量的运行轨迹也是圆形。

双三相电机由A、B、C和D、E、F两套三相绕组组成，D相绕组相对A相绕组空间相移30电角度，两套绕组各自Y型连接且中性点相互隔离，如图1所示。

图1 双三相永磁同步电机系统

双三相电机按式(8)中的变换矩阵C6s/2s实现从A-B-C-D-E-F到α-β-z1-z2-01-02的坐标变换[4]，α轴与A轴重合。这里的α-β正交平面与单三相电机坐标变换后的α-β平面一致；从α-β坐标到d-q坐标的变换矩阵同式(2)，其中θ仍然是转子d轴与定子α轴的夹角；各变量的矢量表达式同式(3)，电压表达式同式(4)～(6)，而磁链表达式如式(9)所示，即d轴和q轴电感的大小有所不同；α-β平面或d-q平面的相关变量参与机电能量转换。z1-z2正交平面的分量对应电机各变量的谐波分量，在正弦型的永磁同步电机中不产生有效电磁转矩，故暂不考虑。01-02正交平面表示0分量，故一般也不作考虑。

(8)

(9)

很显然，双三相永磁同步电机基于SVPWM的矢量控制也要将磁链轨迹调制得尽可能呈圆形。

2 基于SVPWM的矢量控制

将式(5)改写为积分形式：

(10)

式中的电压矢量代表电机的外施电压。永磁同步电动机由逆变器供电，或者，永磁同步发电机通过PWM整流器对外输出直流电，因此，电机的相电压是脉冲波而不是正弦波。换言之，电压矢量的运行轨迹不是理想的圆形。通常外施电压远大于电阻压降。在SVPWM控制下，在每个PWM周期内只施加一个目标电压矢量，因此式(10)可进一步简化为

(11)

式中,T为PWM周期。所以，基于SVPWM的矢量控制，可使得磁链矢量按式(10)逐步变化；只要目标电压矢量选择合适，就可以使磁链矢量的运行轨迹呈现一个多边形。这个多边形的边数就是载波比的数值。因此，载波比足够高时，多边形的磁链轨迹接近于圆形，由此达到矢量控制的目的。

然而，目标电压矢量也不是变流器可以直接产生的，而是需要通过基础电压矢量合成。

2.1 单三相电机SVPWM矢量控制

对于单三相电机，基础电压矢量为

(12)

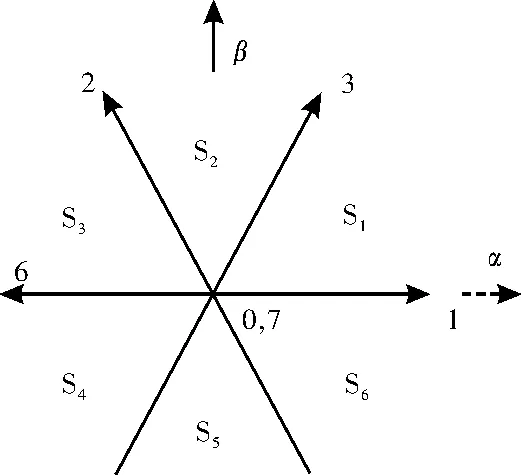
图2 单三相电机基础电压矢量图

例如，若矢量控制需要施加在电机上的目标电压矢量落在S1扇区，则由1号和3号基础电压矢量及零矢量按式(13)合成该目标矢量，其中零矢量可以是0号，也可以是7号。若采用中心对称的七段式调制法，则变流器的PWM状态如图3所示。

(13)

图3 单三相电机SVPWM在S1扇区的开关状态

2.2 双三相电机SVPWM矢量控制

双三相电机的基础电压矢量为

(14)

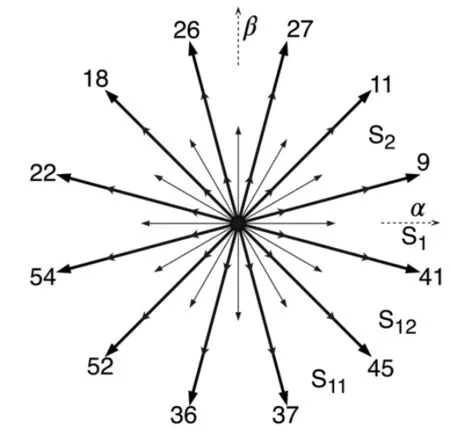
图4 双三相电机基础电压矢量图

与单三相电机的SVPWM矢量控制类似，双三相电机的目标电压矢量也由基础矢量合成。很显然，在双三相电机中，有更多的基础矢量可供选择，扇区划分也更精细，因此有望使磁链轨迹更加接近于圆形。通常只选用模值最大的12个基础电压矢量，则α-β平面共有12个扇区；目标电压矢量由划定其所在扇区的两个基础矢量合成，即为最大二矢量法。例如，扇区S1内的目标电压矢量可以由41号和9号基础矢量合成，采用中心对称的七段式调制法时，变流器的开关状态如图5所示。

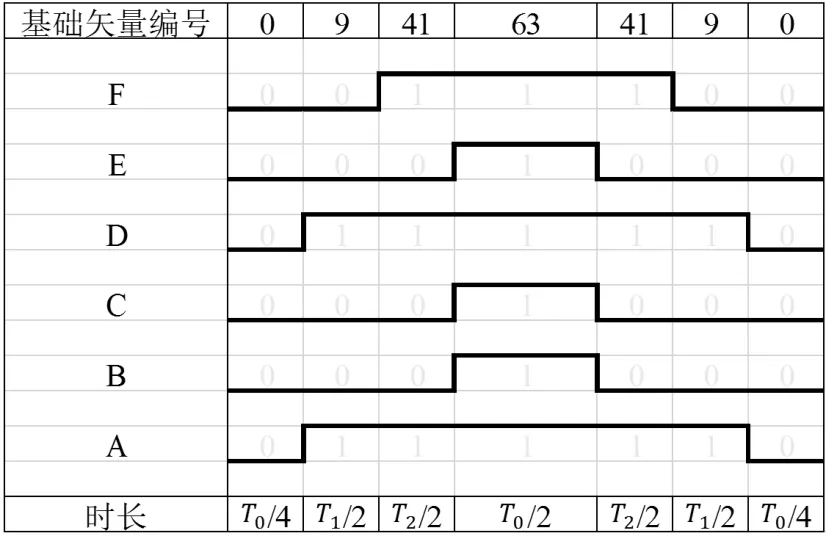
图5 双三相电机SVPWM在S1扇区的开关状态

3 低载波比工况下磁链矢量运行轨迹

载波比决定了一个基波电周期内目标电压矢量的个数，即为斩波次数。若载波比为整数N，稳态时磁链轨迹为正N边形，因此载波比数值越大，磁链轨迹越接近于理想圆形。而目标电压矢量是由基础矢量合成的，因此，采用中心对称的七段式调制法时，所谓N边形的每条边其实是由三条折线合成的。当然，实际的载波比不一定为整数。

当载波比很低时，磁链轨迹显然会远远偏离圆形。以永磁同步电机基波频率550Hz、PWM载波频率2.5kHz为例，载波比低至4.55。此时单三相和采用最大二矢量法的双三相电机的磁链轨迹如图6所示。图中给出了5个PWM周期内的磁链轨迹。图中各个实线箭头的方向表示基础电压矢量的相位，其长度代表基础电压矢量的作用时间。图中并未标出磁链矢量。磁链矢量的箭尾始终落在圆心。随着磁链矢量的运动(即随着磁链矢量相位的变化)，其模值一直在发生变化而不是期望的常数，其运行轨迹就是图中的箭头所构成的多边形而不是圆形。换言之，磁链矢量的箭头落在多边形上。可见，在低载波比工况下，单三相和双三相电机的磁链轨迹均严重畸变，但它们的平滑度有所不同。

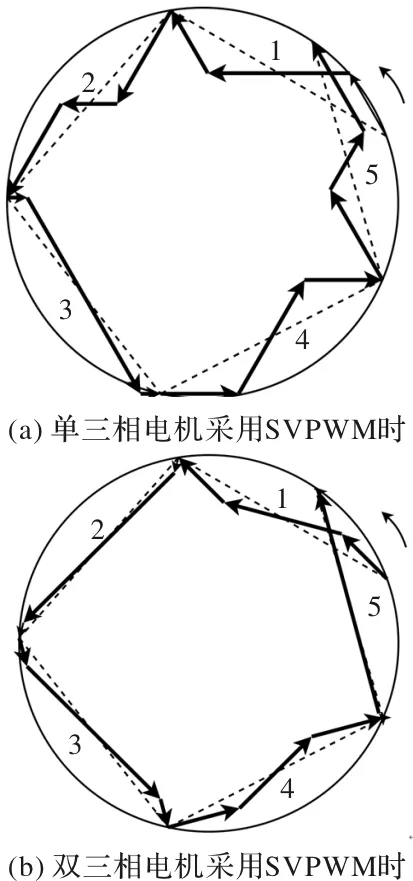
图6 低载波比时磁链矢量运行轨迹示意图

为了对磁链轨迹的优劣进行评估，引入曲线圆度的定义。以轨迹上离圆心最小的距离作为轨迹内接圆的半径(如图7中的r1所示)，以轨迹上离圆心最大的距离作为轨迹外接圆的半径(见图7中的r2)，用轨迹外、内接圆的半径差和理想磁链圆半径(图7中的r0)的比值来描述曲线的圆度，该值越小表示磁链轨迹越接近于圆形。

采用中心对称的七段式SVPWM调制法时，在一个PWM周期内目标电压矢量由三段矢量合成，因此，如图7所示，其中第一、三段属于同一基础矢量，第二段属于另一个基础矢量。显然，由于两种电机的基础电压矢量的个数以及扇区的划分不同，单三相电机的两个相邻基础矢量相差60电角度，而双三相电机的两个相邻基础矢量相差30电角度。从图中可以看出，单三相电机的磁链轨迹比双三相电机具有更大的“波折”程度，因此圆度较差。

图7 磁链轨迹圆度示意图

本文对相同功率、电压、转速、极数的单三相和双三相永磁同步电机进行仿真，电机参数如表1所示。两台电机均做发电机运行，基波频率为550Hz，为了输出200V直流电压，均采用弱磁控制。当PWM整流器的载波比分别为4.55和9.09时，仿真可得磁链轨迹的圆度值分别为39.3%(单三相)和28.6%(双三相)，以及20.3%(单三相)和13.8%(双三相)。仿真结果如图8所示，清晰表明：随着载波比的降低，两种电机的磁链轨迹畸变均趋于严重，但是双三相电机始终优于单三相电机。

由此可见，在低载波比工况下，采用SVPWM矢量控制时，双三相永磁同步电机比单三相电机具有更灵活的目标电压合成手段，因此所得到的磁链矢量运行轨迹也具有更好的圆度，有利于改善矢量控制的性能。

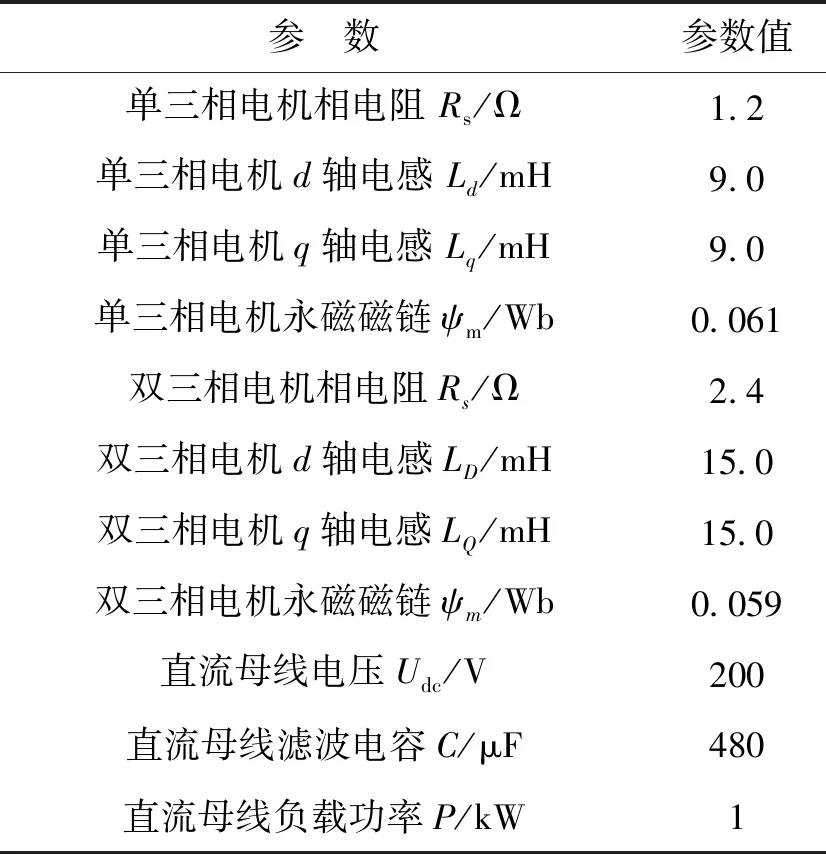
表1 永磁同步电机PWM整流系统参数

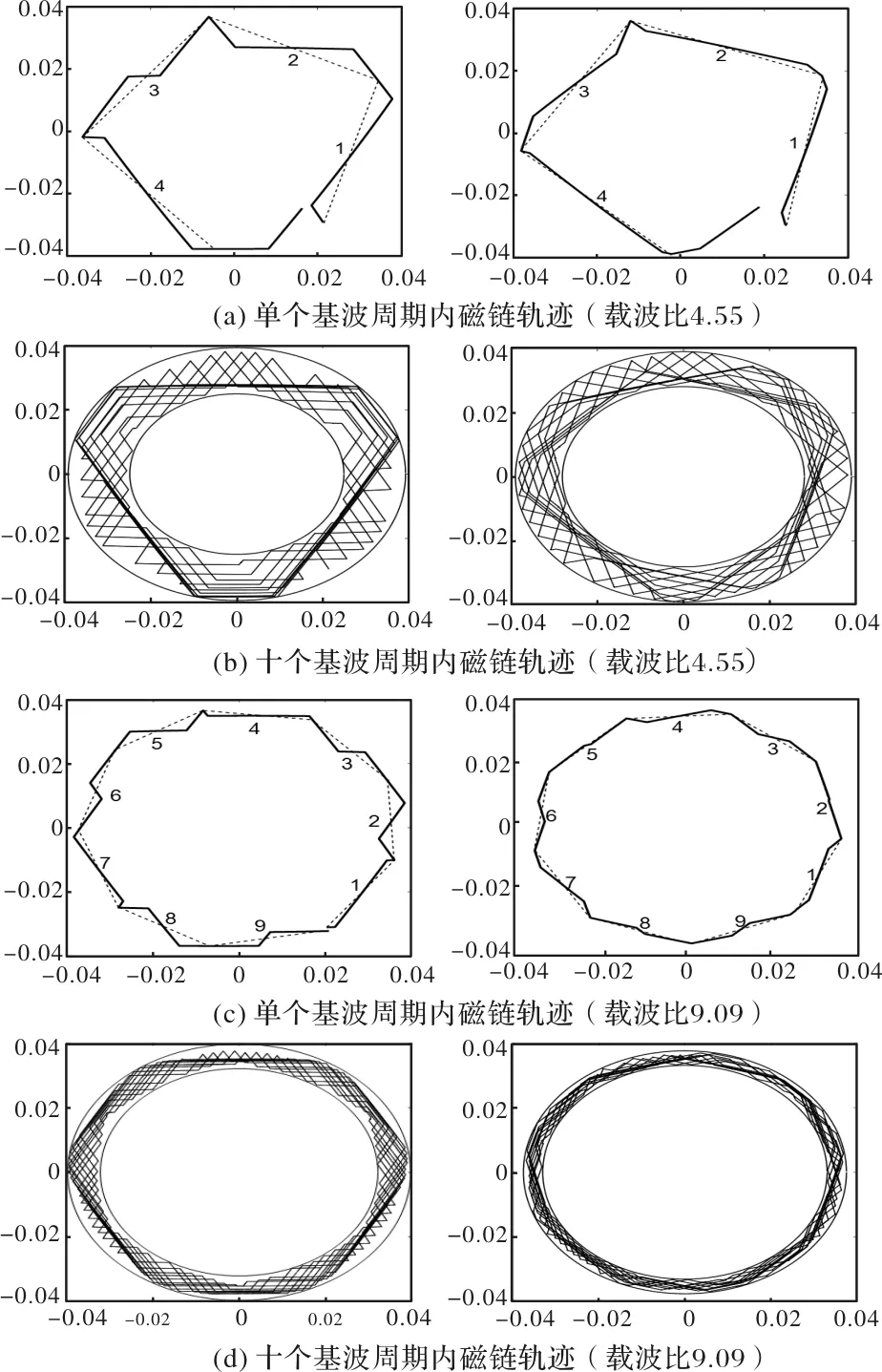
图8 磁链矢量运行轨迹圆度仿真结果(左：单三相电机，右：双三相电机)

4 结 语

由理论分析和仿真结果可知，在低载波比工况下，SVPWM所合成的磁链矢量运行轨迹偏离理想的圆形，使得永磁同步电机的矢量控制性能变差。相比于单三相电机，双三相电机SVPWM控制系统拥有更多的可供选择的基础电压矢量，且扇区更加细化，因此气隙磁链矢量运行轨迹有相对较好的圆度，有利于解决低载波比带来的问题。

当然，采用最大二矢量法时，双三相电机只用了12个非零基础电压矢量。如果将其他48个非零矢量部分或全部利用起来，就可能把扇区进一步细分到24个。此外，在低载波比工况下，如果一个PWM周期内的变流器开关信号采用不对称波形，有望使磁链矢量更接近于沿着理想的圆形运行，而不是沿着由目标电压矢量简单积分所得的多边形运行。因此，今后将对双三相电机的SVPWM矢量控制开展更加深入的研究，以期进一步改善控制性能。