Q245R钢非线性超声特性与晶粒度级别量化关系研究

徐 磊，张 颖，朱子东，刘 识，张 潇

(1.东北石油大学机械科学与工程学院,黑龙江 大庆 163318；2.常州大学环境与安全工程学院，江苏 常州 213164；3.沈阳龙昌管道检测中心，辽宁 沈阳 110168 )

0 引言

大多数压力容器的失效与故障，是由于长期作业、高压情况下工作而引起的材料晶粒尺寸改变所致。常规无损检测方法如衰减法、反射法等对于材料内部复杂的多晶状态检测具有一定的局限性[1-3]。因此，找出有效的检测方式来研究材料内部晶粒度级别变化，尤其是晶粒级别极高时的裂纹与缺陷，进行特种设备的早期探伤与危险预防具有重要的研究意义。非线性超声技术是应用高频波在介质中传递，与材料内部微观缺陷相互作用，通过对一次谐波、二次谐波等参数的分析，实现材料性能评价以及微观缺陷检测等目的[4]。研究表明，基于位错模型的非线性超声参量与材料内部晶粒度级别以及位错密度有很强的相关性，使得建立晶粒度级别与非线性超声参量的量化关系成为可能[5-8]。

近年来，国内外学者利用非线性超声检测技术对材料晶粒尺寸进行研究，发现材料晶粒尺寸对材料的力学性能影响很大。周正干等[9]利用非线性超声技术，研究镍基高温合金GH706的微观结构，发现当GH706合金硬度强化的主要原因为时效强化时，非线性超声特性与时效强化存在很强的相关性，证明非线性超声特性可以识别GH706合金内部晶格错配程度。黄雨晴等[10-12]关于晶粒尺寸的研究也证明了金属材料的各项力学性能都与其微观状态有关。Marino等[13]对不同老化阶段的马氏体钢进行非线性超声实验，发现相对非线性参数对马氏体不同晶粒度级别的位错密度变化敏感，证明了可以利用非线性超声技术判断材料老化过程中晶粒尺寸的变化。本文运用RITEC RAM-5000 SNAP仪器，对不同晶粒度级别的Q245R钢试件进行非线性超声技术检测，建立了Q245R钢非线性特性与晶粒度级别的定量关系。证明了通过非线性系数可以判断Q245R钢材料晶粒度级别。

1 非线性超声特性计算理论基础

1.1 二阶非线性系数

研究表明，固体介质特别是金属都具有传导超声波的性质，单频正弦超声波能够在固体介质中经过连续的互相作用产生相应的因子，激发高频谐波[14]。

Cantrell等[15]通过对固体介质非线性特性的研究，建立了非线性超声波动方程：

(1)

应用微扰理论可求得式(1)的近似解为

(2)

ρ0为被测介质密度；x为超声波传播的距离；t为超声传导的试件；u为被测介质内位于x处质点的位移；K2为二阶弹性常数；K3为三阶弹性系数；k为波数；A0为声波初始幅度。

依据式(2)可得材料的二阶非线性系数为

(3)

A1为基波幅值(声波初始幅值)；A2为二次谐波幅值；β为二阶非线性系数。

实验过程中，通过RITEC RAM-5000 SNAP仪器发射的超声波频率与被测试件本身的长度是保持不变的[16]，即

(4)

1.2 衰减系数

超声波在介质中传递的过程中会产生衰减，本文通过对信号振幅的损失作为衰减程度的计算标准，计算衰减系数：

(5)

α为衰减系数；U1为一次反射回波幅值；U2为二次反射回波幅值；x1-x2为被测试件厚度。

2 试件制备及实验方案

2.1 试件制备

实验选取Q245R钢作为实验试件，详细尺寸如图1所示。为了确保声波能不受干扰地准确传导，厚度设计为12 mm。

图1 实验试件规格

2.2 实验方案

本实验对不同晶粒度Q245R钢试件进行非线性超声检测实验。通过实验得到试件的非线性超声特性参数，从而分析材料不同晶粒度对非线性超声特性的影响。建立非线性超声特性与Q245R钢晶粒度大小之间的关系，通过非线性超声特性判断Q245R钢内部晶粒度等级。非线性超声检测系统如图2所示。

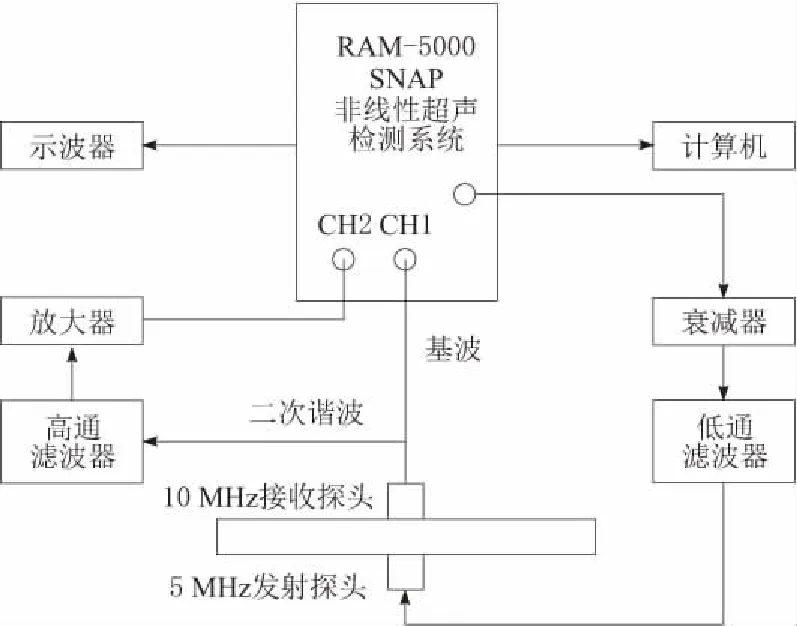
图2 非线性超声检测系统

为了实验的整体性与后期分析，首先对8个经过机械轧制而成的试件，编号S1～S8，然后通过不同的热处理技术加工8个试件，使之内部晶粒度区分为4组级别，利用4种热处理方式分别制备2个试件。其热处理工艺如表1所示。选取1～6号砂纸依顺序对试件进行打磨并抛光，配置硝酸酒精溶液对抛光后的试件进行侵蚀，利用专业金相显微镜，观察试件放大500倍后的金相，拍摄金相图，通过金相图中晶粒个数，计算试件晶粒度级别。不同热处理加工后的试件金相图如图3所示。最后，利用RITEC系统对热处理加工后的8个实验试件进行非线性特性计算，包括二阶非线性系数、衰减系数、超声波在试件内传递的声速。利用计算得到的材料晶粒度级别，分析4组实验试件非线性超声特性的相关性。

表1 Q245R钢热处理工艺与预测晶粒度级别

图3 不同热处理后4种晶粒级别Q245R钢金相图(放大500倍)

3 Q245R钢不同晶粒度非线性超声特性分析

3.1 二阶非线性系数测量与计算

利用美国RITEC非线性超声测试系统，通过频率为5 MHz的发射探头将超声波打入Q245R钢试件中，并通过频率为10 MHz的接收探头将超声波信号传输回系统中。通过系统连接的示波器，可以看到如图4和图5所示基波与二次谐波的图像。

图4 基波波形

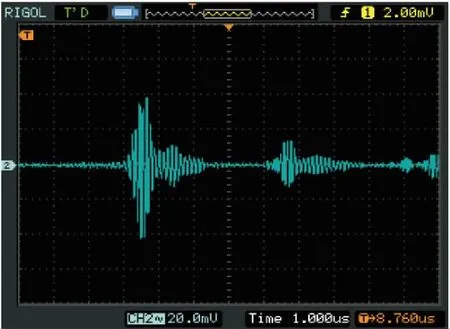
图5 二次谐波波形

通过系统选出的算法门限范围对示波器显示的波形进行运算，在5 MHz频率位置上得到基波的幅值A1，在10 MHz的二倍频率位置上得到二次谐波幅值A2。利用非线性系数公式，计算出不同晶粒度级别Q245R钢二阶非线性系数如表2所示。

表2 8个试件的二阶非线性系数

3.2 衰减系数与声速的测量与计算

利用美国RITEC非线性超声测试系统，采用反射法测量不同晶粒度Q245R钢试件的衰减系数与声速。将正弦脉冲波通过5 MHz的发射探头打入Q245R试件中，声波在通过反射后回到探头中，通过衰减系数公式(5)测量得到不同晶粒度级别Q245R钢试件衰减系数，如表3所示。通过非线性超声实验系统，测量得到的不同晶粒度级别Q245R钢试件声速在5 950 m/s左右，且波动很小。

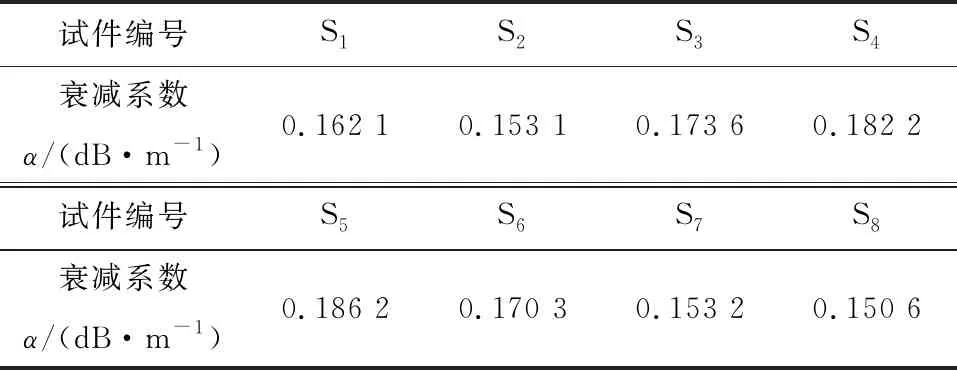
表3 8个试件的衰减系数

3.3 Q245R钢试件晶粒度级别计算

为了确定热处理加工后每个试件的准确晶粒度级别，使测量得到的相关非线性超声特性与试件晶粒度级别相对应，采用面积法测量计算本次实验的晶粒度级别。在金相图放大100倍的情况下，在645.16 mm2面积内包含的晶粒个数N与晶粒度级别数G的关系为

N=2G-1

(6)

由式(6)计算图3中晶粒个数，得到Q245R钢试件4种晶粒度级别如表4所示。

表4 8个试件晶粒度级别

3.4 结果分析

Q245R钢的不同晶粒度级别的声速与衰减系数关系如图6所示。由图6可知，随着Q245R钢晶粒度级别增大，超声波在试件中的声速变化不大，其最大声速与最小声速相对变量只有2.62%，而衰减系数随晶粒度级别的变化相对于声速更加明显，相对变量为19.1%。在晶粒度级别达到4.35之前，衰减系数随变量上升，之后呈小幅度下降。

不同晶粒度级别Q245R钢试件二阶非线性系数如图7所示。由图7可知，随着晶粒度级别等增大，二阶非线性系数呈线性下降，超声非线性效应随着晶粒度级别的增大而降低得比较明显，并且具有很强的相关性，近似于线性表征。Q245R钢晶粒度级别增大，内部晶粒变小，超声导波需要穿过的晶界面积相应增大，接收探头接收到的超声导波幅值随之呈比例减小，由非线性系数公式可知，二阶非线性系数相应减小。

根据实验所得非线性系数与不同试件晶粒度级别的相应关系，以及非线性系数折线(图7)，通过Origin软件计算分析，得到非线性系数与试件晶粒度级别存在线性关系为

β=-0.02x+0.174 6

(7)

x为晶粒度级别。

图6 声速与衰减系数折线

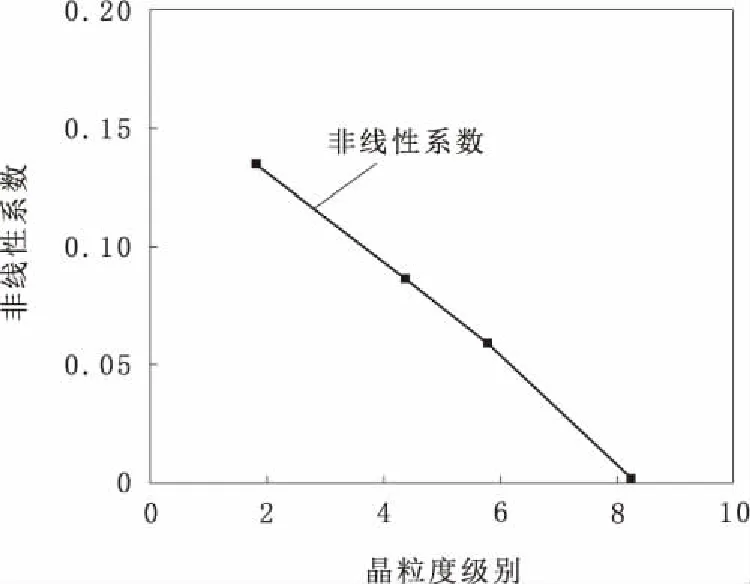
图7 非线性系数折线

4 结束语

通过对Q245R钢试件的非线性超声实验，计算了热处理后不同晶粒度级别的Q245R实验试件的3个非线性超声特性参数，通过定量分析，得到以下结论：

a.随着晶粒度级别的改变，Q245R钢的衰减系数发生了较大的相关性变化，表现为先升高后降低的趋势；声速的变化与试件晶粒度级别没有明显的相关性。

b.相比衰减系数与声速，Q245R钢试件的二阶非线性系数随着材料内部晶粒度级别的增大而减小，并且有明显的线性相关性。通过定量分析，得到式(7)所示的Q245R钢二阶非线性系数与晶粒度级别的线性拟合公式。

c.对Q245R钢试件进行的非线性超声实验，证明了存在一种确定的线性关系，可以将材料内部晶粒度级别与二阶非线性系数关联。

d.本文只针对Q245R钢进行了实验，分析得到的线性关系式(7)，不代表二阶非线性系数与其他金属材料晶粒尺寸的定量关系。